GMM / MoG 聚类 Matlab 可视化 实现

参考书籍：《计算机视觉 模型、学习和推理》

GMM介绍

我们知道，常规的正态分布或高斯函数只具有单峰形式，对于复杂的数据(如双峰或多峰)建模来说，很难实现较好的拟合效果。我们不妨设想，如果给予多个正态分布不同的权重 h_i , 并将它们线性叠加起来，是不是就可以来通过叠加后的分布来拟合比较复杂的数据了呢？

高斯混合模型 [ GMM(Gaussian Mixture Model), MoG(Mixture of Gaussians)] 就是这样的一个模型，通过叠加多个高斯来进行数据的拟合。

我们将权重 h_i 抽象成为一个分类分布Cat{1…K}, K是高斯函数的个数，那么观测到的数据 x 和 h_i 形成一个联合概率分布的边缘概率，在这里我们将h_i 看成一个隐变量(hidden variable/latent variable)。
$$\begin{array}{rl}Pr(x|h,\theta )& =Nor{m}_x[{\mu }_h,{\Sigma }_h]\\ Pr(h|\theta )& =Ca{t}_h[\lambda ]\end{array}$$

由上个公式我们可以看出，

1. 在给定 第h_i 个Gauss对应参数 θ{μ_k,Σ_k} 的情况下，此时观测变量就是一个正态分布。
2. 在我们参数已知的情况下，对应的 h_i 则是一个分类分布。
   下面这张图(摘自开篇参考书籍)形象化说明这两个公式：
   

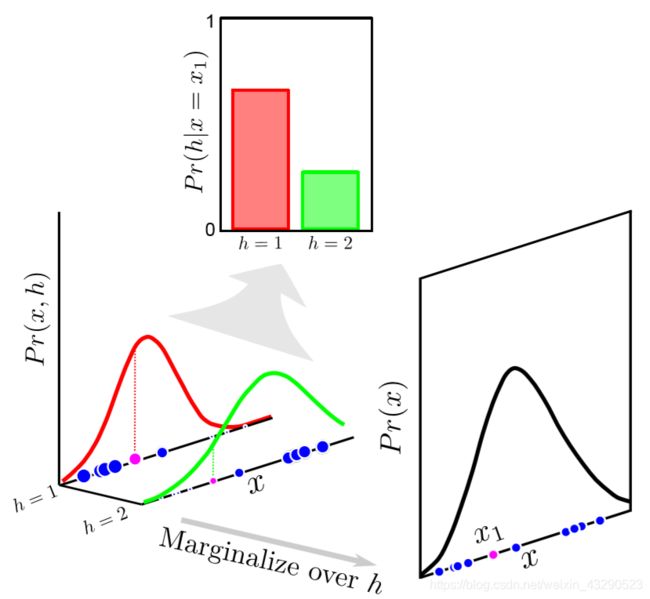
那么通过独立变量的联合概率和边缘概率乘积的关系，可以恢复原始的数据：

$$\begin{array}{rl}Pr(\mathbf{x}|\mathbf{\theta })& =\sum _{k=1}^{K}Pr(\mathbf{x},h=k|\mathbf{\theta })\\ & =\sum _{k=1}^{K}Pr(\mathbf{x}|h=k,\mathbf{\theta })Pr(h=k|\mathbf{\theta })\\ & =\sum _{k=1}^K{\lambda }_{k}Nor{m}_x[{\mathbf{\mu }}_k,{\mathbf{\Sigma }}_k]\end{array}$$

第一步，随机选取K个样本点，作为K个高斯函数的均值mu，整体数据的方差用来初始化K个高斯函数的方差sigma,每个高斯的权重初始化为1/K。

EM进行参数求解

如果我们直接对这多个高斯叠加而成的函数进行极大似然方法(MLE)来求解，一般来说很难求出闭式解：
$$\begin{array}{rl}& Pr(x)=\int Pr(\mathbf{x},\mathbf{h})d\mathbf{h}.\\ & \hat{\theta }=\underset{\theta }{\mathrm{argmax}}[\sum _{i=1}^I\log [Pr(x_i|\mathbf{\theta })]]\end{array}$$

所以如果我们通过引入一个分布简单的隐变量 h_i ，先求出它们联合概率分布，然后将隐变量 h_i 给积分掉，正如下面公式：
$$Pr(x|\theta )=\int Pr(\mathbf{x},\mathbf{h}|\mathbf{\theta })d\mathbf{h}.$$

然后对参数θ进行求解argmax(L), L是下面的对数似然函数，同样可以达到我们的目的:
$$\hat{\theta }=\underset{\theta }{\mathrm{argmax}}[\sum _{i=1}^I\log [\int Pr({\mathbf{x}}_i,{\mathbf{h}}_i|\mathbf{\theta })d{\mathbf{h}}_i]]$$

我们能不能构造一个下界函数(每一个点都小于或等于对数似然函数L)去逼近L:
$$\begin{array}{rl}B[\{q_i({\mathbf{h}}_i)\},\mathbf{\theta }]& =\sum _{i=1}^I\int q_i({\mathbf{h}}_i)\log [\frac{Pr(x_i,{\mathbf{h}}_i)}{q_i({\mathbf{h}}_i)}]d{\mathbf{h}}_i\\ & \le \sum _{i=1}^I\log [\int Pr(x_i,{\mathbf{h}}_i|\mathbf{\theta })d{\mathbf{h}}_i].\end{array}$$

证明如下：
由詹森不等式和Log函数的性质(凹函数)，可得E[log(x)]≤log(E[x])。
$$\begin{array}{rl}B[\{q_i(h_i)\},\theta ]& =\sum _{i=1}^I\int q_i(h_i)\log [\frac{Pr(x_i,h_i|\theta )}{q_i(h_i)}]d{h}_i\\ & \le \sum _{i=1}^I\log [\int q_i(h_i)\frac{Pr(x_i,h_i|\theta )}{q_i(h_i)}]d{h}_i\\ & =\sum _{i=1}^I\log [\int Pr(x_i,h_i|\theta )]d{h}_i\end{array}$$

上式B[…]又称为ELBO(证据下界)，其中 q_i(h_i) 就是给定 x_i, θ 条件下的分类分布概率： q_i(h_i) = Pr((h_i)|x_i, θ)。

在这里，我们使用EM(Expectation Maximization)算法来求解参数。

1. E-Step（固定θ，更新 q_i(h_i) 来提升ELBO）:
   求每个隐变量 h_i 的后验分布Pr(h_i|x_i)以最大化对应的分布 q_i(h_i) 的边界（根据贝叶斯法则）：
   $$\begin{array}{rl}{q}_i(h_i)=Pr(h_i=k|{\mathbf{x}}_i,{\mathbf{\theta }}^{[t]})& =\frac{Pr(x_i|h_i=k,{\theta }^{[t]})Pr(h_i=k,{\theta }^{[t]})}{{\sum }_{j=1}^{K}Pr(x_i|h_i=j,{\theta }^{[t]})Pr(h_i=j,{\theta }^{[t]})}\\ & =\frac{{\lambda }_{k}Nor{m}_{x_i}[{\mu }_k,{\Sigma }_k]}{{\sum }_{j=1}^K{\lambda }_{j}Nor{m}_{x_i}[{\mu }_j,{\Sigma }_j]}\\ & =r_{ik}.\end{array}$$这里的 r_k 称作对应关系(respoinsibility)。

2. M-Step（固定 q_i(h_i) ，更新 θ 来使得边界函数ELBO最大化）:
   在最大化这一步，对相应模型参数θ={λ_k,μ_k,Σ_k} 的边界进行最大化：

$$\begin{array}{rl}\hat{\theta }& =\underset{\theta }{\mathrm{argmax}}[\sum _{i=1}^I\sum _{k=1}^K{\hat{q}}_i(h_i=k)\log [Pr(x_i,h_i=k|\theta )]]\\ & =\underset{\theta }{\mathrm{argmax}}[\sum _{i=1}^I\sum _{k=1}^K{r}_{ik}\log [{\lambda }_{k}Nor{m}_{x_i}[{\mu }_k,{\Sigma }_k]]].\end{array}$$

最后，通过拉格朗日乘子法求解，可以得到更新法则：

$$\begin{array}{rl}{\lambda }_k^{[t+1]}& =\frac{{\sum }_{i=1}^I{r}_{ik}}{{\sum }_{j=1}^K{\sum }_{i=1}^I{r}_{ij}}\\ {\mu }_k^{[t+1]}& =\frac{{\sum }_{i=1}^I{r}_{ik}{x}_i}{{\sum }_{i=1}^I{r}_{ik}}\\ {\Sigma }_k^{[t+1]}& =\frac{{\sum }_{i=1}^I{r}_{ik}(x_i-{\mu }_k^{[t+1]})(x_i-{\mu }_k^{[t+1]}{)}^T}{{\sum }_{i=1}^I{r}_{ik}}\end{array}$$

GMM动态可视化

图1使用2个高斯拟合2个高斯随机生成的样本点集。
图2使用3个高斯拟合2个高斯随机生成的样本点集。

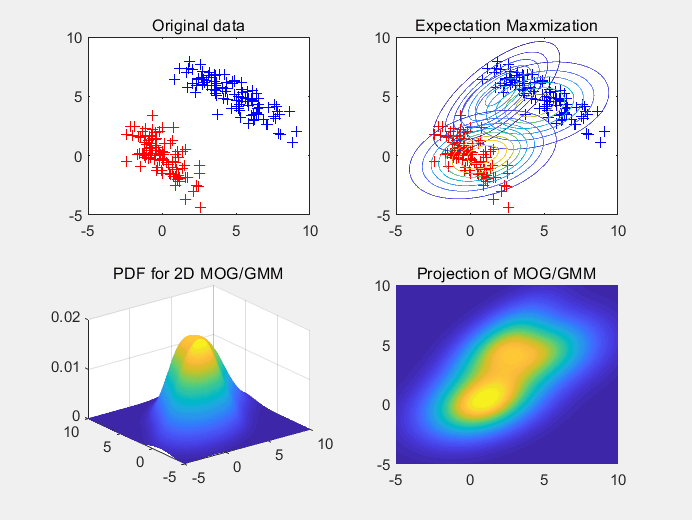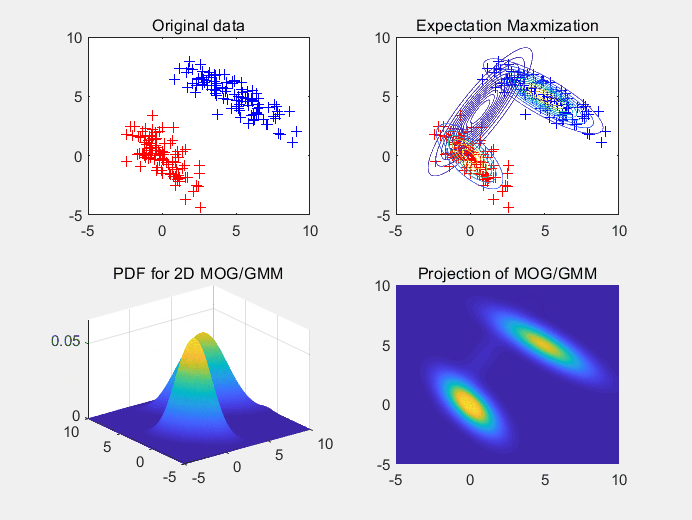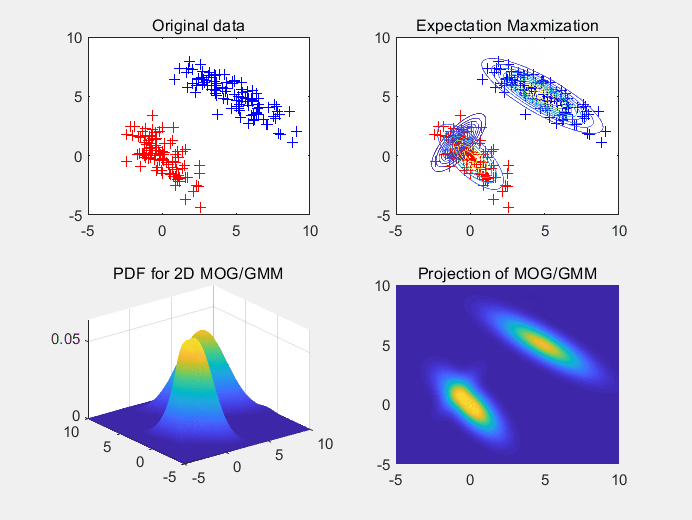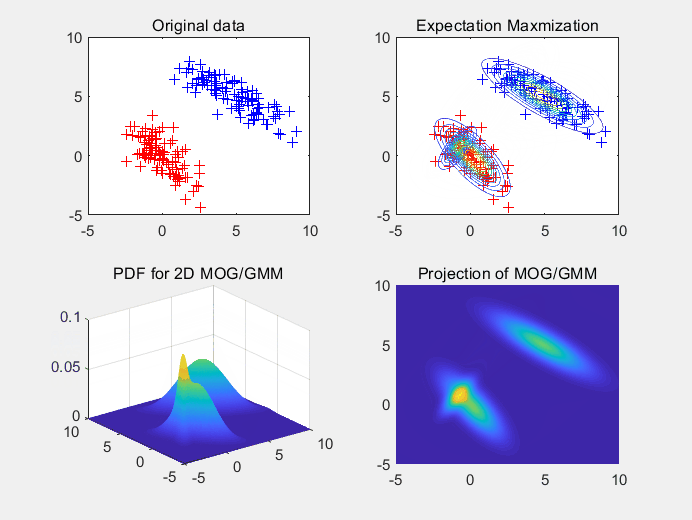
图3 使用3个高斯拟合3个高斯随机生成的样本点集。

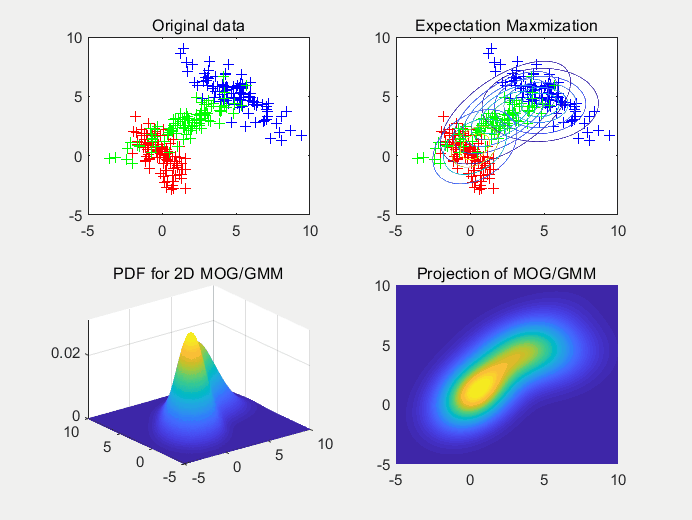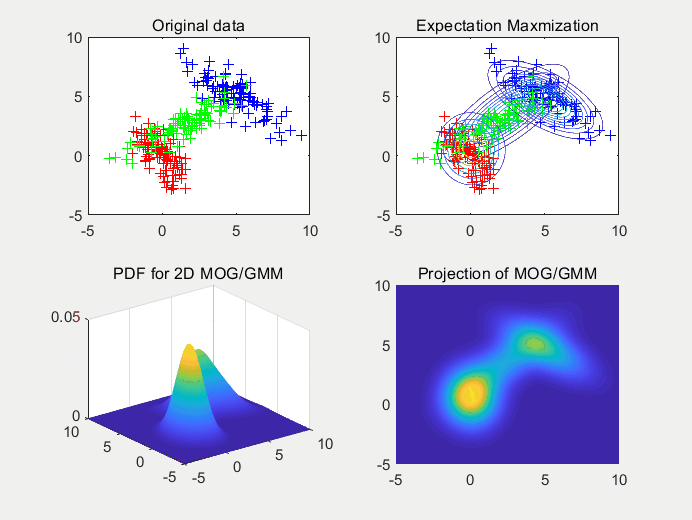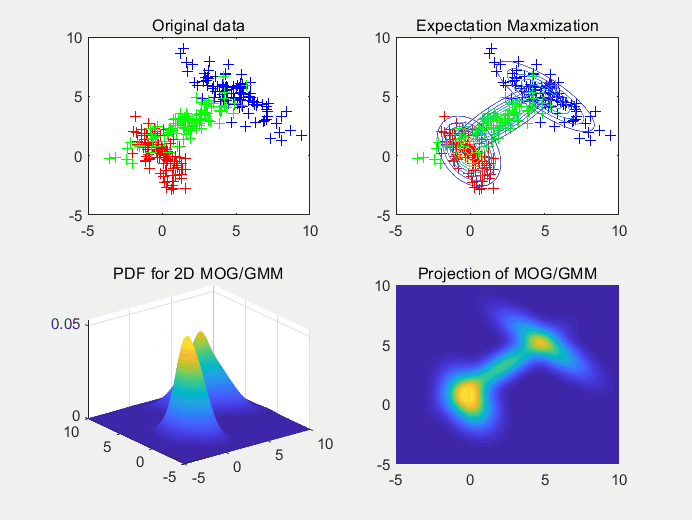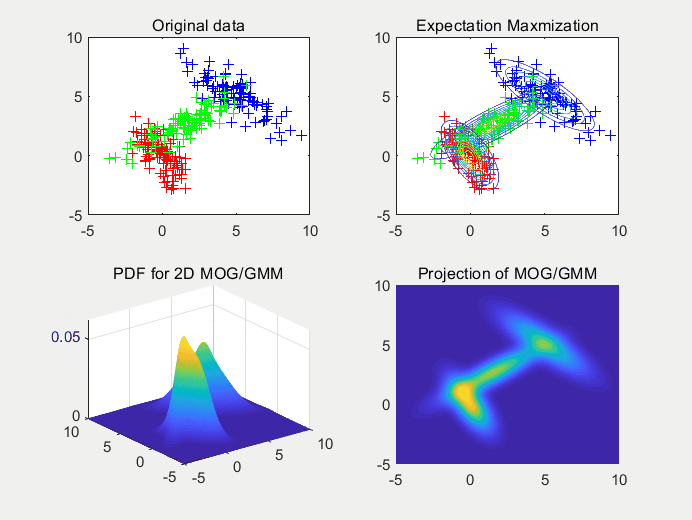
图4使用2个高斯拟合2个高斯随机生成的样本点集，在这里我们可以看出随机初始化的均值对拟合函数的收敛有影响。
图5使用3个高斯拟合3个高斯随机生成的样本点集，同样的，我们可以看出随机初始化的均值对拟合函数的收敛有影响。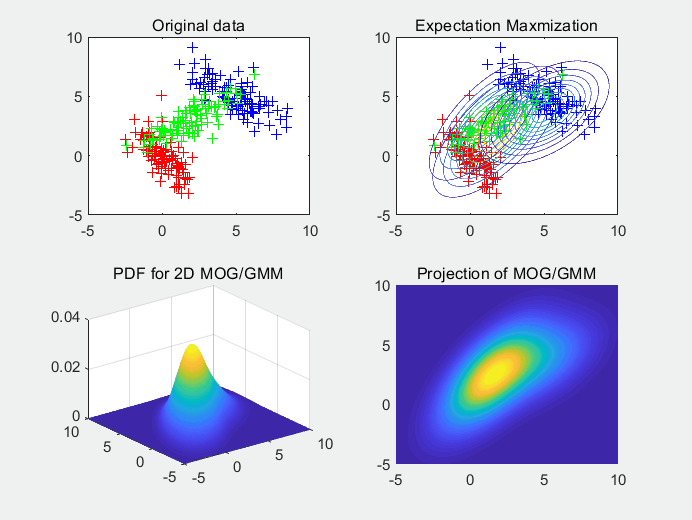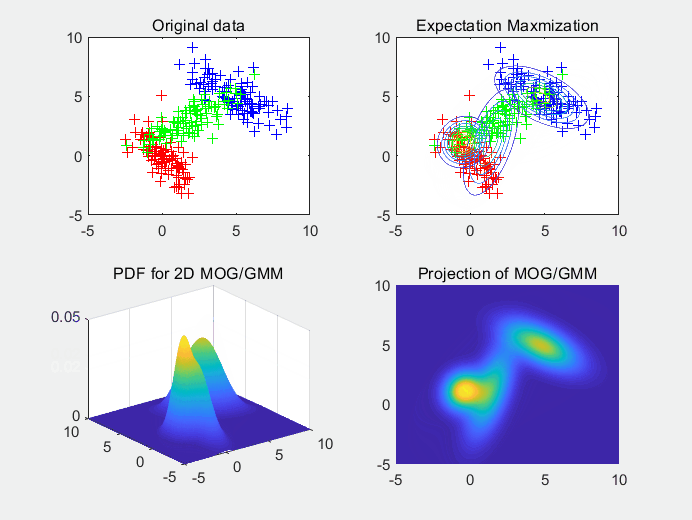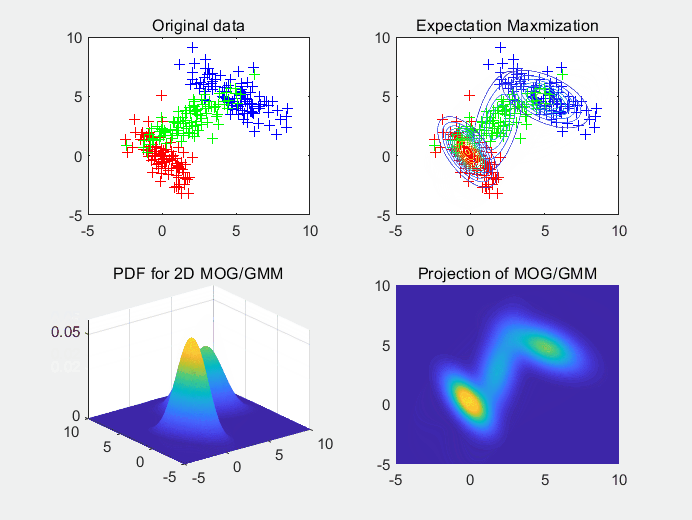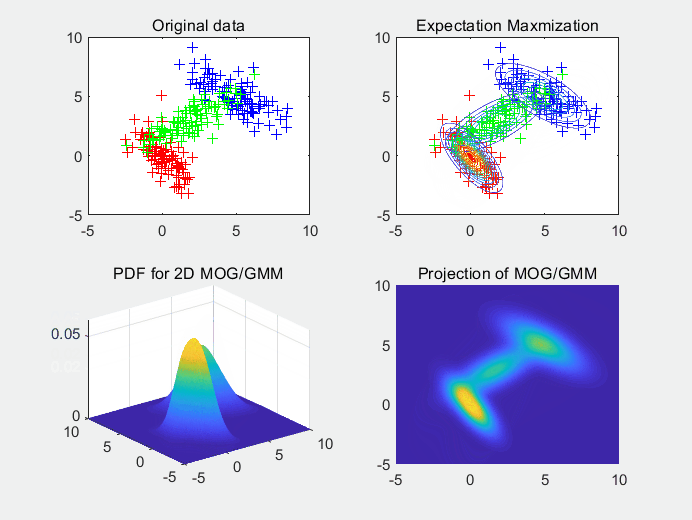

GMM的Matlab动态可视化代码

% Author : Weichen GU
% Date   : 3/10th/2020
% Description : Achieve dynamic visualization for GMM/MOG
% Reference : Computer Vision Models, Learning and Inference

% Initialization
clc;
clear;
clf;

% Generate two Gaussians
% data 1
mu1 = [0 0];    sigma1 = [1 -0.9; -0.9 2];
r1 = mvnrnd(mu1,sigma1, 100);
% data 2
mu2 = [5 5];    sigma2 = [3 -2; -2 2];
r2 = mvnrnd(mu2,sigma2, 100);
% data 3
%mu2 = [2 3];    sigma2 = [3 2; 2 2];
%r3 = mvnrnd(mu2,sigma2, 100);
% Plot these Gaussians 
figure(1)
for i = 1:2
    subplot(2,2,i);
    title('Original data');
    plot(r1(:,1),r1(:,2),'r+');
    hold on;
    plot(r2(:,1),r2(:,2),'b+');
    %plot(r3(:,1),r3(:,2),'g+');
    title('Original data');
    %axis([-10 15 -10 15])
    hold off;
end
data = [r1; r2]; % Our dataset
%data = [r1; r2; r3]; % Our dataset

% Do gmm fitting process
fit_gmm(data,2,0.1);

%% Using Gaussian Mixture Model to do clustering
% Input:    data        - data,
%           k           - the number of Gaaussians,
%           threshold   - the precision of the stopping threshold
% Output:   lambda      - the weight for Gaussians
%           mu          - the means for Gaussians
%           sigma       - the covariance matrix for Gaussians
function [lambda, mu, sigma] = fit_gmm(data, k, precision)

    [num,dim] = size(data);   % Get the size and dimension of data
    lambda = repmat(1/k,k,1); % Initialize weight for k-th Gaussian to 1/k
    
    randIdx = randperm(num);   % do randomly permutation process
    mu = data(randIdx(1:k),:); % Initialize k means for Gaaussians randomly 
    
    dataVariance =  cov(data,1);    % Obtain the variance of dataset ∑(x-mu)'*(x-mu)/ num
    sigma = cell (1, k);            % Store covariance matrices
    % sigma is initialized as the covariance of the whole dataset
    for i = 1 : k
        sigma{
     i} = dataVariance;
    end
    % x,y is used to draw pdf of Gaussians
    x=-5:0.05:10;
    y=-5:0.05:10;
    
    iter = 0; precious_L = 100000;
    while iter < 100
        
        % E-step (Expectation)
        gauss = zeros(num, k); % gauss - stores data generated from Gaussian distribution given mu & sigma
        for idx = 1: k
            gauss(:,idx) = lambda(idx)*mvnpdf(data, mu(idx,:), sigma{
     idx});
        end
        respons = zeros(num, k); % respons - stores responsibilities
        
        total = sum(gauss, 2);
        for idx = 1:num
            respons(idx, :) = gauss(idx,:) ./ total(idx);
        end

       % M-step (Maximization)
       responsSumedRow = sum(respons,1);
       responsSumedAll = sum(responsSumedRow,2);
       for i = 1 : k
          % Updata lambda
          lambda(i) =  responsSumedRow(i) / responsSumedAll;
          
          % Updata mu
          newMu = zeros(1, dim);
          for j = 1 : num
              newMu = newMu + respons(j,i) * data(j,:);
          end
          mu(i,:) = newMu ./ responsSumedRow(i);
          
          % Updata sigma
          newSigma = zeros(dim, dim);
          for j = 1 : num
              diff = data(j,:) - mu(i,:);
              diff = respons(j,i) * (diff'* diff);
              newSigma = newSigma + diff;
          end
          sigma{
     i} = newSigma ./ responsSumedRow(i);
       end
       
        subplot(2,2,2)
        title('Expectation Maxmization');
        hold on
        [X,Y]=meshgrid(x,y);

        stepHandles = cell(1,k);
        ZTot = zeros(size(X));

        for idx = 1 : k
           Z = getGauss(mu(idx,:), sigma{
     idx}, X, Y);
           Z = lambda(idx)*Z;
           [~,stepHandles{
     idx}] = contour(X,Y,Z);
           ZTot = ZTot + Z;
        end
        hold off
       
        subplot(2,2,3) % image 3 - PDF for 2D MOG/GMM
        mesh(X,Y,ZTot),title('PDF for 2D MOG/GMM');

        subplot(2,2,4) % image 4 - Projection of MOG/GMM
        surf(X,Y,ZTot),view(2),title('Projection of MOG/GMM')
        shading interp
        %colorbar
        drawnow();
       
       % Compute the log likelihood L
       temp = zeros(num, k);
       for idx = 1 : k
          temp(:,idx) = lambda(idx) *mvnpdf(data, mu(idx, :), sigma{
     idx}); 
       end
       temp = sum(temp,2);
       temp = log(temp);
       L = sum(temp);
       
       iter = iter + 1;
       preciousTemp = abs(L-precious_L)
       if  preciousTemp < precision
           break;
       else
           % delete plot handles in image 2
           for idx = 1 : k
                set(stepHandles{
     idx},'LineColor','none')
           end
           %set(MStepHamdle,'LineColor','none')
       end
       precious_L = L;
       
    end
end 

function [Z] = getGauss(mean, sigma, X, Y)
    dim = length(mean);

    weight = 1/sqrt((2*pi).^dim * det(sigma));
    [~,row] = size(X);
    [~,col] = size(Y);
    Z = zeros(row, col);
    for i = 1 : row
        sampledData = [X(i,:); Y(i,:)]';
        sampleDiff = sampledData - mean;
        inner = -0.5 * (sampleDiff / sigma .* sampleDiff);
        Z(i,:) =  weight * exp(sum(inner,2));
    end

end

总结：

1. 使用EM算法不能保证找到非凸优化问题的全局解。
2. 需要指定GMM高斯函数的数量。

最后给出一个纯净的GMM(没有可视化)的matlab程序供下载：