杭州学军中学信友队邀请赛之第二题《齐心抗疫》

昨天，我讲解了关于上周日比赛的第一题，这次，我来讲一讲关于比赛第二题的解题思路与程序。
首先，

题目

B. 齐心抗疫

---

时间限制：300ms
空间限制：512MB

题目描述

某市有n个县，并有n-1条双向高速公路连通这n个县，每条高速公路的长度为1。

受疫情影响，第i个县里有a[i]个患者。为了让疫情较轻的县帮助疫情严重的县，政府
决定选择两个县x,y，x的疫情较为不严重， y的疫情较为严重（即a[x] <= a[i]），并
让县x帮助县y 。县x将为县y的每一个患者送一份医疗物资，以最短路从x到y运
输，运送一份医疗物资通过长度为1的高速公路需要花费1元，由政府掏钱报销。

请问如果任意选择两个县实施帮扶计划，政府最多要花多少钱？

输入描述

第一行，一个正整数 。
第二行， 个正整数，第 个表示 。
接下来 行，每行两个数 ，表示县 和县 之间有一条高速公路。

输出描述

一个数表示答案。

样例输入

8
3 1 4 1 5 9 2 6
1 2
2 3
2 4
1 5
5 6
4 8
3 7

样例输出

45

嘿，这轮我们先把题目全部拽出来。

限制及约定

子任务编号	$n<=$	分值
1	2	18
2	100	30
3	2000	19
4	50000	33

对于所有数据，$2<=n<=50000$，$1<=a[i]<=1000$。

题目分析

这个题目很容易理解，就是通过各方面条件让政府花更多的钱。。。出题人一定是一个有钱的大佬。
于是，我们按照题目来看，就可以实现一种特别粗糙的算法：直接硬怼！不过经过上一道题，我猜测硬怼是不行的。

硬怼也有硬怼的方法。方法就是暴力枚举。先枚举从每一个点出发，通过递归查找需要花最多钱的路径。此时，算法的时间复杂度应该是$n^3|n^2$。我们算一算，以$n^2$为基础，算一算能拿到多少分。首先$2^2$没问题，能拿到18分。$100^2$也差不多，10000，能拿到30分。$2000^2$似乎有点勉强。$50000^2$不用说了， 拿不到分。我们只能看看在实际上测试机器能拿到多少分。

在提交之前，我们需要解决很多问题。
首先，如何存储可以走的路呢？
我立马想到了点阵图，map[i][j]说明i,j之间有通路。这种方法特点是快，但缺点是需要的空间很大，二维数组2000就差不多爆炸了。

其次，递归中间如何书写？
…
还有很多问题，先让我们写写程序吧。
超级慢版程序：

#include
using namespace std;
int num[50001];
int map[2001][2001];
int mmax=-9999999;
int n;int sum;

int search(int w,int last,int llast)
{
     
	int mmmax=num[w]>num[llast]? w:llast;
	if(mmax<num[mmmax]*sum) mmax=num[mmmax]*sum;
	int flag=0;
	for(int i=1;i<=n;i++)
	{
     
		if(map[w][i]&&i!=last)
		{
     
			flag=1;
			sum++;
			search(i,w,llast);
			sum--;
		}
	}
}

int main()
{
     
	cin>>n;
	for(int i=1;i<=n;i++)
		cin>>num[i];
	for(int i=1;i<n;i++)
	{
     
		int x,y;
		cin>>x>>y;
		map[x][y]=1;
		map[y][x]=1;
	}
	int w;
	for(int i=1;i*i<=n;i++)
	{
     
		sum=0;
		w=search(i,0,i);
	}
	cout<<mmax;
	return 0;
}

来吧，我们来看看得了多少分吧！

很显然，超时得到48分。我就说，暴力肯定不行。

接着分析题目

接着，我思考思考…ei，我们还没有剖解这道题终究需要求什么。

剖析

假设$f(x,y)$表示从x到y的最短路径，列出方程式，我们要求的就是：
$$max(a(x),a(y))\ast f(x,y)$$
可以分解为：
$$max(a(x)\ast f(x,y),a(y)\ast f(x,y))$$
那就很明白了，只要将f(x,y)和x最大化就OK哩；
接下来，我引入一个概念：树的直径
在一棵树里，最远的两个点构成的路径就是树的直径。直径的两个端点上距离任何一个点都要远。
我来证明下吧。

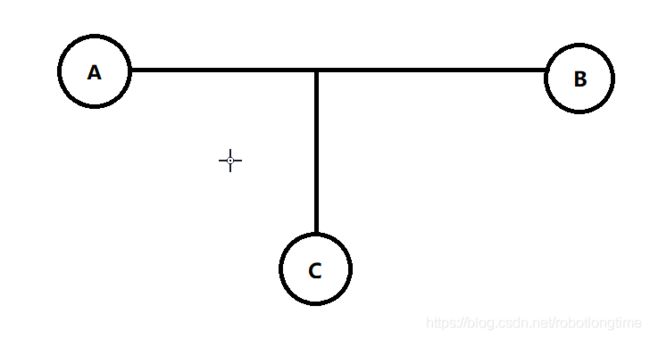
假设点A与点B是在一棵树上的，且他们之间的线段就是树的直径：

在它们之间，有一个瞎参和的 点C。
接着又来一个瞎参和的 的点D。

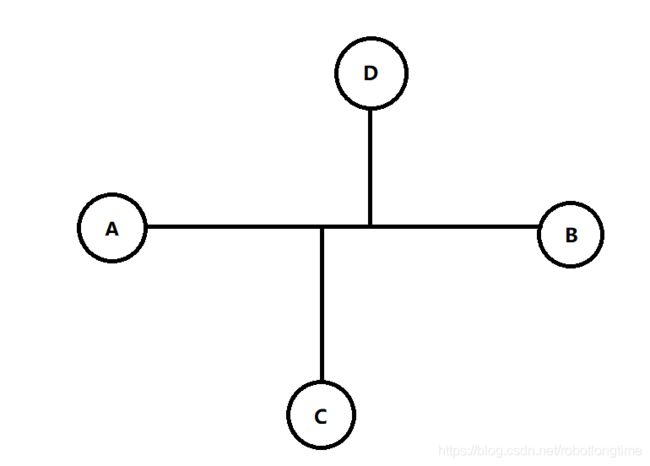
接着问题来了！从点C到点B是最远的还是到点D最远？
到点B？有可能。
到点D？也有可能。来，咱们再来画图：
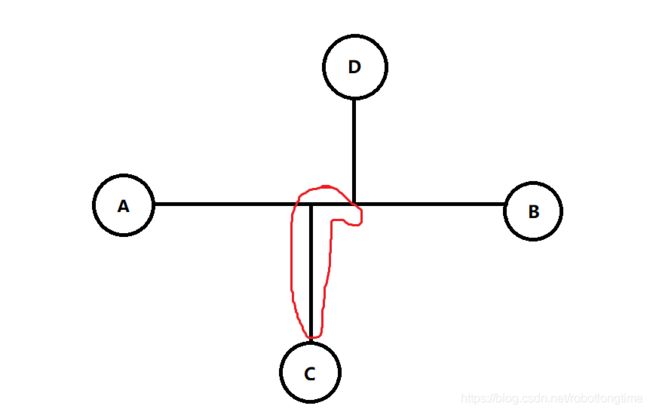用红笔圈出的部分显然相同，剩下的线段比长度可以换成：谁距离A最远。那就肯定是B了，要不然相对于点A到点B是树上的最长路径这条依据。
到此为止，论证结束，无论如何，点A到点C或点B到点C是最长的路径。

程序实现

接下来，就是令人欢喜的程序实现部分了！稍微有点长，谅解。大家慢慢看。

#include
using namespace std;
int a[50001];
int head[200005],nxt[200005],to[200005];
int de[50001],dee[50001],deep[50001];
int tot=0;       //所在点 

void add(int u,int v)     //增加路径 
{
     
    nxt[++tot]=head[u];
    to[tot]=v;
    head[u]=tot;
}

void dfs(int x,int y,int *d)
{
     
    d[x]=d[y]+1;
    for(int i=head[x];i;i=nxt[i])
    {
     
        if(to[i]!=y)
        {
     
            dfs(to[i],x,d);
        }
    }
}

int main()
{
     
    int n,u,v,root2=0,ma=0,root1=0;
    cin>>n;
    for(int i=1;i<=n;i++)
    {
     
        cin>>a[i];
    }
    for(int i=1;i<=n-1;i++)
    {
     
        cin>>u>>v;
        add(u,v);add(v,u);
    }
    dfs(1,0,de);
    for(int i=1;i<=n;i++)
    {
     
        if(de[i]>ma)
        {
     
            ma=de[i];
            root1=i;
        }
    }
    dfs(root1,0,dee);
    ma=0;
    for(int i=1;i<=n;i++)
    {
     
        if(dee[i]>ma)
        {
     
            ma=dee[i];
            root2=i;
        }
    }
    dfs(root2,0,deep);
    int res=0;
    for(int i=1;i<=n;i++)
    {
     
        res=max(res,max(dee[i]-1,deep[i]-1)*a[i]);
    }
    cout<<res;
    return 0;
}

感谢大家支持！

---

今天看见有人关注我了？哦豁，第一个哦！！！