学习之旅-红黑树之插入新节点

关于红黑树的帖子不可谓不多。一开始我看的是july的帖子（链接：http://blog.csdn.net/v_JULY_v/article/details/6105630），但是删除的时候他这系列说的不是很明白。也可以看维基百科上对于红黑树的说明，说的很清楚，但是全是英文的。。。

 这里主要讲讲我自己的理解，以我自己学习红黑树的经历来说的。

红黑树就是查找二叉树的一种，因为一般查找二叉树有可能退化成一条单链表。比如在你插入的节点的key是排好序的的时候有可能就会成为一条链表。所以就有了红黑树。使得不会退化成链表。

说到红黑树，就不得不说他的五大特点，这也是红黑树得以保持平衡的关键。

1. 每个结点要么是红的要么是黑的。  
2. 根结点是黑的。  
3. 每个叶结点（叶结点即指树尾端NIL指针或NULL结点）都是黑的。  
4. 如果一个结点是红的，那么它的两个儿子都是黑的。  
5.  对于任意结点而言，其到叶结点树尾端NIL指针的每条路径都包含相同数目的黑结点。

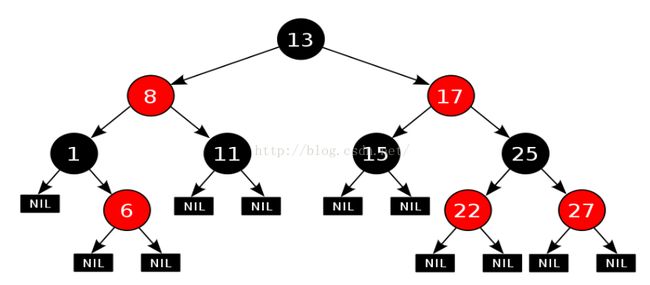
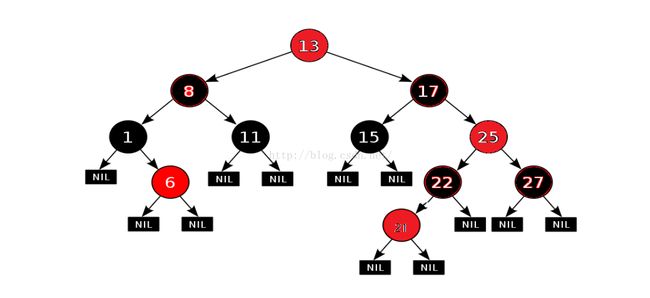
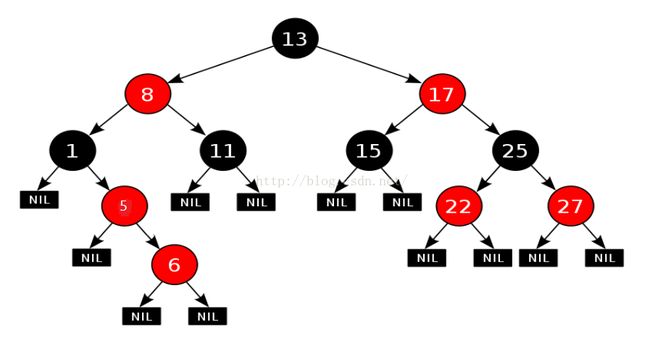
我觉得1,2,3，4都很好理解，主要是5，这个可以看下面这个图。

从图上可以明确看出，从根节点13到每个叶子节点（NIL）的所有路径上都只有3个黑色的黑色节点，比如 13(黑)->8（红）->1（黑）->NILL黑)。

那么现在目标很明确。我要构造这样的一颗二叉树。分为下面的几个步骤：

一、先进行二叉查找树的插入操作。 

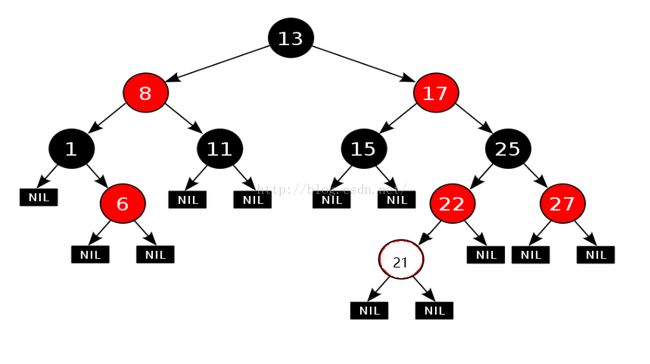
二叉查找树的插入很简单，先把要插入的节点的key与根进行比较，小则和根的左孩子做比较，大则跟右孩子作比较，直到找到叶子节点。值得注意，这样的插入操作，新插入的节点必定是原来叶子节点的位置。比如在上面的树种插入节点21，则会是下面的情况，暂且不考虑节点21的颜色该是红还是黑：

二、新插入的节点可能破坏了红黑树的平衡，所以进行平衡调整。

现在按照二叉查找树的插入方式插入了节点21，那么这个21该是什么颜色呢？

1、黑色，如果是黑色，那么不管原来的红黑树是什么样的，这样一定会破坏平衡，因为原来的树是平衡的，现在在这一条路径上多了一个黑色，必然违反了性质5（不记得的时候多看几遍性质，并理解是最好的）。
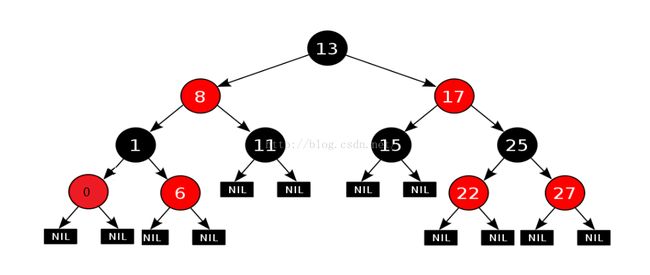
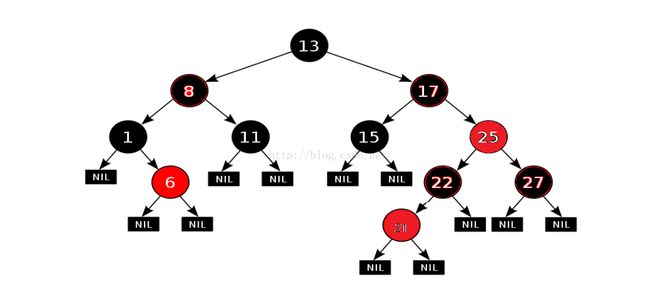
2、红色，如果新插入的点是红色的，那么也有可能会破坏平衡，主要可能是违反了性质4，比如上图中，新插入的点21的父节点22为红色。但是却有一种特殊情况，比如上图中，如果我插入一个key=0的节点。把0这个节点置为红色，并不会影响原来树的平衡，因为0的父节点是黑色。如下图：

好歹也有不需要调整的情况，所以还是选择把新插入的节点颜色置为红色。

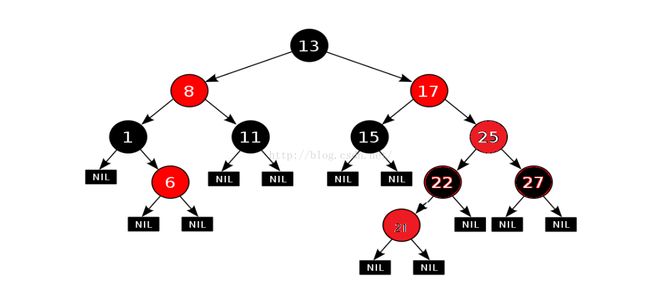
如果新插入的点是红色，那么就会有可能破坏平衡，像上面的新节点21 。这个时候我们把，21的颜色置为红色。则他的父亲也是红色，违反性质4，需要调整，怎么调整呢？现在就要看新插入的点的叔叔节点了。上面的节点27 。

因为21的叔叔27是红色的。所以要保持平衡，可以把25设置成红色，22,27分别设置成黑色，是不是也平衡了呢？如下图：

明显，单看以25为根的子树，是平衡了。但是带来了新的问题。17是红色的。孩子25也是红色的。还是违反了我们的性质4。所以我们还得再看25 。

这个时候还是同样的问题。25的父亲，叔叔都是红色的。重复上面的操作， 得到下面的树。

显然整棵树都平衡了。但是还有有问题。根节点颜色成了红色，这个好办，直接设置根节点颜色为黑色即可。于是整棵树平衡。并且没有违反红黑树的五大性质。如下图：

以上是插入的点的叔叔是红色的。但是如果叔叔是黑色的呢？？

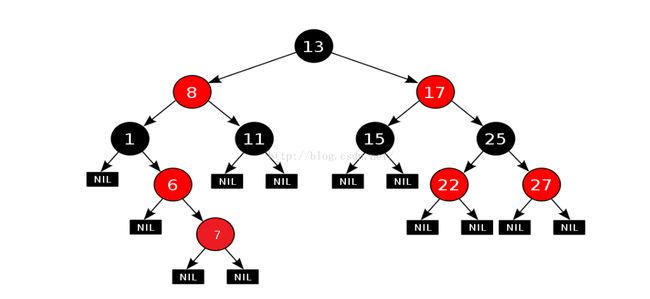
比如我需要在最原始的树上插入一个key=7的点。经过二叉查找树的插入操作之后，如下图

明显插入的节点7已经破坏平衡，并且父亲是红色，叔叔是NIL（黑色），这个时候我们又该怎么办呢？

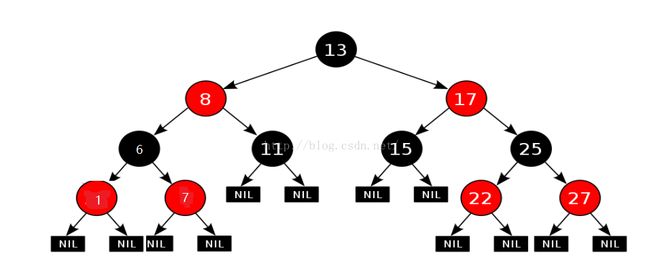
这个时候假设我们能把6放到1的位置，1变成6的左孩子，并且交换1和6的颜色，那么是不是平衡了呢？如下图：

是不是很神奇呢？其实这个操作的名字叫做树的旋转。注意：设置颜色不是旋转的一部分。上面采用的就是树的左旋，以1作为旋转点（需要旋转的子树的根节点）。下面来看一种右旋。

这是插入7的情况，那假如我要插入的是5呢？执行二叉查找树树的操作后是这样的：

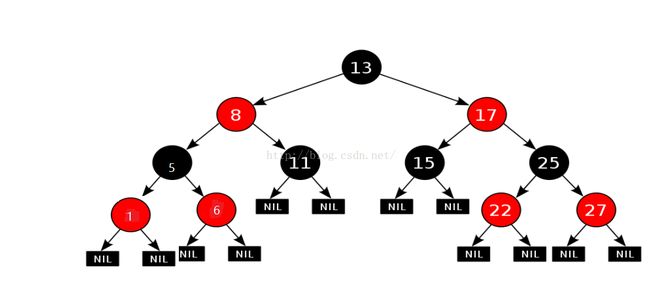
这个时候我们要变通一下，把这张情况转换成上一种情况，也就是插入7的情况，是不是我们就会了。。但是怎么转换呢？还是树的旋转，旋转成下图。

这就是树的右旋，旋转6这颗子树。然后再像上面插入节点7一样，先交换1和5的颜色，左旋子树1 ，最后就平衡了。

执行这个操作的情况，我觉得按我的理解，很形象生动的就是需要自己，父亲，祖父，叔叔连成一个闭合的图形的时候不是三角形，而是菱形。

如下图

最后完整的插入代码如下。跟nginx的红黑树的插入代码差不多。。因为我参照了。。还有一种写法就是像维基百科那样每个情况都用一个函数去写。那样可读性高。。。

/*
** tst_rbtree.h
** create by lj
*/

#ifndef _TST_RBTREE_H_
#define _TST_RBTREE_H_

#if 0
#define tst_rbt_inline inline 
#else
#define tst_rbt_inline
#endif

typedef struct tst_rbtnode_t tst_rbtnode;

/* 树的节点结构 */
struct tst_rbtnode_t
{
	unsigned int	key;
	tst_rbtnode*		lchild;
	tst_rbtnode*		rchild;
	tst_rbtnode*		parent;
	unsigned char	color;
	unsigned char	data;
};


typedef struct tst_rbtree_t tst_rbtree;
typedef void(*tst_rbt_insert_func)(tst_rbtnode* root, tst_rbtnode* node, tst_rbtnode* sen);

/* 树结构 */
struct tst_rbtree_t
{
	tst_rbtnode*	root;
	tst_rbtnode*	sentinel;//哨兵
	tst_rbt_insert_func	insert;
};

/* define */
#define tst_rbt_is_leaf(tree, n)	((tree)->sentinel == (n))
#define tst_rbt_set_red(n)			((n)->color = 1)
#define tst_rbt_set_black(n)		((n)->color = 0)
#define tst_rbt_is_red(n)			((n)->color)
#define tst_rbt_is_black(n)			(!tst_rbt_is_red(n))
#define tst_rbt_copy_color(n1,n2)	((n1)->color = (n2)->color)
#define tst_rbt_parent(n)			((n)->parent)
#define tst_rbt_grandpa(n)			(((n)->parent)->parent)
#define tst_rbt_is_lchild(n)		((n)==(tst_rbt_parent(n)->lchild))
#define tst_rbt_is_rchild(n)		((n)==(tst_rbt_parent(n)->rchild))

#define tst_rbt_sibling(n)			(tst_rbt_parent(n)->lchild==(n)	\
									?tst_rbt_parent(n)->rchild	\
									:tst_rbt_parent(n)->lchild)

#define tst_rbt_lruncle(n,lr)			(tst_rbt_grandpa(n)->lr##child)

#define tst_rbt_uncle(n)			((tst_rbt_parent(n)==(tst_rbt_grandpa(n)->lchild))	\
									?(tst_rbt_grandpa(n)->rchild)				\
									:(tst_rbt_grandpa(n)->lchild))

#define tst_rbt_init(tree, psentinel, i)		\
do											\
{											\
	tst_rbt_set_black(psentinel);				\
	(tree)->root = psentinel;				\
	(tree)->sentinel = psentinel;			\
	(tree)->insert = i;						\
} while (0)

#define tst_rbt_node_init(node, nkey )			\
do											\
{											\
	memset(node, 0x00, sizeof(tst_rbtnode));	\
	(node)->key = nkey;						\
} while (0)

#define tst_rbt_node_reset(node) tst_rbt_node_init(node, 0)

/* 一些操作函数 */
void tst_rbt_insert_default(tst_rbtnode* parent, tst_rbtnode* node, tst_rbtnode* sentinel);
void tst_rbt_insert(tst_rbtree* tree, tst_rbtnode* node);
void tst_rbt_delete(tst_rbtree* tree, tst_rbtnode* node);
void tst_rbt_free(tst_rbtree* tree);

tst_rbtnode* tst_rbt_find(tst_rbtree* tree, tst_rbtnode* sentinel,unsigned int key);

tst_rbt_inline tst_rbtnode* tst_rbt_min_node(tst_rbtnode* node, tst_rbtnode* sentinel);

#endif

源文件：

/*
** tst_rbtree.c
** create by lj
*/

#include 
#include 
#include 
#include "tst_rbtree.h"


static tst_rbt_inline void tst_rbt_rotate_left(tst_rbtnode** root, tst_rbtnode* node, tst_rbtnode* sentinel);
static tst_rbt_inline void tst_rbt_rotate_right(tst_rbtnode** root, tst_rbtnode* node, tst_rbtnode* sentinel);

/*
* 二叉查找树的插入
*/
void tst_rbt_insert_default(tst_rbtnode* parent, tst_rbtnode* node, tst_rbtnode* sentinel)
{
	tst_rbtnode** p;

	for (;;)//为啥有的人喜欢for做死循环呢？因为编译优化之后是一个jmp，而while（true）还需要test或者cmp比较。多指令
	{
		p = (node->key < parent->key) ? &parent->lchild : &parent->rchild;
		if (*p == sentinel)	//找到了叶子节点上了
		{
			break;
		}
		parent = *p;
	}

	//当前结点插在叶子节点的位置
	*p = node;
	node->parent = parent;
	node->lchild = sentinel;
	node->rchild = sentinel;
	//当前结点为红色。运气好的话，父节点颜色是黑色，还不用调整。
	tst_rbt_set_red(node);
}

void tst_rbt_insert(tst_rbtree* tree, tst_rbtnode* node)
{
	assert(tree && node);

	tst_rbtnode *sen, **root;
	root = &tree->root;
	sen = tree->sentinel;

	/* 新插入的点是根节点 */
	if (*root == sen)
	{
		*root = node;
		node->parent = NULL;
		node->lchild = sen;
		node->rchild = sen;
		tst_rbt_set_black(node);

		return;
	}

	//调用上面的tst_rbt_insert_default（）
	tree->insert(*root, node, sen);

	/* 重新平衡红黑树 */
	while (node != *root && tst_rbt_is_red(tst_rbt_parent(node)))
	{
		//node父节点是红色
		if (tst_rbt_parent(node) == tst_rbt_grandpa(node)->lchild)
		{	
			//父节点是祖父的左孩子
			if (tst_rbt_is_red(tst_rbt_lruncle(node, r)))
			{
				//叔叔是红色。调整颜色
				tst_rbt_set_red(tst_rbt_grandpa(node));
				tst_rbt_set_black(tst_rbt_parent(node));
				tst_rbt_set_black(tst_rbt_lruncle(node, r));
				node = tst_rbt_grandpa(node);
				//循环回去再看node的parent的情况
				//假如最后到根节点，这个时候根节点设置成红色。需要后面设置根节点为黑色
			}
			else
			{
				//叔叔是黑色。旋转树
				if (tst_rbt_is_rchild(node))
				{
					//父节点是左孩子，自己是右孩子，这个时候就是自己，父亲，祖父，叔叔连成闭合图形是菱形
					node = tst_rbt_parent(node);
					tst_rbt_rotate_left(root, node, sen);
				}
				tst_rbt_set_red(tst_rbt_grandpa(node));
				tst_rbt_set_black(tst_rbt_parent(node));
				tst_rbt_rotate_right(root, tst_rbt_grandpa(node), sen);
				//旋转之后就ok，循环结束
			}
		}
		else
		{	
			//父节点是祖父的右孩子，与上面是左孩子的操作相反就好。
			if (tst_rbt_is_red(tst_rbt_lruncle(node,l)))
			{	
				//叔叔是红色。调整颜色
				tst_rbt_set_red(tst_rbt_grandpa(node));
				tst_rbt_set_black(tst_rbt_parent(node));
				tst_rbt_set_black(tst_rbt_lruncle(node,l));
				node = tst_rbt_grandpa(node);
			}
			else
			{
				if (tst_rbt_is_lchild(node))
				{
					node = tst_rbt_parent(node);
					tst_rbt_rotate_right(root, node, sen);
				}
				tst_rbt_set_red(tst_rbt_grandpa(node));
				tst_rbt_set_black(tst_rbt_parent(node));
				tst_rbt_rotate_left(root, tst_rbt_grandpa(node), sen);
			}

		}
	}
	tst_rbt_set_black(*root);
	return;
}

/*************************************************************************************
**    如下图：20 这个节点左旋 或者 右旋
**                                                                                   
**           30                  30    		          10                   10        
**           / \                 / \		          / \                  / \       
**          20  31    左旋      22   31		         9   20      左旋     9   22     
**         / \      ------->   / \          或者        / \     ------->     / \      
**       18  22    <-------   20  23                  18   22  <--------   20   23  
**           / \      右旋   / \   			               / \   右旋     / \     	
**         21   23          18  21			              21  23        18   21   	
**         										     					  			   
***************************************************************************************/
static tst_rbt_inline void 
tst_rbt_rotate_left(tst_rbtnode** root, tst_rbtnode* node, tst_rbtnode* sentinel)
{
	tst_rbtnode* temp;

	temp = node->rchild;
	node->rchild = temp->lchild;	//相当于把21变成20的右孩子

	if (temp->lchild != sentinel)
	{
		temp->lchild->parent = node;//21位置改变之后，重新设置他的parent
	}
	if (node == *root)
	{
		*root = temp;				//如果node是根节点。则temp是根节点
	}
	else if (node == tst_rbt_parent(node)->lchild )
	{
		tst_rbt_parent(node)->lchild = temp;//第一图，node在父节点的左孩子节点
	}
	else
	{
		tst_rbt_parent(node)->rchild = temp;//第二图，node在父节点的右孩子节点
	}
	temp->parent = tst_rbt_parent(node);
	temp->lchild = node;
	node->parent = temp;

}

static tst_rbt_inline void 
tst_rbt_rotate_right(tst_rbtnode** root, tst_rbtnode* node, tst_rbtnode* sentinel)
{
	tst_rbtnode* temp;
	temp = node->lchild;
	node->lchild = temp->rchild;

	if (temp->rchild != sentinel)
	{
		temp->rchild->parent = node;
	}

	if (node == *root)
	{
		*root = temp;
	}
	else if (node == tst_rbt_parent(node)->lchild)
	{
		tst_rbt_parent(node)->lchild = temp;
	}
	else
	{
		tst_rbt_parent(node)->rchild = temp;
	}
	temp->parent = tst_rbt_parent(node);
	temp->rchild = node;
	node->parent = temp;
}

以上说明、代码如果有什么问题，请斧正，感激不尽。

谢谢！