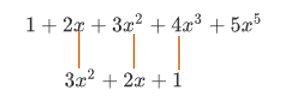快速傅立叶变换算法详解（小白也能看懂的FFT教程）

写在前面

我为什么要写这篇博客？

\quad 如果你随便拉几个OI党，问他们最难理解的几个算法，FFT一定榜上有名。我从开始尝试理解FFT算法到真正理解FFT算法之间间隔了一年之久，但是当我真正理解了这个算法之后，我发现在之前无法理解这个算法，是因为只要我一去搜索FFT，铺天盖地的都是信号处理相关的知识，然而很多信号处理领域的名词（时域、频域之类）事实上和FFT算法本身毫无关系，FFT其实只要简单地从数学层面上去理解就可以。

\quad 我一直都希望有一天把自己理解的FFT过程写成一篇blog，让后来的初学者可以不因为网上形形色色的FFT解释而迷茫。但是由于懒（毕竟要写好多的嘛），我一直没有尝试写这篇blog。由于我碰巧需要讲一下FFT算法，因此在准备完课件之后我决定把这篇早就该写的blog补上，希望更多的人可以更快的学会FFT算法。

正文

\quad FFT其实并不是一个特别难的算法，现在我们就来一起看看它的本质。

卷积

\quad FFT是一个用来加速卷积计算的方法，那我们就先来看看，什么是卷积。

\quad 考虑两个多项式相乘，其中$f(x)=1+2x+3x^2+4x^3+5x^{5}g(x)=1+2x+3x^2$

\quad ps：这里发现了一个小疏漏，我本来想写的是$5x^4$，但是由于图都做好了，就不改了，这里的小笔误不会对后面的过程有任何影响。

\quad 我们的目标是计算$h(x)=f(x)g(x)$每一项的系数

\quad 它们乘积的过程是怎样的呢？

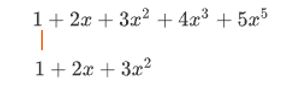
\quad 首先，乘积多项式的常数项应该由两个常数1相乘得到

\quad 然后，我们把连线系数的乘积加和，得到了乘积多项式的一次项

\quad 得到二次项

\quad 得到三次项，后面的同理

\quad 我们发现这个乘积的关系连成线是扭在一起的，所以我们管这种运算叫做卷积

\quad 多项式乘积的形式可以很自然的类比到整数乘法

\quad 比如：

$12345=5+4\ast 10+3\ast 10^2+2\ast 10^3+1\ast 10^4$
$123=3+2\ast 10+1\ast 100$

\quad 我们只需要把x换成10就会很容易发现多项式乘法和整数乘法之间的关系，最后算出来的结果处理一下进位问题，就是最终整数乘法的结果。

\quad 如果我们把第二个多项式倒过来会发生什么？

\quad 两个1相乘，得到常数项

\quad 得到一次项

\quad 得到二次项

\quad 三次项，后面的同理

\quad 我们发现这样的话就是对应位置相乘然后加和，是不是好看了很多？当然，这对我们求解FFT没有任何帮助，但是这可以帮助你理解在实际应用中为什么很多完全不“卷”东西被称作是卷积。 比如说信号平滑和神经网络中的卷积层，其实你只需要把它“扭一下”，它就是卷积了。

如何加速计算卷积？

\quad 朴素计算卷积的时间复杂度是$O(n^2)$的（枚举两个多项式的每一项相乘）

\quad 如果停留在这样的形式，我们几乎不可能找到一个加速卷积计算的方法。

\quad 换一个思路，我们知道，对于一个（n-1）次多项式，我们只需要n个点的取值，就可以列出n个方程从而解出n个系数。

\quad 学过高斯消元的小伙伴这个时候可能会说，解方程是$O(n^3)$的啊，这不是把问题变复杂了吗？这也正是FFT的优雅之处，后面会说明是如何通过奇怪的技巧把反解多项式的时间复杂度降为$O(nlogn)$

\quad 假定$h(x)=f(x)g(x)$是一个n-1次多项式

\quad 如上所述，我们只需要知道多项式n个点的取值就可以反解出多项式的系数

\quad 注意到 $h(a)=f(a)g(a)$

\quad 因此我们可以通过$f(x)$和$g(x)$在n个点的取值来算得$h(x)$在n个点的取值，从而反解出$h(x)$

\quad 那么同样是带入n个点，我们带哪n个点会好算呢？

复平面单位根

\quad 这里我们定义${\omega }_{2n}^i$是$x^{2n}=1$，在复平面上2n个解中的第i个。

\quad 这个公式是很多人噩梦的起点，首先我给大家普及一下，第二个等式成立是因为这个是$e^{i\pi }$的定义，所以看到这个式子不要懵，他就是这样的，无需证明。其次，最后的cos+sin看起来很复杂，这样也不好理解它为什么是$x^{2n}=1$的解，但是其实我们换一个形式就可以看的很清楚。

\quad [hints] 这个图里面数按照我之前所说的表示方法实际上应该写为${\omega }_8^i$，这里是简写的写法

\quad 这是复平面上的单位圆，学过高中复数知识的同学应该多少都听说过，复平面就类似于一个二维坐标轴，坐标(m,n)就代表m+ni这个复数。在复平面上做乘法的规律是，两个复数的模长相乘，极角相加。由于是单位圆，所以圆上每个复数的模长都是1，所谓极角就是复平面上一点与圆心的连线逆时针转到x轴正半轴需要转的度数。就比如说上图中的${\omega }_1$的极角就是45度,也就是$\pi /4$，${\omega }_7$的极角度数是315度，也就是$7\pi /4$

\quad 如果把上面sin，cos的表达式放到复平面上来看，那么2n个解就是把单位圆划分成2n份，每一个点都是一个解。这样的话${\omega }_{2n}^i$的极角度数就为$\frac{2\pi i}{2n}$，它的2n次方的极角度数为$2\pi$的整数倍，且模长不管怎么乘都是1，所以最后也就是1，这也就说明了为什么它是$x^{2n}=1$的解。

\quad 按照上面的图我们可以很容易证明单位根的几个性质：

\quad 1.${\omega }_{2n}^{2i}={\omega }_n^i$ ，（把圆分成2n份取其中的第2i份等于把圆分成n份取第i份）

\quad 2.${\omega }_{2n}^i=-{\omega }_{2n}^{n+i}$ (画在图上很显然)

\quad 3.${\omega }_{2n}^{2n-i}是{\omega }_{2n}^i$的共轭复数（也很显然）

\quad 4.${\omega }_n^{n+i}={\omega }_n^i$ （相当于转了一整圈转了回来）

\quad 不要忘了我们的目的，我们是要带入数进行求值，所以下面我们就试试看把单位根带进去可以发现什么样有趣的性质。

离散傅立叶变换（DFT）

\quad 所谓离散傅立叶变换就是针对n-1次多项式，把$x^n=1$的n个单位根带入求值的过程。

\quad 所谓快速傅立叶变换，就是加速这个求值过程的算法，下面我们看FFT算法是如何加速这个求值过程的。

\quad 为了方便分析，我们考虑（2n-1）次多项式的求值过程。

\quad 我们有多项式$f(x)=a_0+a_{1}x+a_2{x}^2+a_3{x}^3+a_4{x}^4+\dots a_{2n-1}{x}^{2n-1}$

\quad 我们目的是求$f({\omega }_{2n}^0)f({\omega }_{2n}^1)f({\omega }_{2n}^2)f({\omega }_{2n}^3)\dots f({\omega }_{2n}^{2n-1})$

\quad 时刻想着上面的目的有助于不在后面的分析中乱掉。

\quad 我们单拿出f中的偶数项：$f_{even}(x)=a_0+a_2{x}^2+a_4{x}^4+\dots a_{2n-2}{x}^{2n-2}$

\quad 我们发现每一项的参数都是$x^2$的倍数，因此我们不妨把$x^2$看成一个整体

\quad 令$f_0(x)=a_0+a_{2}x+a_4{x}^2+\dots a_{2n-2}{x}^{n-1}$

\quad 因此 $f_{even}({\omega }_{2n}^i)=f_0(w_{2n}^{2i})=f_0({\omega }_n^i)i=1,2,3,\dots ,2n-1$

\quad 又因为${\omega }_n^{n+i}={\omega }_n^i$，所以我们只需要计算$f_0(x)$ 在 ${\omega }_n^0,{\omega }_n^1,\dots ,{\omega }_n^{n-1}$下的值即可

\quad 我们再拿出奇数项：

\quad $f_{odd}(x)=a_{1}x+a_3{x}^3+\dots a_{2n-1}{x}^{2n-1}=x(a_1+a_3{x}^2+\dots +a_{2n-1}{x}^{2n-2})$

\quad 类似地，我们令$f_1(x)=a_1+a_{3}x+a_5{x}^2+\dots +a_{2n-1}{x}^{n-1}$

\quad 我们就可以得出 $f_{odd}({\omega }_{2n}^i)={\omega }_{2n}^i\ast f_1({\omega }_n^i)i=1,2,3,\dots ,2n-1$

\quad 综上我们有$f({\omega }_{2n}^i)=f_{even}({\omega }_{2n}^i)+f_{odd}({\omega }_{2n}^i)=f_0({\omega }_n^i)+{\omega }_{2n}^i{f}_1({\omega }_n^i)$

\quad 我们观察一下，$f_0$和$f_1$是两个n-1次多项式，我们需要求得它们在 ${\omega }_n^0,{\omega }_n^1,\dots ,{\omega }_n^{n-1}$下的值，这不就是上面问题除以二的版本吗！因此我们考虑分治解决这个问题。

\quad 这张图是我用PPT拼凑了好久凑出来的，每次分治，把偶数项和奇数项分开，在一个规模除2的子问题上递归解决问题，递归的边界是只有一个元素的时候，这个时候你甚至不需要带入，结果就是$a_i$，除了最后一层每个框框内的数字是要带入的值，整个框框代表最终求得的值，要代入的表达式都写在了框框旁边。

\quad 请一定要对着上面的分析认真看动上面的图，如果你能自己画出这个图，那么恭喜你，你学会了FFT。

逆离散傅立叶变换（IDFT）

\quad 我们分别求出了$f({\omega }_n^i)$,$g({\omega }_n^i)$

\quad 对应的值相乘，我们得到了$h({\omega }_n^i)$

\quad 那么我们如何快速的反解出$h(x)$呢？

\quad 我们重新看一下带入求值的过程，实际上这个过程可以写成下面形式的矩阵乘法

\quad 我们简记成$W\ast A=F$ （1）

\quad 现在我们有$F$想要反求$A$，怎么办呢？

\quad 考虑一下$W$的共轭矩阵$\overline{W}$（就是对矩阵中的每个元素求共轭）

\quad $W$和$\overline{W}$ 满足如下的性质：

\quad 大家可以自己试着算一下，很好算的。

\quad 于是我们在（1）式左右同时左乘$\overline{W}$可以得到 $nA=\overline{W}F$

\quad 所以只要我们计算出$\overline{W}F$ 就可以算出A的值

\quad 那么$\overline{W}\ast F$是什么呢？

\quad 我们考虑$W\ast F$是把${\omega }_n^i$带到以$a_i$为系数的多项式中求值

\quad $\overline{W}\ast F$是把$\overline{w_n^i}$带入以$f({\omega }_n^i)$为系数的多项式求值！

\quad 也就是说，令$m(x)=f({\omega }_n^0)+f({\omega }_n^1)x+f({\omega }_n^2)x^2+\dots +f({\omega }_n^{n-1})x^{n-1}$

\quad $m(\overline{w_n^i})=n\ast a_i$

\quad 把共轭复数带入求值与原来的方法是完全同理的，再运行一次FFT算法，只不过这次带入共轭复数，我们就可以得到目标多项式的系数值！大功告捷！

\quad 每每讲到这里我都不禁感慨FFT之美。

代码

这里给出我的FFT模板，代码是几年前写的，但是感觉还可以，计算的东西是两个大整数相乘，但是有一点用到的知识没有说，就是这个代码是非递归的写法，也就是预先把元素排好，然后一层一层的向上推

像这样，用到的方法好像叫做蝴蝶变换，我已经记不太清怎么证明了，这里也不细说了，想要了解的同学可以去找一下。

板子是解决两个大整数相乘的问题

#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
struct cpx
{
     
    double a,b;
    cpx(double _=0.0,double __=0.0):a(_),b(__){
     }
    cpx operator +(cpx x) {
     return cpx(a+x.a,b+x.b);}
    cpx operator -(cpx x) {
     return cpx(a-x.a,b-x.b);}
    cpx operator *(cpx x) {
     return cpx(a*x.a-b*x.b,a*x.b+b*x.a);}
}a[4000000],b[4000000],c[4000000];
const double DFT=2.0;
const double IDFT=-2.0;
double trans_form;
const double pi=acos(-1);
int len;
int pos[4000000];
void init()
{
     
    for(int i=0;i<len;i++)
    {
     
        pos[i]=pos[i>>1]>>1;
        if(i&1) pos[i]|=(len>>1);
    }
}
void trans(cpx x[])
{
     
    for(int i=0;i<len;i++) if(i<pos[i]) swap(x[i],x[pos[i]]);
    for(int i=2;i<=len;i<<=1)
    {
     
        int step=i>>1;
        cpx wm(cos(2*pi/(double)i),sin(trans_form*pi/(double)i));
        for(int j=0;j<len;j+=i)
        {
     
            int limit=j+step;
            cpx ww(1,0);
            for(int k=j;k<limit;k++)
            {
     
                cpx a=x[k];
                cpx b=x[k+step]*ww;
                ww=ww*wm;
                x[k]=a+b;
                x[k+step]=a-b;
            }
        }
    }
    if(trans_form==IDFT) for(int i=0;i<len;i++) x[i].a/=(double)len;
}
char s[4000000];
int ans[4000000];
int main()
{
     
    int n=0;
    scanf("%s",s);
    n=strlen(s);
    for(int i=0;i<n;i++) a[i].a=s[n-i-1]-'0';
    scanf("%s",s);
    int ss=strlen(s);
    n=max(n,ss);
    for(int i=0;i<ss;i++) b[i].a=s[ss-i-1]-'0';
    len=1;
    while(len<(n<<1)) len<<=1;
    init();
    trans_form=DFT;
    trans(a);
    trans(b);
    for(int i=0;i<len;i++) c[i]=a[i]*b[i];
    trans_form=IDFT;
    trans(c);
    for(int i=0;i<len;i++) ans[i] = int (c[i].a + 0.5);
    for(int i=0;i<len;i++)
        if(ans[i]>=10)
        {
     
            ans[i+1]+=ans[i]/10;
            ans[i]%=10;
        }
    int top=len-1;
    while(top && !ans[top]) top--;
    if(!ans[top])
    {
     
        cout<<0<<endl;
        return 0;
    }
    while(top>=0)
        printf("%d",ans[top--]);
    return 0;
}

The End