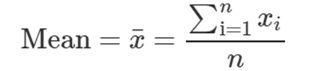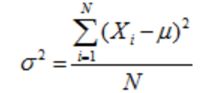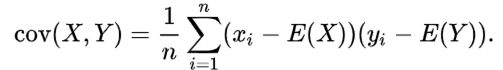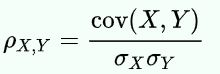统计知识不容忽视：数据科学家必须了解的统计学

全文共2415字，预计学习时长7分钟

图源：unsplash

 

数据科学初学者们常常会忽视最基础的统计学知识，这是必须重视的大问题。这些统计学概念有助于我们更好地理解不同模块和各种技术，它们是数据科学、机器学习和人工智能领域很多概念的基础。

 

1.集中趋势度量

 

集中趋势的一个度量是找到一组数据中间位置的数值，用它来描述这一组数值。常用的三种度量数值是：

 

· 均值是数据总值的平均数。

 

N个数据总值的均数

· 中位数是有序数据的中间值。中间数优于均值，因为它不受离群数据的影响。

· 众数是数据中出现频率最高的值。

 

2.离散趋势度量

 

离散趋势度量表现的是一组变量（数据项）的相似程度或多样程度。度量方式包括极差、四分位数、四分位数间距、方差和标准差。

· 极差是一组数据中最大值与最小值之差。

 

· 四分位数 是指将指定数据集等分四份后，处于分割点的数值。下四分位数（Q1）处于下25%数值与上75%数值之间，又称“第一四分位数”；第二四分位数是数据集的中间值，又称“中位数”；上四分位数（Q3）处于下75%数值与上25%数值之间，又称“第三四分位数”。

 

四分位数分布

四分位数间距（IQR）是第三四分位数（Q3）与第一四分位数（Q1）的差值，当数据按从小到大排列时，四分位数间距是中间50%值的间距。在度量离散时，四分位距优于极差，因为它不受离群数据的影响。

 

· 所有数据点（总体均值为μ）的方差，每个数据点都用Xi表示，除以数据个数N。

 

方差的数学方程式

· 标准差：是方差的算术平方根，总体的标准差用σ表示。在扩散程度小的数据集中，所有值都非常靠近均值，于是方差和标准差就会很小。如果一组数据很分散，距均值都很远，方差和标准差就会很大。

 

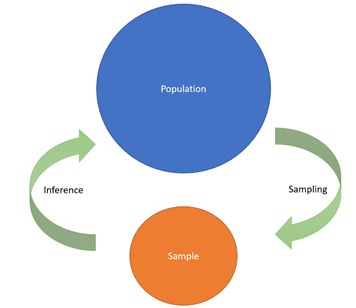
3.总体与样本

 

总体是指全部可用数据值。数据集的一个样本是总体的一部分，或是它的子集。样本数量一定比取样的总体小。举个例子：一个国家的所有人作为“总体”，它的子集是一个“样本”，样本总是小于总体。

 

总体与样本的简介图

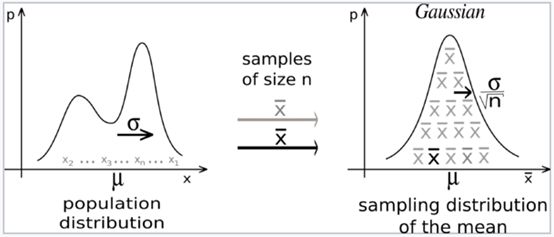
4.中心极限定理

 

中心极限定理是概率论的关键概念，因为它指出正态分布适用于其他分布问题的概率和统计方法。中心极限定理指：当从总体中抽取的样本量足够大时，那么样本均值就会呈现正态分布。无论总体如何分布，该定理都为真。

 

无论总体如何分布，样本分布皆为正态。| 图源：维基百科

中心极限定理的其他关键点：

 

· 样本均值收敛于概率，并且几乎肯定收敛于总体均值的期望值。

· 总体的方差等于样本方差结果和每个样本中的个数。

 

5.抽样和抽样方法

 

抽样是一种统计分析方法，用来选取、操作以及分析数据点的代表子集，从而得出观察数据总体的分布规律和趋势。从数据中取样有很多不同的方法，比较理想的是依靠数据集并根据当前问题选择方法。下面是常用的抽样方法：

 

· 简单随机抽样：使用这个方法时，样本中的每个值都是随机抽取，且总体中每个值被抽取的概率完全一致。

· 分层抽样：使用这种方法时，首先按照特性将总体分成子组（或层级）。适用于：期望使用不同方法量度各个子组，并想要保证各个子组具有代表性。

· 整群抽样：整群抽样中，总体的子组用作抽样单位而非个别值。总体被分成各个子组，又称“整群”，都是随机抽取且都是被调查对象。

· 等距抽样：从抽样框中以等距的方式抽取个别值。选择的间距要保证能提取足够多样本。如果从总量为x的总体中抽取n个值作为样本，应抽取每x/n个作为样本。

 

6.选择性偏差

 

选择性偏差（又称抽样选择偏差）是在总体中非随机抽样导致的系统性错误，总体中一些值被研究的可能性小于其他值，样本从而存在偏差，也就是样本中所有值并非完全平衡或客观。这意味着未完成真正的随机，因此抽取的样本并不是本想分析的总体代表。

 

通常情况下，仅靠对现有数据进行统计分析不能消除选择性偏差，通过相关分析可对选择性偏差的程度进行评估。

 

7.相关

 

相关是衡量变量（或feature或样本或任意组）彼此关联程度的指标。数据科学家几乎每次做数据分析时，都会比较两个变量并找出它们如何相互关联。下面是最常用的相关分析方法。

 

· 协方差

 

两个变量，一个X，一个是Y，E(X)，E(Y)分别是X、Y的均值，“n”则是数据点的总个数。那么X、Y的协方差就是：

 

X和Y协方差的数学计算公式

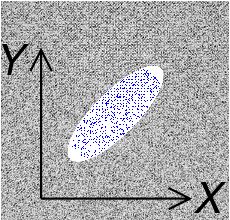
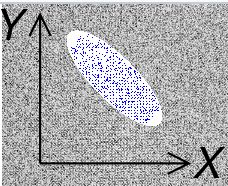
协方差标志代表的是变量间的线性关系。

X、Y的协方差分别为正、负时的样图 | 图源：Wikipedia

· 皮尔逊相关系数

 

皮尔逊相关系数也可以度量两个变量的线性相关。对于两个样本X和Y，σX，σY是它们各自的标准差。那么X、Y的皮尔逊相关系数是：

 

X、Y皮尔逊相关系数的数学方程

它的值在-1和+1之间。

 

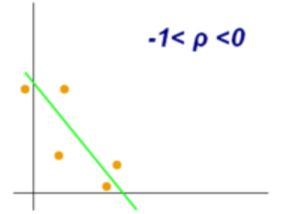
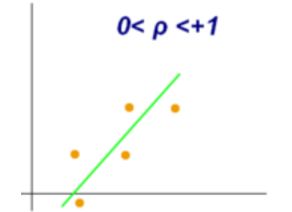
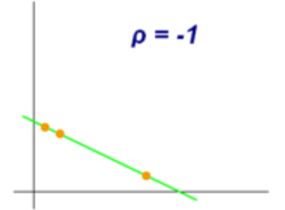
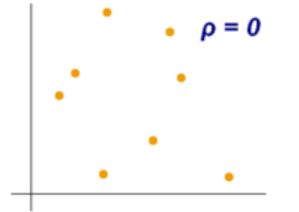
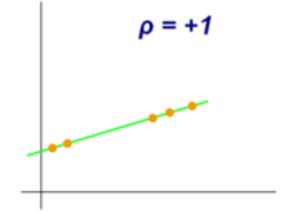
变量的皮尔逊相关系数分别在-1和0，0和+1之间的样图

 

变量的皮尔逊相关系数分别为-1、0和+1时的样图

· 斯皮尔曼等级相关系数

 

斯皮尔曼等级相关系数(SRCC)用单调函数（线性或非线性）来衡量两个样本的依赖性，而皮尔逊相关系数只能衡量线性关系。两个样本之间的斯皮尔曼等级相关系数等于其等级变量之间的皮尔逊相关系数。等级是变量中观测值的相对位置标签。

显然，如果观察的两个变量等级相近，那样本的斯皮尔曼等级相关系数就会比较高；如果两个变量的等级不相近，那样本的斯皮尔曼等级相关系数则会比较低。斯皮尔曼等级相关系数大小在+1和-1之间：

 

· 1代表完全正相关

· 0代表不相关

· −1代表完全负相关

 

文中介绍的统计学中重要知识，初学者们一定要在夯实基础阶段就掌握好。

一起分享AI学习与发展的干货

欢迎关注全平台AI垂类自媒体 “读芯术”

（添加小编微信：dxsxbb，加入读者圈，一起讨论最新鲜的人工智能科技哦～）