如何理解RNN以及LSTM? 深度学习面试_01

鸣谢&参考：

1. ChristopherOlah的博⽂《理解LSTM⽹络》
2. @Not_GOD翻译ChristopherOlah的博⽂《理解LSTM⽹络》
3. 通过⼀张张动图形象的理解LSTM
4. 如何理解LSTM⽹络（超经典的ChristopherOlah的博⽂之July注解版）
5. LSTM相关的典型⾯试题_七月在线
6. @知乎何之源_完全图解RNN、RNN变体、Seq2Seq、Attention机制
7. 七月在线面试题库

1. RNN是怎么从单层网络⼀一步⼀一步构造的？

1.1从单层网络谈起

在学习RNN之前，⾸先要了解⼀下最基本的单层⽹络，它的结构如图：

输⼊是x，经过变换Wx+b和激活函数f得到输出y。

1.2 经典的RNN结构

在实际应⽤中，我们还会遇到很多序列形的数据：

如：
1.⾃然语⾔处理问题。x1可以看做是第⼀个单词，x2可以看做是第⼆个单词，依次类推。
2.语⾳处理。此时，x1、x2、x3……是每帧的声⾳信号。
3.时间序列问题。例如每天的股票价格等等。

为了建模序列问题，RNN引⼊了隐状态h（hidden state）的概念，h可以对序列形的数据提取特征，接着再转换为输出。先从h1的计算开始看：

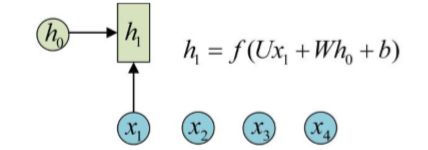
图⽰中记号的含义是：
a）圆圈或⽅块表⽰的是向量。
b）⼀个箭头就表⽰对该向量做⼀次变换。如上图中h0和x1分别有⼀个箭头连接，就表⽰对h0和x1各 做了⼀次变换。

在很多论⽂中也会出现类似的记号，初学的时候很容易搞乱，但只要把握住以上两点，就可以⽐ 较轻松地理解图⽰背后的含义。h2的计算和h1类似。要注意的是，在计算时，每⼀步使⽤的参数U、 W、b都是⼀样的，也就是说每个步骤的参数都是共享的，这是RNN的重要特点，⼀定要牢记。

依次计算剩下来的（使⽤相同的参数U、W、b）

我们这⾥为了⽅便起见，只画出序列长度为4的情况，实际上，这个计算过程可以⽆限地持续下 去。
我们⽬前的RNN还没有输出，得到输出值的⽅法就是直接通过h进⾏计算：

正如之前所说，⼀个箭头就表⽰对对应的向量做⼀次类似于f(Wx+b)的变换，这⾥的这个箭头就表 ⽰对h1进⾏⼀次变换，得到输出y1。
剩下的输出类似进⾏（使⽤和y1同样的参数V和c）：

OK！⼤功告成！这就是最经典的RNN结构，我们像搭积⽊⼀样把它搭好了。它的输⼊是x1, x2, …xn，输出为y1, y2, …yn，也就是说，输⼊和输出序列必须要是等长的。

由于这个限制的存 在，经典RNN的适⽤范围⽐较⼩，但也有⼀些问题适合⽤经典的RNN结构建模，如：
1.计算视频中每⼀帧的分类标签。因为要对每⼀帧进⾏计算，因此输⼊和输出序列等长。
2.输⼊为字符，输出为下⼀个字符的概率。这就是著名的Char RNN

1.3 N --> 1

有的时候，我们要处理的问题输⼊是⼀个序列，输出是⼀个单独的值⽽不是序列，应该怎样建模 呢？实际上，我们只在最后⼀个h上进⾏输出变换就可以了：

这种结构通常⽤来处理序列分类问题。如输⼊⼀段⽂字判别它所属的类别，输⼊⼀个句⼦判断其 情感倾向，输⼊⼀段视频并判断它的类别等等。

1.4 1 --> N

这种1 --> N的结构可以处理的问题有：
1.从图像⽣成⽂字（image caption），此时输⼊的X就是图像的特征，⽽输出的y序列就是⼀段句⼦.
2.从类别⽣成语⾳或⾳乐等 .

1.4 N --> M

下⾯我们来介绍RNN最重要的⼀个变种：N vs M。这种结构又叫Encoder-Decoder模型，也可以称 之为Seq2Seq模型。
原始的N vs N RNN要求序列等长，然⽽我们遇到的⼤部分问题序列都是不等长的，如机器翻译 中，源语⾔和⽬标语⾔的句⼦往往并没有相同的长度。为此，Encoder-Decoder结构先将输⼊数据编码 成⼀个上下⽂向量c：

得到c有多种⽅式，最简单的⽅法就是把Encoder的最后⼀个隐状态赋值给c，还可以对最后的隐状 态做⼀个变换得到c，也可以对所有的隐状态做变换。
拿到c之后，就⽤另⼀个RNN⽹络对其进⾏解 码，这部分RNN⽹络被称为Decoder。具体做法就是将c当做之前的初始状态h0输⼊到Decoder中：

还有⼀种做法是将c当做每⼀步的输⼊：

由于这种Encoder-Decoder结构不限制输⼊和输出的序列长度，因此应⽤的范围⾮常⼴泛，⽐如：
机器翻译：Encoder-Decoder的最经典应⽤，事实上这⼀结构就是在机器翻译领域最先提出的。
⽂本摘要：输⼊是⼀段⽂本序列，输出是这段⽂本序列的摘要序列。
阅读理解：将输⼊的⽂章和 问题分别编码，再对其进⾏解码得到问题的答案。
语⾳识别：输⼊是语⾳信号序列，输出是⽂字序列

2. 如何从RNN起步，一步一步通俗理理解LSTM

2.1 RNN的局限

长期依赖（Long-Term Dependencies）问题 也就是 当明相关信息和当前预测位置之间的间隔不断增⼤时，RNN会丧失学习到连接如此远的信息的能⼒。
换句话说，RNN会受到短时记忆的影响。如果⼀条序列⾜够长，那它们将很难将信息从较早的时 间步传送到后⾯的时间步。

因此，如果你正在尝试处理⼀段⽂本进⾏预测，RNN可能从⼀开始就会遗漏重要信息。在反向传 播期间（反向传播是⼀个很重要的核⼼议题，本质是通过不断缩⼩误差去更新权值，从⽽不断去修正 拟合的函数），RNN会⾯临梯度消失的问题。
因为梯度是⽤于更新神经⽹络的权重值（新的权值=旧权值-学习率*梯度），梯度会随着时间的推 移不断下降减少，⽽当梯度值变得⾮常⼩时，就不会继续学习。

换⾔之，在递归神经⽹络中，获得⼩梯度更新的层会停⽌学习——那些通常是较早的层。由于这些 层不学习，RNN可以忘记它在较长序列中看到的内容，因此具有短时记忆。
然而，幸运的是，有个RNN的变体——LSTM，可以在⼀定程度上解决梯度消失 和梯度爆炸这两个问题！

2.2 LSTM网络

首先，我们介绍两个激活函数：
Sigmoid激活函数与 tanh 函数，Sigmoid是把值压缩到0~ 1之间 ，tanh 是把值压缩到-1 ~1之间 .

Sigmoid激活函数有助于更新或忘记信息，具体表现为：
（1）因为任何数乘以0都得0，这部分信息就会剔除掉； （2）同样的，任何数乘以1都得到它本⾝，这部分信息就会完美地保存下来。

2.2.1 理解LSTM的三个门

1. 忘记门
   
2. 输⼊门
   
   $C_{t-1}$ 更新为 $C_t$
   
3. 输出门

4. 记住公式：

$i_t$: input gate

$f_t$: forget gate

$o_t$: output gate

${\tilde{c}}_t$: new memory cell

$c_t$: final memory cell

$h_t$: hidden state

2.2.2 LSTM变种

GRU: Gated Recurrent Unit

$z_t$是update gate，表示下一个hidden state中有多少信息来自新的hidden state，多少保留原来的旧的hidden state。
如果 z_t 比较接近1的话，$\partial h_t/\partial$$h_{t-1}$就会比较接近1，这样就能确保gradient不会变得太小。
$r_t$是reset gate，用来确定在生成新的candidate hidden state的时候考虑多少上一个hidden state。