机器学习——传统聚类、LDA、深度学习聚类方法
文章目录
-
- 一、基于文本特征的方法
-
-
- 1.K-Means算法
- 2.均值漂移算法
- 3.层次聚类
- 4.谱聚类算法
- 5.DBSCAN密度聚类算法
- sklearn代码
-
- 二、潜在语义分析
- 三、深度学习聚类
聚类的应用场景没有分类广泛,而由于无监督其算法效果也不足已运用到生产环境中去,不过其仍然是机器学习中的一个重要组成部分。文本聚类常见的应用场景就是文档标签生成,热点新闻发现等等,另外,在处理文本特征时,也可以使用聚类形成特征的低维表示。
本文主要从 基于特征、 潜在语义分析、 深度学习两个类型的方法来描述文本聚类这个任务。
一、基于文本特征的方法
特征表示
文本在分类和聚类的任务中,其特征表示都是一样的。参考原创 自然语言处理-文本分类入门
1.K-Means算法
K-means算法是聚类算法中的最常用的一种,其计算简单,运算速度快。但是要求:
- 数据之间的相似度可以使用欧氏距离度量(欧式距离越近的两个数据其相似性越高)
- 提前指定类簇个数
其算法概括为:
1. 初始化k个对象作为初始聚类中心
2. 把各个对象分配给距离它最新的聚类中心点
3. 重新计算聚类中心
终止条件: 没有对象被重新分配 或者 没有聚类中心变化 或者误差平方和局部最小
K-means算法存在问题
- K需要人工确定
- 初始聚类中心点怎么确认。
- 离群点影响显著
对于问题1
可以对数据进行简单分析得到,也可以利用基于结构的算法(如使用平均轮廓系数,越趋近1聚类效果越好)或者基于变化的算法(即定义一个函数,随着K的改变,认为在正确的K时会产生极值)。具体方法可以参见总结
对于问题2
初始聚类中心点可以通过多次随机选择来获取,也可以选择距离尽量大的k个点,或者先采用层次聚类选择K个聚类点并利用这些中心作为初始点
2.均值漂移算法
均值漂移算法经常被应用在图像识别中的目标跟踪、数据聚类等场景。该算法不用指定类别数目,而是通过带宽决定(带宽可以用指定算法估计)。
该算法,对于给定的一定数量样本,首先随便选择一个中心点,然后计算该中心点一定范围之内所有点到中心点的距离向量的平均值,计算该平均值得到一个偏移均值,然后将中心点移动到偏移均值位置,通过这种不断重复的移动,可以使中心点逐步逼近到最佳位置。
1 在数据点中随机选择一个点作为初始中心点。
2 找出离该中心点距离在带宽之内的所有点,记做集合M,认为这些点属于簇C.
3 计算从中心点开始到集合M中每个元素的向量,将这些向量相加,得到偏移向量。
4 将该中心点沿着偏移的方向移动,移动距离就是该偏移向量的模。
5 重复上述步骤2,3,4,直到偏移向量的大小满足设定的阈值要求,记住此时的中心点。
终止条件: 所有的点都被归类
7 分类:根据每个类,对每个点的访问频率,取访问频率最大的那个类,作为当前点集的所属类。
均值漂移聚类算法优势就在于其不需要指定类簇的个数
3.层次聚类
层次聚类通过对数据集在不同层次进行划分,从而形成树形的聚类结构。通常分类“自上而下”分拆和“自底向上”聚合两个方式。
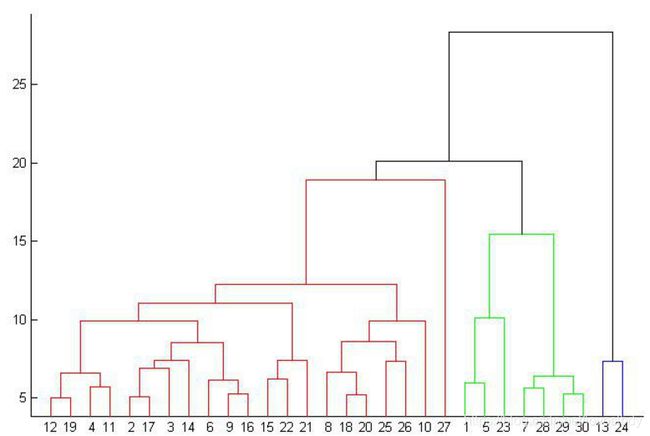
层次聚类的合并算法通过计算两类数据点间的相似性,对所有数据点中最为相似的两个数据点进行组合,并反复迭代这一过程。简单的说层次聚类的合并算法是通过计算每一个类别的数据点与所有数据点之间的距离来确定它们之间的相似性,距离越小,相似度越高。并将距离最近的两个数据点或类别进行组合,生成聚类树。计算两个组合数据点间距离的方法有三种,分别为Single Linkage,Complete Linkage和Average Linkage。
一个数据集应该聚类成多少个簇,通常和我们关注数据集的粒度相关。层次聚类算法相比划分聚类算法的优点之一是可以在不同的尺度上(层次)展示数据集的聚类情况。但是其也有缺点:(1)算法终止的条件很模糊,难以精确表达并控制算法的停止(2)一旦聚类结果形成,一般不再重新构建层次结构来提高聚类的性能。
4.谱聚类算法
谱聚类把所有的数据看做空间中的点,这些点之间可以用边连接起来。距离较远的两个点之间的边权重值较低,而距离较近的两个点之间的边权重值较高,通过对所有数据点组成的图进行切图,让切图后不同的子图间边权重和尽可能的低,而子图内的边权重和尽可能的高,从而达到聚类的目的。该算法对图论中的无向图,线性代数和矩阵分析都有涉及。
详细介绍见谱聚类
5.DBSCAN密度聚类算法
密度聚类不直接评估数据之间的相似度,将簇视为被低密度区域分隔的高密度区域。
我们定义核心样本是指数据集中的一个样本的 eps 距离范围内,存在 min_samples 个其他样本,这些样本被定为为核心样本的邻居( neighbors) 。此时,核心样本在向量空间的稠密区域。一个簇是一个核心样本的集合,可以通过递归来构建,选取一个核心样本,查找它所有的邻居样本中的核心样本,然后查找新获取的核心样本的邻居样本中的核心样本,递归这个过程。 簇中还具有一组非核心样本,它们是簇中核心样本的邻居的样本,但本身并不是核心样本。
DBSCAN的聚类定义很简单:由密度可达关系导出的最大密度相连的样本集合,即为我们最终聚类的一个类别,或者说一个簇。
sklearn代码
sklearn上关于各类对于聚类方法在不同数据下聚类效果进行了展示,具体使用调用见文档
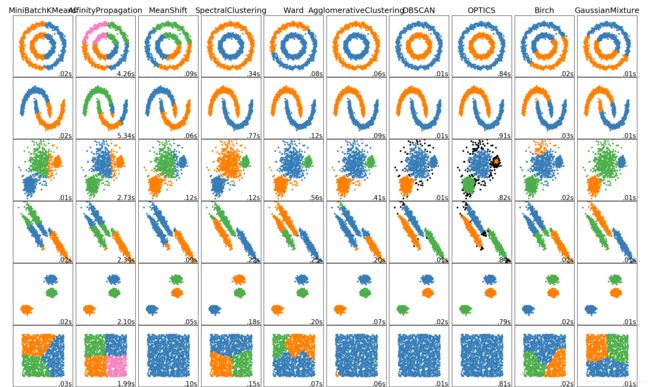
具体的代码在官网文档写的很详细,这里就不贴了。
二、潜在语义分析
这里的潜在语义分析指LSA、PLSA、LDA这三类模型。简单理解为,每篇文档包含多个主题,每篇主题下包含不同的词语。具体可以看博客。
我们首先构建一个文档-词语矩阵A,矩阵内值为词语在文档中出现的词语。
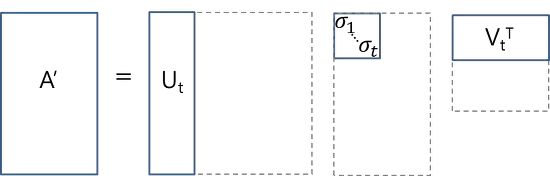
现在通过分解可以获得A’,A’和A相差不大,可以看作A’=A。Ut为各文档的主题分布,Vt为各个主题下词语的分布。
而这样分解其实解释性不强,PLSA在概率上建模,每篇文档包含多个主题,每篇主题下包含多个词语。而后又再PLSA上添加贝叶斯,得到LDA,也即主题模型。在应用场景下直接使用LDA就行。
LDA代码:
Lda = genism.models.ldamodel.LdaModel
ldamodel = Lda(doc_term_matrix, num_topics=3, id2word = dictionary, passes=50)
通过LDA来获取到了各个文档包含各个主题的概率,这个可以看作文档的低维表示进行聚类,也可以直接拿最大主题当作聚类结果。LDA使用起来也比较简单,但是它很慢。
三、深度学习聚类
按照我直观的理解,基于深度学习直接进行聚类其实是不可行的,至少是不容易的。(其损失函数怎么设定?)
常规的做法是先降维再聚类。具体可以使用神经网络进行降维,再利用传统方法在低纬空间聚类。
常见的用于降维的网络
- 自动编码机
自动编码器是一种有三层的神经网络:输入层、隐藏层(编码层)和解码层。该网络的目的是重构其输入,使其隐藏层学习到该输入的良好表征。如果训练好的模型使得输出与输入一致,那么中间少量的神经元就可以表示输入数据, 相当于可以获取输入数据的相同表示。基于这个基础、又有降噪自动编码机、稀疏自动编码机、变分自动编码器等等。我们可以基于自动编码器获取适合的数据格式,然后进行聚类。 - 受限玻尔兹曼机
受限玻尔兹曼机和自动编码器看起来类似、但是从三层变成了两层(其实应该是有巨大的差异的),在处理特征抽取的问题上,也是取其隐藏层作为原始数据的新表示。
但是我的理解错误了,其实可以完全用深度学习进行聚类
深度学习聚类网络可以分为两部分, A部分:神经网络将输入转换为新的表示,B部分:然后基于新的表示再进行聚类。
问题:深度学习做聚类其损失函数是怎么确定的,怎么训练的?(如果有一个可训练的损失函数,那么至少是可以train了)
看了一下论文Towards K-means-friendly Spaces: Simultaneous Deep
Learning and Clustering现在这里粗略的描述一下。
如果使用K-means类的聚类思路,那么网络的损失函数应该就和K-means类似
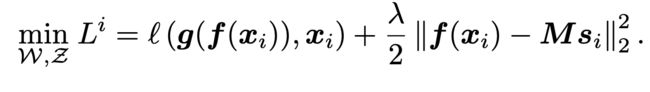
这里第一部分是论文中代表阶段A的损失,我们主要关注第二部分,也即
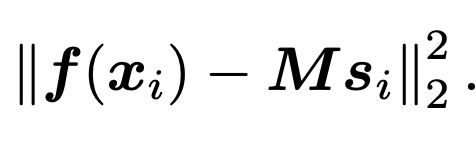
f(x)表示输入的低纬表示,M代表K个聚类中心的坐标,Si表示每个点属于哪一个类别。这里关键是Si是一个离散变量。因此这里分别训练:

具体来说:
- 固定M,S来优化网络,得到每个点的新的表示,
- 把新的点划分到各个类别(按照到中心点的远近)
- 更新每个类的中心点
和原始的K-means相比,其只是多了一个步骤1,优化对输入获取新表示的过程。
其实和我想象中的 基于深度学习聚类还是不一样的,可以说聚类这个步骤和传统思路没有区别。
我也阐述一下自己的看法:算法主要还是分为两部分,A部分学习低维表示(更适合聚类??),B部分对低维数据聚类。 其实两个任务还是分开的,但是通过目标函数的优化,可以使得学习的低维表示更适合聚类。但是聚类的这个迭代过程还是和传统方法一致。
当然,这里由于是无监督,我们不能单纯为了学习适合聚类的低维表示,也需要该低维表示可以代表原始输入(泛化能力?),所以上文公式中加入了阶段A的损失(比如自动编码器的重构误差)。这样相当于两个任务联合学习。
具体关于深度学习的聚类可以看看这篇文章Clustering with Deep Learning: Taxonomy and New Methods
下面是公众号,欢迎扫描二维码,谢谢关注,谢谢支持!
公众号名称: Python入坑NLP
本公众号主要致力于自然语言处理、机器学习、coding算法以及Python的一些知识分享。本人只是小菜,希望记录自己学习、工作过程的同时,大家一起进步。欢迎交流、分享。
