splay伸展树 指针型 平衡树基本操作 序列维护 详细讲解+总结
转载请保留本博客源地址:http://blog.csdn.net/u011327397/article/details/53783700
作者Anantheparty:http://blog.csdn.net/u011327397
本来是要去学lct,然后看到要用splay我又不会,就开始看splay了,然后发现splay 写 艹起来特别爽,但是序列操作网上没看到有详讲的,理解的时候很多奇怪的问题(无限RE)再加上指针调试复杂度高,花了很多时间,就觉得来写一个讲解吧。然后小生才疏学浅,难免会出错,如果哪位神犇看见了错误,有劳在评论区提出,THX。
文章目录
- @[toc]
文章目录
- @[toc]
#基本概念
基本概念(我的理解)还是大概说一下。
##二叉查找树
一颗符合左子树结点全部小于当前结点,右子树结点全部大于当前节点的树。
可以看出二叉查找树查找等操作的复杂度是很不稳定的,树的结构是严重影响效率的(链状的树和完全二叉树)
##平衡树
使二叉查找树维持基本平衡的数据结构,如treap,splay,sbt,AVL,红黑树(后面3个我都不会)
#splay平衡树的基本操作
##Rotate(旋转)
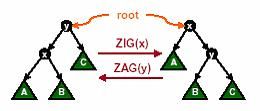
旋转看着一张图就足够了,实际上我觉得每次旋转都把这个图画出来不容易写错。。。
旋转的意思就是让我们这棵树变一下形,但是又不改变二叉查找树的规则,基本操作就是左旋和右旋,旋转的原理可以自己写出x,y,A,B,C的大小关系然后去画
我先学习的treap,因为treap不用维护父亲指针,里面的旋转超级简单,就2句话,而这里要,旋转一下就重要了。
旋转是最重要最基本的操作,一定不能记错,快速记住旋转的方法是这样的(看着上面的图):一共有3句:
B与x,y的父子关系。
y的父亲与x,y的父子关系。
x,y的父子关系。
然后每一句话对应两个操作一个是父亲指针的改变,一个是儿子指针的改变。代码如下。
void rotate(tree2 *x,int p)//p==0 left; p==1 right
{
tree2 *y=x->fa;
y->son[p^1]=x->son[p];
if(x->son[p]!=Null)x->son[p]->fa=y;//不一定有B这个儿子,要特判
y->fa->son[y->fa->son[1]==y]=x;//这是一种判断儿子方向的技巧,可以自己画一下
x->fa=y->fa;
x->son[p]=y;
y->fa=x;
pushup(y);//后面说
}
然后就是splay的旋转了,splay的旋转可以分为4种,ZIG-ZIG(右旋-右旋),ZAG-ZAG(右旋-右旋),ZIG-ZAG(右旋-左旋),ZAG-ZIG(左旋-右旋)。
(实际上是2种,相同方向和不同方向)
为什么非要分成这几个呢!!!
为什么不能直接把x一直向上转转转呢???
因为要保证复杂度,这样会让树转完变得更平衡,有一篇叫《伸展树的基本操作与应用》的论文里面有证明,我这种蒟蒻肯定看不懂,有兴趣的神犇可以去看。


对于具体的旋转这里有两张图,根据图上面树的位置关系可以手推出来怎么转,简单的说就是两个一样的方向就先转爸爸,然后自己,然后如果方向两次不一样就把自己按着该旋转的方向转上去。
##Splay(伸展)
这个是splay里面最重要的部分了(毕竟名字都是这个)不过感觉该说的都在rotate里面说完了。。
伸展就是讲一个结点通过旋转操作转到它某一个祖先下面。
主要就是上面几种旋转,然后如果只用转一次就到了特判一下
需要注意的地方就是每一个操作后面都要有splay,splay相当于是在维护树的平衡,并且使越近访问的结点越接近根,也就是说我们一直访问一个点就会很快很快,这个在OI好像没什么用,但是实际生活感觉很有用(其实我也不知道)。
代码:
void splay(tree2 *tree,tree2 *goal)//goal==null splay to the root
{
if(tree==goal)return ;
while(tree->fa!=goal)
{
if(tree->fa->fa==goal)//特判只用一次旋转
{
rotate(tree,tree->fa->son[0]==tree);//等价于rotate(tree,tree->fa->son[1]==tree^1)
break;
}
tree2 *fa=tree->fa,*gfa=fa->fa;
int x=gfa->son[1]==fa;
//旋转具体方向最好去画,比死记要好
if((tree==fa->son[1])==x)//相同方向旋转
{
rotate(fa,x^1);
rotate(tree,x^1);
}
else //相反方向
{
rotate(tree,x);
rotate(tree,x^1);
}
}
pushup(tree);
if(goal==null)root=tree;//更新根节点,容易写掉
}
##pushup
感觉一般平衡树里面只用维护结点个数,主要是按名次查询的时候用的,更多作用后面数列维护的地方讲。
void pushup(tree2 *tree)
{
tree->siz=tree->num+tree->lson->siz+tree->rson->siz;
}
##Find查找
就是根据二叉查找树的性质找数值为一个点的结点
tree2 *find_num(int k)
{
tree2 *temp=root;
while(temp->son[temp->n<k])//向下寻找结点
{
if(temp->n==k)break;
temp=temp->son[temp->n<k];
}
if(temp->n!=k)return Null;
return temp;
}
##query查询
我这里是指按名次查询,就是查询排第几的数是什么,然后这个时候我们一直维护的size就有用了,根据左右子树size的大小我们就可以一直向下走了
int query(int k)
{
tree2 *temp=root;
int num=temp->lson->siz;
while(!k==num+1)
{
if(k>num)//k>num说明在右子树
{
k-=num+1;
temp=temp->rson;
}
else temp=temp->lson;
num=temp->lson->siz;
}
splay(temp,null);//无论如何splay
return temp->n;
}
##Insert插入
这个实际上和查询差不多,就是如果没查到就创建新的结点。
void insert(int k)
{
if(root==NULL)//空树特判
{
root=newtree(null,k);
return ;
}
tree2 *temp=root;
while(temp->son[temp->n<k]!=Null)//同find
{
if(temp->n==k)//重复不添加
{
splay(temp);//无论何时都要splay
return ;
}
temp=temp->son[temp->n<k];
}
temp->son[temp->n<k]=newtree(temp,k);
splay(temp->son[temp->n<k],null);
}
##delete删除
删除要稍微复杂一点,主要是删除节点儿子的处理问题。
假设要删除的结点没有2个儿子,那就直接删除,然后把儿子接到他的父亲上就好了,然后我们来看一下2个儿子的情况。
想象一个有序数列,中间有一个数被删去了,那么原来这个数左边的数就接到了他原来这个数右边的数的最左边(或者右边的数接到了左边的最右边)
我们模拟这个操作,就找到左子树最大的一个点,因为这个点最大,它一定没有右儿子,我们就可以直接把右儿子整个接上去(因为右儿子的所有数一定大于左儿子的所有数),找最大的数就一直沿着右儿子指针向下跑就可以了。
然后实现感觉我写得有点麻烦。。。
void delet(int k)
{
tree2 *temp=find(k);
int x=temp->fa->son[1]==temp;//temp和爸爸的关系
if(temp->lson==Null)//4种情况分类讨论
if(temp->rson==Null)//无子树
temp->fa->son[x]=Null;
else //一棵子树
{
temp->fa->son[x]=temp->rson;
temp->rson->fa=temp->fa;
}
else
if(temp->rson==Null)//一棵子树
{
temp->fa->son[x]=temp->lson;
temp->lson->fa=temp->fa;
}
else//两棵子树
{
tree2 *tree=temp->lson;
temp->fa->son[x]=temp->lson;
temp->lson->fa=temp->fa;//先将左子树接到父亲上
while(tree->rson!=Null)tree=tree->rson;//寻找左子树最大点
tree->rson=temp->rson;//接上右子树
temp->rson->fa=tree;
pushup(tree);
splay(tree,null);
return ;
}
pushup(temp->fa);
splay(temp->fa,null);
}
##per前驱
##next后驱
前驱:小于当前数的最大值
后驱:大于当前数的最小值
找到一个数,然后左子树一直向右跳就是前驱,右子树一直向左跳就是后驱,然后可以写一起。
int get_num(tree2 *tree,int x)//x==0 pre; x==1 next
{
tree2 *temp=tree->son[x];
if(temp==NULL)return INF;
while(temp->son[x^1])temp=temp->son[x^1];
return abs(tree->n-temp->n);
}
##split分裂
这个和后文的数列维护删除数列差不多,就是把要分裂的部分旋转到一棵树上,然后删除,pushup,然后回收空间
##merge合并
合并有前提,就是一棵树全部元素大于另一棵树。
然后我没用过这种东西,实际上随便乱搞一下就好了,比如把大的那棵树的最小节点旋转到根,然后直接把小的那棵树接过来什么的,感觉用不到。
#splay维护序列
刚开始看这个主要是想去看看翻转,然后感觉翻转很难,然后想先看看其他序列操作,看完后在发现翻转最简单。。。
然后再在某篇文献里面看到说splay解决线段树问题要快15倍,然后就更想去看了。实际上我写的splay之比线段树快了零点几秒,不过看网上的人说splay是比线段树慢15倍我还是很开心的(万一是线段树写丑了呢233)
##基本思想
再说具体操作之前先说一下思想,理解了思想差不多后面的操作全部可以不管自己就直接靠感觉写了。
1、splay用来排序的这个时候是序号,就是那个节点在数列是第几个,所以中序遍历就是原序列,所以翻转不会有什么打乱顺序,顺序却是改变了
2、维护序列最重要的就是要找到你要维护的区间,因为区间内的数是连续的所以可以想办法弄到一颗子树上,具体操作就是这张图

我们如果要对[a,b]进行某些操作那么将树旋转成这样以后root->rson->lson就是我们要的子树了,直接对这个子树可以进行所有操作
3、splay比线段树能多做的事和优点:可以在任意数后面加入,删除,同时还有区间旋转,然后还有节省空间(splay只用O(n))的空间
4、如果只有n个结点上面的查询有着明显的问题,[1,n]该怎么查询?因此我们要增加0和n+1结点,作为哨兵结点来保护头和尾
##pushup
##pushdown
类似线段树操作,但需要注意一点,在splay里面当前节点代表的区间由左子树,自己和右子树构成,而线段树仅由左右子树,所以splay要多考虑一个自己,下面放一个求和的好了,下面的程序lazy是区间加一个值。
void pushup(tree2 *tree)
{
tree->siz=tree->lson->siz+tree->rson->siz+1;
tree->sum=tree->key+tree->lson->sum+tree->rson->sum;
}
void pushdown(tree2 *tree)
{
if(tree->lazy)//这里和线段树类似
{
tree->lson->lazy+=tree->lazy;
tree->rson->lazy+=tree->lazy;
tree->lson->sum+=(ll)tree->lson->siz*tree->lazy;
tree->rson->sum+=(ll)tree->rson->siz*tree->lazy;
if(tree->lson!=Null)tree->lson->key+=tree->lazy;
if(tree->rson!=Null)tree->rson->key+=tree->lazy;
tree->lazy=0;
}
}
##bulid建树
建树就是将这个序列按序列号大小转换成一颗二叉搜索树,我们从中间开始这棵树一来就比较平衡,降低常数(建一条链也是二叉搜索树)
然后建树很重要,用指针建树的时候一定要想清楚(不然一直RE),子树的地址是什么,先放代码:
tree2 *bulid(tree2 *fa,int l,int r)
{
if(l>r)return Null;
int mid=(l+r)>>1;
tree2 *tree=newtree(fa,a[mid]);
tree->lson=bulid(tree,l,mid-1);
tree->rson=bulid(tree,mid+1,r);
pushup(tree);
return tree;
}
这里有几点需要注意的。第一,bulid时是mid-1和线段树不同。第二,如果要让tree做参数,tree的地址就要提前赋好。
##rotate旋转
这里旋转和前面差不多其实就增加了pushup&pushdown
void rotate(tree2 *tree,int x)//x==0 left,x==1 right
{
tree2 *fa=tree->fa;
pushdown(fa);//增加语句
pushdown(tree);//增加语句
fa->son[x^1]=tree->son[x];
if(tree->son[x])tree->son[x]->fa=fa;
fa->fa->son[fa->fa->son[1]==fa]=tree;
tree->fa=fa->fa;
fa->fa=tree;
tree->son[x]=fa;
pushup(fa);
}
然后为什么最后只pushup(fa),因为splay的时候tree在下一次操作的时候还会被调用,pushup了也会立马被破坏,所以我们只用在splay结束的地方pushup一次就可以了,这样可以减小常数
##splay伸展
splay和前面完全一样,pushdown都在rotate里面了,省略。
##splayto按序号伸展
我乱起的名字,我也不知道叫什么,中英文都不知道。。
理解成将在原序列中编号为k的旋转到它的某个祖先下面
实际上就是一个查询+splay查询和上面的query 基本一样,
void splayto(int k,tree2 *goal)
{
tree2 *tree=root;
pushdown(tree);
int num=tree->lson->siz;
while(num!=k)//这里上面是num+1
{
if(num<k)
{
tree=tree->rson;
k-=num+1;
}
else tree=tree->lson;
pushdown(tree);
num=tree->lson->siz;
}
splay(tree,goal);
}
造成这种差异是哨兵元素(在基本思想最后一个提了一句),导致多了0号结点。
##Insert插入
在pos后面插入一个数或者一段数,这个是splay特有的,线段树做不到,思想很简单,就把pos转到根,然后pos+1转到根的右儿子(新加入的数序号肯定在原pos和pos+1之间),然后把要加入的数列建一棵树加在pos+1的左儿子。
void insert(int pos,int num)//这里是加一段数,num是数的个数
{
if(num==0)return ;
for(int i=1;i<=num;i++)
a[i]=read();
splayto(pos,null);//pos转到根
splayto(pos+1,root);//pos+1到root->rson
key=bulid(root->rson,1,n);//key是root->rson->lson后同
pushup(root->rson);
pushup(root);
}
##delete删除
删除还是一样,先把要删除区间转到key(见上文代码注释),然后直接删除,回收空间就好了
void delet(int pos,int num)
{
if(num==0)return ;
splayto(pos-1,null);
splayto(pos+num,root);
rec(key);//回收空间
key=Null;//删除
pushup(root->rson);
pushup(root);
}
##addnum区间修改
这里用区间加一个数来举例子,其他区间修改类似线段树。
还是先把区间找到,然后直接修改就好了,没什么好多说的
void add(int l,int r,int num)
{
splayto(l-1,null);
splayto(r+1,root);
key->lazy+=num;
key->sum+=(ll)num*key->siz;
key->key+=num;
}
##reserve旋转
旋转实际上和上面的修改差不多,只是pushdown有点不一样。
一个区间如果旋转2次就又转回来了,所以我们直接异或1就好了
void reverse(int l,int r)
{
if(num==0)return ;
splayto(l-1,null);
splayto(r+1,root);
key->f^=1;
swap(key->lson,key->rson);
swap(key->lx,key->rx);
pushup(root->rson);
pushup(root);
}
void pushdown(tree2 *tree)
{
if(tree->f)
{
tree->lson->f^=1;
tree->rson->f^=1;
swap(tree->lson->lson,tree->lson->rson);
swap(tree->rson->lson,tree->rson->rson);
tree->f=0;
}
}
##sum求和
求和类似线段树,pushup实际上就是我上面放那个
##print输出数列
直接中序遍历输出就好了,要特判哨兵不输出(我下面没有特判)。
然后记得pushdown。
void print(tree2 *tree)
{
pushdown(tree);
if(tree->lson!=Null)print(tree->lson);
printf("%d ",tree->n);
if(tree->rson!=Null)print(tree->rson);
}
#基础训练题目
后面都是一些裸题,可以用来上手。
我写得都比较长(不习惯压码),但自认为可读性和速度还是可以
##【bzoj1588】 [HNOI2002] 营业额统计
基本平衡树操作,只有insert和查询前驱后驱
#include##【poj3468】 A Simple Problem with Integers
这个是线段树经典题目了,区间修改,区间求和。splay做起来实际上要复杂得多,不过2797MS比我大线段树3063MS要快了一点点
#include##【bzoj3223】 Tyvj 1729 文艺平衡树
这个就一个旋转。。
#include##【bzoj3224】 Tyvj 1728 普通平衡树
一颗基本平衡树的各种操作,打完当板用的题
#include##【bzoj1500】 [NOI2005]维修数列
这个题就是全部的序列维护了,vijos上有一道小白逛公园和这个有点像,就是求区间最大子序列,不过那个是线段树,没有翻转,还有一个加强版就是序列变成一棵树,变成树剖,这个就还加了一大堆操作。
然后维护的时候要维护区间和(sum),区间长度(siz),区间最大子序列(mx),从左边起区间最大子序列(lx),从右边起区间最大子序列(rx),还有翻不翻转(f)
pushup和pushdown要尤其小心
#include#易错内容
1、题目读入大多带负数,读入优化要加负数
2、严格注意哨兵结点的修改是否会影响树
3、splay最后还要pushup(tree)
4、建树不可以把儿子指针直接放到参数上面!!!
5、再向下找第k个结点的时候num要在循环末附上新的值,并且要记得pushdown
6、序列操作完了以后要pushup,平衡树所有操作完了一定要splay,不然可能T
7、如果有多种有标记的操作,应该在给结点打标记的时候修改它,而不是pushdown的时候,pushdown应该去修改它的儿子
8、求最值哨兵结点不要直接赋0
9、修改关系要2部操作,修改son和fa指针
#总结
splay是一个很强大写起来也比较舒服的数据结构,并且内存要求也不高,相对于其他平衡树和线段树都有比较大的优势
#参考资料
《伸展树的基本操作与应用》:我实际上就用了里面三张图