K近邻模型、KNN算法1-构建预测模型

K近邻模型、KNN算法1-构建预测模型

案例

假设你已经清洗好了一份同类型的商品信息和价格数据，如果给一个同品类全新的商品，你如何给它定价或预测它的价格？

比如，这个商品是红酒。你已经获取到了一批红酒的评级、生产年份、瓶装大小等红酒属性数据，以及对应的红酒价格。现在请根据这个样本数据对一瓶红酒进行价格预测、价格区间概率预测。

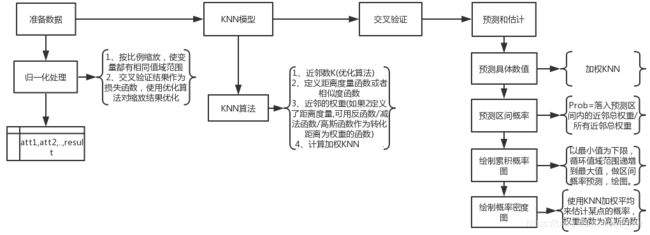
思路逻辑图

Python代码

#!/usr/bin/env python
# -*- coding: utf-8 -*-
#@Time: 2019-11-18 07:07
#@Author: gaoll

import time
import random
from random import randint
import math
import numpy as np
import matplotlib.pyplot as plt

#定义距离函数. 
def euclidean(v1,v2):
	d = 0.0
	for i in range(len(v1)):
		d+=(v1[i]-v2[i])**2
	return math.sqrt(d)

#计算距离。KNN算法距离计算完保存起来，使用时无需再计算
def getdistances(data,vec1,distance=euclidean):
	distancelist = []
	for i in range(len(data)):
		vec2=data[i]['input']
		d = distance(vec1,vec2)
		distancelist.append((d,i))
	distancelist.sort()
	return distancelist

#定义权重公式
#反函数
def inverseweight(dist,num=1.0,const=0.1):
	return num/(dist+const)
#减法函数
def substractweight(dist,const=1.0):
	if dist>const:
		return 0 
	else:
		return const - dist
#高斯函数
def gaussian(dist,sigma=10.0):
	return math.e**(-dist**2/(2*sigma**2))

#创建KNN函数，根据前k项估计,加权knn
def createweightedknn(k,weighf=gaussian):
	def weightedknn(data,vec1):
			#按照距离值经过排序的列表
		dlist = getdistances(data,vec1)
		avg = 0
		total_weight = 0.0
		for i in range(k):
			(dist,id) = dlist[i]
			weight = weighf(dist)
			avg+=data[id]['result']*weight
			total_weight += weight
		avg = avg/total_weight
		return avg
	return weightedknn

#交叉验证--拆分测试集和训练集
def dividedata(data,test=0.05):
	trainset = []
	testset = []
	for row in data:
		if random.random()=low and v<=high:
			inweight += weight
		totalweight += weight
	if inweight == 0:
		return 0
	return inweight/totalweight

#根据区间概率预测，绘制累计概率图
def cumulativegragh(data,vec1,high,k=3,weightf=gaussian):
	x = np.arange(0.0,high,0.1)
	y = [probguess(data,vec1,0.0,t,k=k,weightf=weightf) for t in x]
	fig = plt.figure()
	ax=fig.add_subplot(1,1,1)
	ax.plot(x,y)
	fig.show()

#使用KNN思想，绘制概率密度图
def probalitygragh(data,vec1,high,k=3,weightf=gaussian,ss=5.0):
	x = np.arange(0.0,high,0.1)
	#得到每个小区间上的概率
	probs = [probguess(data,vec1,v,v+0.1,k,weightf) for v in x]
	#做平滑处理，即加上近邻概率的高斯权重
	smoothed = []
	for i in range(len(probs)):
		sv = 0.0
		for j in range(0,len(probs)):
			dist = abs(i-j)*0.1
			weight = weightf(dist,sigma=ss)
			sv+=weight*probs[j]
		smoothed.append(sv)
	fig = plt.figure()
	ax = fig.add_subplot(1,1,1)
	ax.plot(x,smoothed)
	fig.show()



if __name__ == "__main__":
	#记载数据
	import wineprice
	data = wineprice.wineset3()

	#优化K，确定K的大致范围,这里设2-7
	costf_k = createcostf_k(data,createweightedknn)
	for i in range(2,8):
		print(i,costf_k(i))

	'''out：从简单从小，这里k=4交叉验证损失最小
	2 62368.44691765818
	3 66027.43378150972
	4 61087.78286215031
	5 65923.3855665127
	6 67817.68744348118
	7 67395.5927600834
	'''
	#以上述得出的k=4为基础，优化scale
	import optimization 
	weightedknn = createweightedknn(k=4)
	domain = [(0,20)]*4
	costf_scale = createcostf_scale(weightedknn,data)
	#使用模拟退火算法优化缩放系数。--见前面的博文-优化算法
	optimization.annealingoptimize(domain,costf_scale)
	#Out[150]: [1, 13, 12, 0]

	#K和放缩比例相互影响，这个确定的过程比较繁琐，可能要重复几次。
	#这里经过3次相互交叉验证后，决定使用 k=3,scale=[8, 4, 3, 2]。
	k = 3
	scale = [8, 4, 3, 2]

	scaled_data = rescale(data,scale)
	weightedknn = createweightedknn(k=3,weighf=gaussian)
	#交叉验证
	crossvalidate(weightedknn,scaled_data)
	#Out[153]: 62935.15164770742

	#knn数值预测
	TobePredict=[90, 35, 13, 3000.0]
	scaled_tobepredict = rescale_vec(TobePredict,scale) #放缩
	print(weightedknn(scaled_data,scaled_tobepredict))  #预测
	#188.3792652896066

	#价格区间预测
	probguess(scaled_data,scaled_tobepredict,100,150)
	#Out[106]: 1.2491095402673855e-05
	probguess(scaled_data,scaled_tobepredict,100,180)
	#Out[107]: 0.3000429516680889
	probguess(scaled_data,scaled_tobepredict,100,200)
	#Out[108]: 1.0

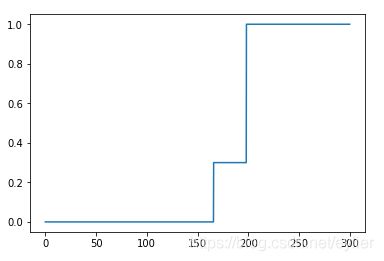
	#累计概率图
	cumulativegragh(scaled_data,scaled_tobepredict,300)

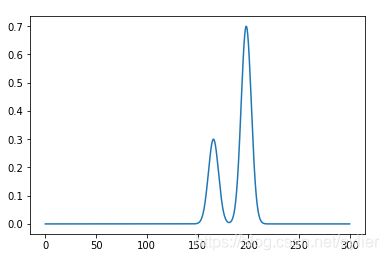
	#概率密度图
	probalitygragh(scaled_data,scaled_tobepredict,300)
    

结果展示

#1、累计概率图

#2、概率密度图（从概率密度图中发现它的概率分布并不对称，说明有可能我们的数据中存在未知的隐藏变量，需要再详细询问获取的数据是否有漏标记说明的信息。）