THE WISDOM OF THE CROWD: RELIABLE DEEP REINFORCEMENT LEARNING THROUGH ENSEMBLES OF Q--FUNCTIONS

ABSTRACT

Reinforcement learning agents learn by exploring the environment and then ex-ploiting what they have learned. This frees the human trainers from having to know the preferred action or intrinsic value of each encountered state. The cost of this freedom is reinforcement learning is slower and more unstable than su-pervised learning. We explore the possibility that ensemble methods can remedy these shortcomings and do so by investigating a novel technique which harnesses the wisdom of the crowds by bagging Q-function approximator estimates.

Our results show that this proposed approach improves all three tasks and rein-forcement learning approaches attempted. We are able to demonstrate that this is

adirect result of the increased stability of the action portion of the state-action-value function used by Q-learning to select actions and by policy gradient methods to train the policy.
强化学习代理通过探索环境然后开发他们学到的东西来学习。 这使得人类训练员不必知道每个遇到状态的优选动作或内在值。 这种自由的代价是强化学习比经验教学更慢，更不稳定。 我们探索了集合方法可以弥补这些缺点的可能性，并通过调查一种利用Q函数近似估计来利用人群智慧的新技术来实现这一点。

我们的结果表明，这种提出的方法改进了所有三项任务和尝试的强制学习方法。 我们能够证明这是

Q学习用于选择行动的状态 - 行动 - 价值函数的行动部分的稳定性增加的直接结果，以及通过政策梯度方法来训练政策。

1INTRODUCTION

In the reinforcement learning (RL) approach the agent learns by exploring its environment and the, sometimes, many approaches to solving a given problem. It frees the human trainers from having to know the preferred action or intrinsic value of each encountered state. There is no denying that RL has a grassroots feel: it is an important form of learning in the natural world and it is only natural that machine learning practitioners would want to mimic its success.

This freedom comes at a price, however. The most common complaints about RL, especially when using function approximators to learn Q-functions, are that RL is too slow and unstable during learn-ing. Learning by exploration of the environment results in a training signal which is less informative than a supervised training signal resulting in the requirement of a large number of training samples and repeated exposure to those samples. The proposed approach is an ensemble learning approach to RL similar to the well-known bagging approach, Breiman (1996), which trains ensemble members using the experience replay memory and combines their action selections using voting or averaging.
在强化学习（RL）方法中，代理通过探索其环境以及有时解决给定问题的许多方法来学习。它使人类培训师不必知道每个遇到状态的首选动作或内在价值。无可否认，RL有一种基层的感觉：它是自然界中一种重要的学习形式，机器学习从业者想要模仿它的成功是很自然的。

然而，这种自由是有代价的。关于RL的最常见的抱怨，特别是当使用函数逼近器来学习Q函数时，RL在学习期间太慢且不稳定。通过探索环境来学习导致训练信号，其比监督的训练信号信息量小，导致需要大量训练样本并重复暴露于那些样本。所提出的方法是RL的集合学习方法，类似于众所周知的装袋方法，Breiman（1996），其使用经验重放记忆训练合奏成员并且使用投票或平均来组合他们的动作选择。

1. RECENT ADVANCEMENTS IN RL

There has been tremendous advancements in RL in recent years spurred by the excitement sur-rounding deep Q-learning (DQN), Mnih et al. (2015). Impressively, RL has featured prominently in published work showing super-human performance in tasks which were previously considered un-touchable by state of the art RL approaches just a few years ago. These include RL agents playing chess at a grand-master level, Lai (2015), and the famous AlphaGo, Silver et al. (2016). Through this work we have found just how far we can go when applying existing RL approaches with large amounts of computing power.

A large effort has been devoted to addressing the RL obstacle of slow learning, Mnih et al. (2016); Schaul et al. (2016), with an emphasis on speeding-up RL for the high-dimension inputs popularized by the DQN work – especially since DQN exacerbated this issue both in terms of the required com-putation and number of training time steps. There has also been work showing other RL approaches can be adapted to the DQN paradigm, Lillicrap et al. (2016).
For all of these recent works mentioned here the primary emphasis is achieving improved perfor-mance on simulated tasks in the shortest amount of wall-clock time. The issues of RL instability during training and of reducing the number of interactions with the training environment have re-ceived little attention. The crowd ensemble addresses the obstacle of training instability without sacrificing the number of interactions with the training environment which, in many real-world ap-plication, may be more expensive than the computational costs. Furthermore, the crowd ensemble method can be used alongside any of these recent advances in RL.
近年来，由于围绕深度Q学习（DQN）的激动，Mnih等人在RL中取得了巨大的进步。 （2015年）。令人印象深刻的是，RL在已发表的作品中占据突出地位，展示了几年前最先进的RL方法无法触及的任务中的超人类表现。这些包括RL代理人在大师级别下棋，Lai（2015），以及着名的AlphaGo，Silver等人。 （2016）。通过这项工作，我们发现在应用具有大量计算能力的现有RL方法时我们能走多远。

Mnih等人致力于解决缓慢学习的RL障碍。 （2016）; Schaul等人。 （2016），重点是加快由DQN工作推广的高维输入的RL - 特别是因为DQN在所需的计算和训练时间步数方面加剧了这个问题。还有一些工作表明其他RL方法可以适用于DQN范例，Lillicrap等。 （2016）。
对于这里提到的所有这些最近的工作，主要的重点是在最短的挂钟时间内实现模拟任务的改进性能。训练期间RL不稳定以及减少与训练环境的相互作用的问题几乎没有引起人们的注意。人群集合解决了训练不稳定性的障碍，同时又不牺牲与训练环境的交互次数，在许多现实世界的应用中，这可能比计算成本更昂贵。此外，人群集合方法可以与RL中的任何这些最新进展一起使用。

1. THE WISDOM OF CROWDS

Francis Galton, in 1906, observed that a large group’s mean guess was able to come within one pound when guessing the weight of an Ox, Galton (1907). This was surprising because the crowd, while containing a few potential experts, was presumably made of non-experts with no knowledge of estimating the weight of oxen.

More recently Treynor (1987) emphasizes the need for independence of the individual to the success of the crowd and that allowing sources of shared error or bias will reduce the accuracy of a crowd’s prediction. He concludes that chasing an expert is folly and that a simple combination of crowd information is best. Larrick & Soll (2006) and Hastie & Kameda (2005) emphasize the power of averaging predictions. Appropriate use of averaging in group decisions begins with understanding that averaging is not a regression to the mean but, rather, an error-reduction technique

Surowiecki (2005) synthesizes the many benefits of crowd-based decision-making. Although the crowd will not regularly out-perform the best individual, no field can provide a mechanism to predict which individual will out-perform the crowd. Fortunately, many of the obstacles to quality crowd decision-making are a result of the shortcomings and complexities of human group dynamics are not problems we encounter when training Q-function ensembles.
弗朗西斯·高尔顿（Francis Galton）于1906年观察到，当猜测牛的重量时，一个大群体的平均猜测能够在一磅之内，高尔顿（1907）。这是令人惊讶的，因为人群虽然包含一些潜在的专家，但可能是由非专家组成，不知道估计牛的重量。

最近，Treynor（1987）强调了个体对人群成功的独立性的必要性，并且允许共享错误或偏见的来源将降低人群预测的准确性。他的结论是，追逐专家是愚蠢的，人群信息的简单组合是最好的。 Larrick＆Soll（2006）和Hastie＆Kameda（2005）强调平均预测的力量。在群体决策中适当使用平均值首先要了解平均值不是平均值的回归，而是减少误差的技术

Surowiecki（2005）综合了基于群体的决策制定的诸多好处。虽然人群不会经常表现出最好的个人，但没有一个领域可以提供一种机制来预测哪个人会胜过人群。幸运的是，质量人群决策的许多障碍是人类群体动力学的缺点和复杂性的结果，这不是我们在训练Q-功能集合时遇到的问题。

2 RELATED WORK

Most ensemble RL methods fit the mixture of experts paradigm described in Jacobs et al. (1991). A Gaussian mixture model approach is utilized as the ensemble mechanism by Agostini & Celaya (2011). This gives each ensemble member a region of expertise. They test their approach on the pen-dulum swing-up and cart-pole balancing tasks. An couple ensembles of ANN Q-function approx-imators are compared in a limited set of experiments on the pole-balancing task in Hans & Udluft (2010). They conclude that a hard combination of ensemble members, that is only one expert is active at a time, is superior to the soft-combination of experts they initially attempted.

In the multiple model reinforcement learning (MMRL), Doya & Samejima (2002), approach each expert has a forward model and a Q-function. The forward models determine how to combine member outputs and how to backpropogate the error signals. In Doya & Samejima (2002) MMRL is tested on the non-stationary pendulum swing-up task. For these experiments they are forced manually partition the state space.

In Faußer & Schwenker (2015) a concept very similar to the crowd ensemble method is proposed. Their approach has an important difference: the ensemble members are trained in parallel with each other. This results in a factor of NE more interactions with the training environment. Their results show that their approach with NE > 3 performs better than a single Q-learner on a maze navigation task and a simplified tetris task (SZ-tetris) with a reduced set of pieces. No explanation is given for the improved performance of the ensemble.

Recently Q-learning approaches have been developed which resemble ensemble methods and may share some of the same benefits. These approaches are not ensembles because they do not have a mechanism which combines ensemble member outputs.

Mnih et al. (2016) and Nair & Silver (2015) present a RL approach which uses multiple, simultane-ous simulations to speed-up DQN. In Mnih et al. (2016) this method is called asynchronous DQN. True to its name, the parameter updates are not synchronized allowing each simulation to period-ically update the global parameter values using an accumulated gradient over several time steps. Asynchronous DQN is tested using a large number of arcade learning environment.
Double Q-learning, Hasselt (2010). is designed to address the issue of over estimation of Q-values. This is done by leveraging two Q-functions. In a later work the double Q-learning concept is adapted to the DQN framework van Hasselt et al. (2015). The double Q-learning concept is taken a step further by investigating using any number of Q-learners which they call multi Q-learning, Duryea (2016).
大多数整体RL方法符合Jacobs等人描述的专家范例的混合。 （1991年）。高斯混合模型方法被Agostini＆Celaya（2011）用作集合机制。这为每个合奏成员提供了专业领域。他们在笔杆摆动和推车杆平衡任务上测试他们的方法。在Hans＆Udluft（2010）的杆极平衡任务的有限实验中，比较了几个ANN Q函数近似器的集合。他们的结论是，一次只有一名专家的合奏成员的硬组合优于他们最初尝试的专家的软组合。

在多模型强化学习（MMRL），Doya＆Samejima（2002）中，每个专家的方法都有正演模型和Q函数。正向模型确定如何组合成员输出以及如何反向传播误差信号。在Doya＆Samejima（2002）中，MMRL在非平稳摆锤摆动任务上进行了测试。对于这些实验，他们被迫手动分区状态空间。

在Faußer＆Schwenker（2015）中，提出了一种非常类似于人群集合方法的概念。他们的方法有一个重要的区别：合奏成员彼此平行训练。这导致NE与训练环境的更多交互因素。他们的结果表明，NE> 3的方法在迷宫导航任务和简化的俄罗斯方块任务（SZ-tetris）上的表现优于单个Q学习者。对于整体的改进性能没有给出解释。

最近开发了类似于集合方法的Q学习方法，并且可以分享一些相同的益处。这些方法不是合奏，因为它们没有组合整体成员输出的机制。

Mnih等人。 （2016）和Nair＆Silver（2015）提出了一种RL方法，该方法使用多个同时模拟来加速DQN。在Mnih等人。 （2016）这种方法称为异步DQN。与其名称相反，参数更新不同步，允许每个模拟使用多个时间步长的累积梯度周期性地更新全局参数值。异步DQN使用大量的街机学习环境进行测试。
双Q学习，Hasselt（2010）。旨在解决Q值过高估计的问题。这是通过利用两个Q函数来完成的。在后来的工作中，双Q学习概念适用于van Hasselt等人的DQN框架。 （2015年）。双Q学习概念更进一步，通过调查使用他们称之为多Q学习的任意数量的Q学习者，Duryea（2016）。

3METHOD

Here we briefly describe the crowd ensemble approach to Q-learning and the experiments used to evaluated the proposed method. We begin with the crowd ensemble.
在这里，我们简要描述了Q-learning的人群集合方法和用于评估所提方法的实验。 我们从人群合奏开始。

3.1 THE CROWD ENSEMBLE APPROACH TO Q-LEARNING

Q-learning, Sutton & Barto (1998), learns a state-action function, Q(s, a) which is updated according to:

Prior to learning, the Q-function approximator parameters for each expert should be randomly ini-tialized. Learning in a crowd ensemble follows these steps.

1.Vote: select an action for each expert.

2.Tally: determine which action is selected by the most members.

3.Act: take the action selected by the ensemble.

4.Observe: store the new state and store it in the experience replay memory.

5.Sample: independently sample from the experience replay memory for each member.

6.Compute errors: compute a TD-error for each member.

7.Update: update Q-function approximations using each member’s TD-error.

Our implementation of a Q-learning crowd ensemble is described in greater detail in Algorithm 1. In our experiments no new hyper-parameter search is conducted when applying a crowd ensemble: the parameters found via a manual search for the baseline approaches are also used for the crowd ensemble members.

在学习之前，应该随机初始化每个专家的Q函数逼近器参数。 在人群中学习遵循这些步骤。

1.投票：为每位专家选择一个动作。

2.Tally：确定大多数成员选择的动作。

3.Act：采取整体选择的动作。

4.Observe：存储新状态并将其存储在体验重放存储器中。

5.Sample：从每个成员的经验重播记忆中独立采样。

6.计算错误：计算每个成员的TD错误。

7.更新：使用每个成员的TD错误更新Q函数近似值。

我们在算法1中更详细地描述了Q学习人群集合的实现。在我们的实验中，在应用人群集合时没有进行新的超参数搜索：通过手动搜索基线方法找到的参数也用于 人群合奏成员。

4EXPERIMENTS

The purpose of the cart-pole task is to start a trial with the agent’s pole in the down position and allow the agent to move the cart back and forth along a 2-D track in order to swing the pole up and balance it. The track is of finite length and each end of the track has a wall with which the cart interacts via elastic collisions. The cart-pole task has four state variables: cart position, cart velocity, pole angle, and pole angular velocity. The actions are discrete with a ∈ {−1, 0, 1} which translate to push left, no push, and push right. The agent is rewarded a negative one when pointing downward, a positive one when pointing upward, and zero elsewhere.
We approximate a Q-function using an ANN with a single hidden layer with 20 nodes. The ANN inputs are the four state dimensions and scalar action value. The ANN output is the associated Q(s, a) value. The parameters are updated using scaled conjugate gradient, Møller (1993). We store all experiences and sample them in batches of 1000 for each update. We update the parameters using five batches every 1000 time steps during training. The training simulation is run continuously and is never reset. Evaluation is performed using a separate simulation which is reset for each evaluation.

We also evaluate using a high-dimension state representation of the cart-pole task where the state is represented by two consecutive frames of an image of the cart-pole environment. The approach is similar to the DQN approach described in Mnih et al. (2015). The ANN has two convolutional and two fully-connected layers. No batch normalization layers are used. The convolutional layers use ReLU activation functions while the fully-connected layers use tanh. The convolutional layers have 20 and 40 features, respectively. The window size of the first convolutional layer is 6 × 6 and the second is 4 × 4. The strides for both layers is 2 × 2 meaning a new window starts every two pixels in both directions leading to overlap of the windows. The fully-connected layers are of size 100 and 20, respectively. The parameters are updated using ADAM, Kingma & Ba (2015).

The DQN approach requires a large number of parameters so we share the convolutional layers between the ensemble members. This is done by accumulating the gradient from the fully-connected layers of all ensemble members and using it update the shared convolutional layers.

When applying the crowd ensemble via DQN the same cart-pole simulation is used by the inputs are two sequential frames of the simulation. These can be seen in Section 8.3 along with some example features extracted by the CNN.

We also apply the crowd ensemble approach to the continuous state-action bipedal walker task, team (2016), via the DDPG algorithm which is a actor-critic approach, (Sutton & Barto, 1998, 69). The bipedal walker task objective is to train an agent to move a simple bipedal robot across a two-dimension, set-width, gently sloping, plane. The robot consists of two legs and an oblong hull which sits on top of the legs. The action space is continuous in four dimensions: the actuations for the hip and knee in each leg of the robot. The state space is represented in 24 dimensions: hull angle, hull angular velocity, hull x velocity, hull y velocity, leg one hip angle, leg one hip speed, leg one knee angle, leg one knee velocity, leg one ground contact indicator (boolean), leg two hip angle, leg two hip speed, leg two knee angle, leg two knee velocity, leg two ground contact indicator (boolean), and ten lidar measurements measuring the distance to the ground from the center of the hull from ten different angles. The reward function is designed to reward forward motion with minimal motor actuation while encouraging the agent to keep the hull from pointing downward and severely penalizing the agent if the hull touches the ground. The task is considered solved if the entire course is traversed within the allocated amount of time with a total reward greater than 300.

The parameters used for training the actor and critic ANNs for the bipedal walker were taken from the supplementary material of Lillicrap et al. (2016). DDPG views the actor outputs as defining the mean of a Normal distribution with unit variance. Combining the output of multiple actors using averaging will, most likely, result in a location of exceedingly small probability. Furthermore actor outputs will be multi-modal in four dimensions which will result in a challengingly large number of modes for which no straight-forward method to find the highest-probability location exists. Instead the crowd ensemble approach is applied to DDPG by training a single actor from the combined output of a crowd ensemble of critics.
推车杆任务的目的是在座椅杆处于向下位置的情况下开始试验，并允许座椅沿着2-D轨道来回移动推车，以使杆向上摆动并平衡它。轨道具有有限的长度，并且轨道的每个末端具有壁，推车通过弹性碰撞与该壁相互作用。推车杆任务有四个状态变量：推车位置，推车速度，杆角和杆角速度。动作是离散的，∈{-1,0,1}转换为向左推，无推，向右推。当指向下方时，代理被奖励为负数，当指向上方时，奖励为正，而在其他地方则为零。
我们使用具有20个节点的单个隐藏层的ANN来近似Q函数。 ANN输入是四个状态维度和标量动作值。 ANN输出是相关的Q（s，a）值。使用缩放共轭梯度更新参数，Møller（1993）。我们存储所有经验，并在每次更新时以1000个批量对其进行抽样。我们在培训期间每1000个步骤使用五个批次更新参数。训练模拟连续运行，永不复位。使用针对每个评估重置的单独模拟来执行评估。

我们还使用推车杆任务的高维状态表示来评估，其中状态由推车杆极环境的图像的两个连续帧表示。该方法类似于Mnih等人描述的DQN方法。 （2015年）。 ANN具有两个卷积层和两个完全连接层。不使用批量标准化层。卷积层使用ReLU激活函数，而完全连接的层使用tanh。卷积层分别具有20和40个特征。第一卷积层的窗口大小是6×6，第二卷积是4×4。两个层的步幅是2×2，意味着新窗口在两个方向上每两个像素开始，导致窗口重叠。完全连接的层分别为100和20。使用ADAM，Kingma＆Ba（2015）更新参数。

DQN方法需要大量参数，因此我们共享集合成员之间的卷积层。这是通过累积来自所有集合成员的完全连接层的梯度并使用它来更新共享卷积层来完成的。

当通过DQN应用人群集合时，输入使用相同的车竿模拟是模拟的两个连续帧。这些可以在8.3节中看到，以及CNN提取的一些示例特征。

我们还通过DDPG算法将人群集合方法应用于连续状态 - 行动双足步行者任务团队（2016），这是一种演员 - 评论家方法（Sutton＆Barto，1998,69）。双足步行者任务的目标是训练一个特工将一个简单的双足机器人移动到一个二维的，宽度设置的，平缓倾斜的平面上。机器人由两条腿和一条长圆形船体组成，船体位于腿的顶部。动作空间在四个维度上是连续的：机器人每条腿的髋部和膝部的动作。状态空间以24维表示：船体角度，船体角速度，船体x速度，船体y速度，腿部一个臀部角度，腿部一个臀部速度，腿部一个膝盖角度，腿部一个膝盖速度，腿部一个地面接触指示器（ boolean），腿部两个臀部角度，腿部两个臀部速度，腿部两个膝盖角度，腿部两个膝盖速度，腿部两个地面接触指示器（布尔值），以及十个激光雷达测量距离船体中心距离地面的距离十不同的角度。奖励功能旨在以最小的马达驱动来奖励前进运动，同时鼓励代理人保持船体不向下指示并且如果船体接触地面则严重惩罚代理人。如果整个课程在分配的时间内遍历并且总奖励大于300，则该任务被认为已解决。

用于训练双足步行者的演员和评论人工神经网络的参数来自Lillicrap等人的补充材料。 （2016）。 DDPG将actor输出视为定义具有单位方差的Normal分布的均值。使用平均值组合多个参与者的输出很可能会导致概率非常小的位置。此外，演员输出将是四维的多模态，这将导致具有挑战性的大量模式，对于这些模式，不存在找到最高概率位置的直接方法。相反，人群集合方法适用于DDPG，通过从一群批评者的综合输出中训练一个演员。

5 RESULTS

The cart-pole tasks benefits from the crowd ensemble approach as shown in Figure 1 which shows that the mean reward during evaluation is improved when using any size ensemble with no significant improvement after NE = 5 where NE is the ensemble size. The improved stability is evident in Figure 2 which shows four randomly-selected runs of the ensemble with NE = 50 and four non-ensemble run. All selected non-ensemble runs show catastrophic forgetting while this happens in none of the ensemble examples.

Figure 1b shows that the ensemble approach solves the task earlier and more reliably than the non-ensemble approach. In this figure, all crowd ensemble agents solve the task within 1.7 × 105 time steps while 29 of 30 base Q-learners solve the task by 3 × 105.
如图1所示，推杆极限任务受益于人群集合方法，其显示在使用任何尺寸集合时评估期间的平均奖励在NE = 5之后没有显着改善，其中NE是整体尺寸。 图2中显示了改进的稳定性，其显示了随机选择的四个NE = 50和四个非整体运行的整体运行。 所有选定的非集合运行都会显示灾难性遗忘，而这种情况并非在任何集合示例中发生。

图1b显示了集成方法比非集合方法更早，更可靠地解决了任务。 在该图中，所有人群集合代理在1.7×105时间步骤内解决任务，而30个基础Q学习者中的29个以3×105解决任务。

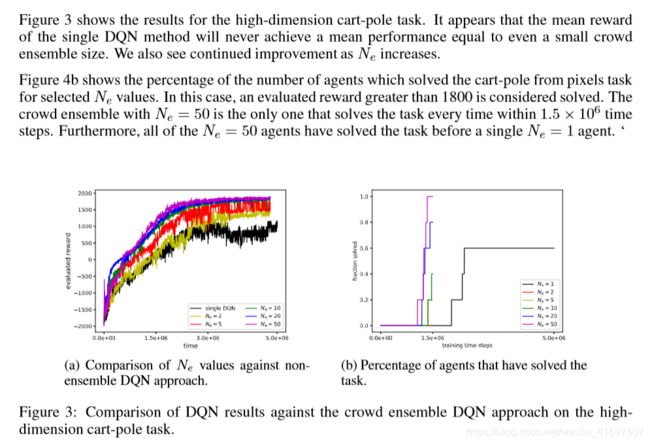
图3显示了高维推车杆任务的结果。 似乎单个DQN方法的平均奖励永远不会达到甚至小人群整体大小的平均表现。 随着NE增加，我们也看到持续改善。

图4b显示了从所选NE值的像素任务中解决了极点的代理数量的百分比。 在这种情况下，认为大于1800的评估奖励被解决。 NE = 50的人群集合是唯一一个在1.5×106时间步长内每次解决任务的人。 此外，所有NE = 50个代理已经在单个NE = 1代理之前解决了该任务。“

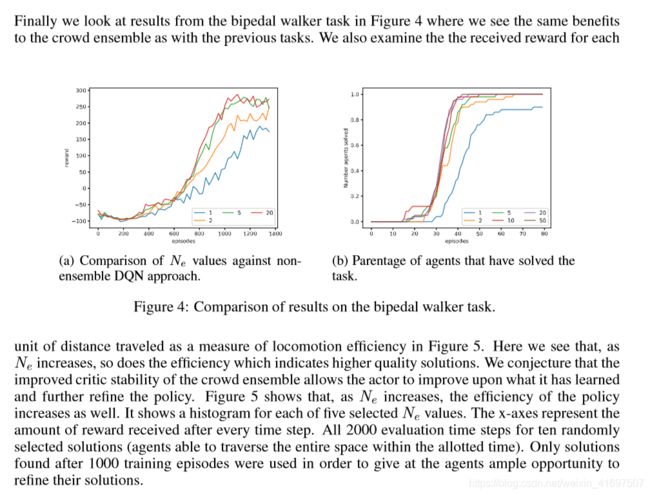
在图5中，作为运动效率的度量，行进的距离单位在这里我们看到，随着NE增加，效率也表示更高质量的解决方案。 我们推测，人群集体的批评稳定性得到改善，可以让行为者改进所学知识并进一步完善政策。 图5显示，随着NE的增加，政策的效率也会提高。 它显示了五个选定NE值中每一个的直方图。 x轴表示每个时间步之后收到的奖励金额。 所有2000个评估时间步长为10个随机选择的解决方案（能够在规定的时间内遍历整个空间的代理）。 仅使用1000次训练后发现的解决方案，以便为代理商提供充分的机会来完善他们的解决方案。

The decision space is dominated by a boundary between the push left and push right decisions which runs diagonally through this 2-dimension cross-section of the space. The Q-function is dominated by a ridge of high Q-values which also runs diagonally across the center of the decision boundary.
决策空间由推左和推右决策之间的边界支配，该边界沿对角线穿过该空间的二维横截面。 Q函数由高Q值的脊支配，该Q值也沿决策边界的中心对角线运行。

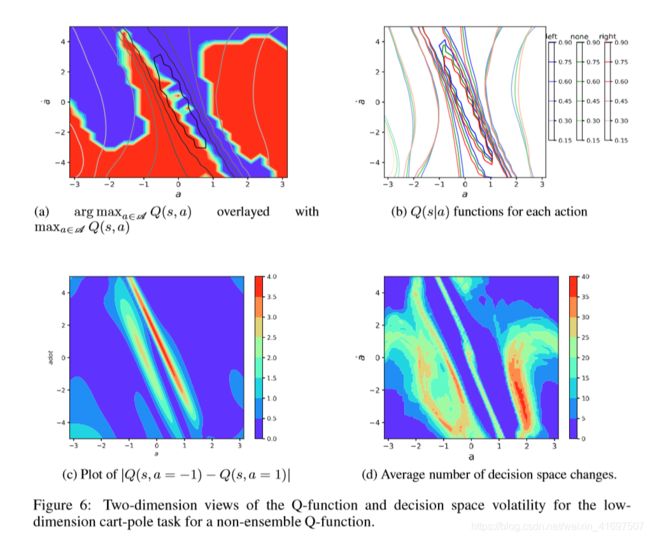
图7：尺寸为20的Q函数集合的低维车极任务的Q函数和决策空间波动率的二维视图。

可以针对每个离散动作绘制Q函数，如图6b所示。 在这里，我们看到跨越状态位置的Q函数存在相当大的差异，但是Q值仅在动作之间略微移位。

这导致Q函数的最陡区域中Q（s，a = -1）-Q（s，a = 1）的较大差异，但是状态空间区域中的相对小的差异具有较少的显着浮雕。 这种关系在图6c中可见，其中具有最大变化率的Q函数区域在动作之间具有最大的Q函数差异。

人群合奏对决策空间有稳定作用。对于单个Q函数，大多数参数更新导致改进或维持成功导致目标状态的决策空间。然而，相当一部分更新的破坏性足以导致决策空间发生重大变化，从而导致遗忘。因此，整体成员决策的简单组合将更有可能避免对决策空间进行不稳定的变更。图7b示出了与图6d中的变化相比减小的大小NE = 20的集合的动作变化的数量。

这种改进的稳定性来自于基于多数投票的决策空间变化的相对大的障碍。在图7a中示出了大小为20的十个集合的平均大多数大小。与通过参数更新所采用的噪声路径经常克服的小Q差异不同，大多数尺寸不是那么容易克服的。

7CONCLUSIONS AND FUTURE WORK

We have presented a simple ensemble approach to Q-learning which confronts the most common complaints about RL: that training takes too long and that training is unstable. The crowd ensemble approach to Q-learning can be used in tandem with other approaches including the most recent advances in the field. Instead of multiplying the number of interactions with the environment, as in recent, high-profile work, it increases the computational requirements but reduces the number of required interactions with the environment. Furthermore, each member of the crowd ensemble can be trained in parallel allowing for a negligible increase in wall-clock time. Our experiments demonstrate that the approach improves performance by reducing decision space volatility resulting in improved mean reward, a near elimination of catastrophic forgetting, an increase in the speed and reliability of learning, and an improvement in the quality of the solutions.

Our results regarding shared convolutional layers point to the potential for a dramatic speed-up in training for domains with high-dimension inputs. In this instance the instability of Q-learning worked to our advantage by providing the shared layers with a combined gradient which leads to more direct path toward high-quality features.

An important item of remaining work is a comparison of the crowd ensemble against more tradi-tional ensemble methods such as mixtures of experts which have not received widespread adoption in the RL literature. An important limitation of the crowd ensemble approach to Q-learning is that the ability of the ensemble is limited by the ability of the ensemble members. Mixture of experts style ensembles are designed specifically to not have this problem.
我们提出了一种简单的Q-learning集合方法，它面临着关于RL的最常见的抱怨：训练时间太长而且训练不稳定。 Q-learning的人群集合方法可以与其他方法一起使用，包括该领域的最新进展。与最近的高调工作相比，它不是将与环境的交互次数相乘，而是增加了计算要求，但减少了与环境所需的交互次数。此外，人群集合中的每个成员可以并行训练，从而允许壁钟时间的可忽略的增加。我们的实验表明，该方法通过减少决策空间波动性来提高绩效，从而提高平均回报率，几乎消除了灾难性遗忘，提高了学习的速度和可靠性，并提高了解决方案的质量。

我们关于共享卷积层的结果表明，对于具有高维输入的域，培训可能会大幅加速。在这种情况下，Q学习的不稳定性通过为共享层提供组合梯度来实现我们的优势，这导致更直接的路径朝向高质量特征。

剩下的工作的一个重要项目是将人群集合与更传统的集合方法（例如在RL文献中未被广泛采用的专家混合）进行比较。人群集成方法对Q学习的一个重要限制是整体的能力受到整体成员能力的限制。专家风格合奏的混合物专门设计为没有这个问题。

REFERENCES

A. Agostini and E. Celaya. A competitive strategy for function approximation in q-learning. In 2011 International Joint Conference on Artificial Intelligence, pp. 1146–1151, 2011.

Charles W Anderson, Minwoo Lee, and Daniel L Elliott. Faster reinforcement learning after pre-training deep networks to predict state dynamics. In International Joint Conference on Neural Networks (IJCNN), pp. 1–7. IEEE, 2015.

Leo Breiman. Bagging predictors. Machine learning, 24(2):123–140, 1996.

Kenji Doya and Kazuyuki Samejima. Multiple model-based reinforcement learning. Neural Com-putation, 14:1347–1369, 2002.

Ganger M. Hu W. Duryea, E. Exploring deep reinforcement learning with multi q-learning. Intelli-gent Control and Automation, (7):129–144, 2016.

Stefan Faußer and Friedhelm Schwenker. Neural network ensembles in reinforcement learning.
Neural Processing Letters, 41(1):55–69, 2015.

Francis Galton. Vox populi. Nature, 75:450–451, March 1907.

A. Hans and S. Udluft. Ensembles of neural networks for robust reinforcement learning. In Ninth International Conference on Machine Learning and Applications (ICMLA), pp. 401–406, Dec 2010. doi: 10.1109/ICMLA.2010.66.

Hado V. Hasselt. Double q-learning. In J. D. Lafferty, C. K. I. Williams,
J. Shawe-Taylor, R. S. Zemel, and A. Culotta (eds.), Advances in Neural Informa-
tion Processing Systems 23, pp. 2613–2621. Curran Associates, Inc., 2010. URL
http://papers.nips.cc/paper/3964-double-q-learning.pdf.

Reid Hastie and Tatsuya Kameda. The robust beauty of majority rules in group decisions. Psycho-logical review, 112(2):494, 2005.

Robert A Jacobs, Michael I Jordan, Steven J Nowlan, and Geoffrey E Hinton. Adaptive mixtures of local experts. Neural Computation, 3(1):79–87, 1991.

Diederik P. Kingma and Jimmy Ba. Adam: A method for stochastic optimization. In Proceedings of the International Conference on Learning Representations, 2015. URL http://arxiv.org/abs/1412.6980.

Matthew Lai. Giraffe: Using deep reinforcement learning to play chess. Master’s thesis, Imperial College London, 2015.

Richard P. Larrick and Jack B. Soll. Intuitions about combining opinions: Misappreciation of the averaging principle. Management Science, 52(1):111–127, 2006. ISSN 00251909, 15265501. URL http://www.jstor.org/stable/20110487.

Timothy P. Lillicrap, Jonathan J. Hunt, Alexander Pritzel, Nicolas Heess, Tom Erez, Yuval Tassa, David Silver, and Daan Wierstra. Continuous control with deep reinforcement learn-ing. In Proceedings of the International Conference on Learning Representations, 2016. URL http://arxiv.org/abs/1509.02971.

Volodymyr Mnih, Koray Kavukcuoglu, David Silver, Andrei A Rusu, Joel Veness, Marc G Belle-mare, Alex Graves, Martin Riedmiller, Andreas K Fidjeland, Georg Ostrovski, et al. Human-level control through deep reinforcement learning. Nature, 518(7540):529–533, 2015.

Volodymyr Mnih, Adria Puigdomenech Badia, Mehdi Mirza, Alex Graves, Timothy Lillicrap, Tim Harley, David Silver, and Koray Kavukcuoglu. Asynchronous methods for deep reinforcement learning. In International Conference on Machine Learning, pp. 1928–1937, 2016.

Martin Møller. A scaled conjugate gradient algorithm for fast super-
vised learning. Neural Networks, 6(4):525 – 533, 1993. ISSN 0893-
6080. doi: http://dx.doi.org/10.1016/S0893-6080(05)80056-5. URL
http://www.sciencedirect.com/science/article/pii/S0893608005800565.

Srinivasan Praveen Blackwell Sam Alcicek Cagdas Fearon Rory Maria Alessandro De Panneershel-vam Vedavyas Suleyman Mustafa Beattie Charles Petersen Stig Legg Shane Mnih Volodymyr Kavukcuoglu Koray Nair, Arun and David Silver. Massively parallel methods for deep rein-forcement learning. In International Conference on Machine Learning Deep Learning Workshop, 2015.

Tom Schaul, John Quan, Ioannis Antonoglou, and David Silver. Prioritized experience replay. In Proceedings of the International Conference on Learning Representations, 2016. URL http://arxiv.org/abs/1511.05952.

David Silver, Aja Huang, Christopher J. Maddison, Arthur Guez, Laurent Sifre, George van den Driessche, Julian Schrittwieser, Ioannis Antonoglou, Veda Panneershelvam, Marc Lanctot, Sander Dieleman, Dominik Grewe, John Nham, Nal Kalchbrenner, Ilya Sutskever, Timothy Lillicrap, Madeleine Leach, Koray Kavukcuoglu, Thore Graepel, and Demis Hassabis. Mastering the game of go with deep neural networks and tree search. Nature, 529:484–503, 2016. URL
http://www.nature.com/nature/journal/v529/n7587/full/nature16961.html.

David Surowiecki. The Wisdom of Crowds. Anchor Books, 2005.

Richard S. Sutton and Andrew G. Barto. Reinforcement Learning: An Introduction. MIT Press, 1998.

Open AI team. Openai gym. http://gym.openai.com/, 2016.

Jack L Treynor. Market efficiency and the bean jar experiment. Financial Analysts Journal, 43(3):
50–53, 1987.

Hado van Hasselt, Arthur Guez, and David Silver. Deep reinforcement learning with

double q-learning. Computing Research Repository, abs/1509.06461, 2015. URL http://arxiv.org/abs/1509.06461.

8APPENDIX

8.1 PSEUDO CODE ALGORITHM OF CROWD ENSEMBLE Q-LEARNING

An implementation of a crowd ensemble is shown in Algorithm 1. Specifically, this algorithm describes the steps used to train an ensemble of Q-functions to solve the low-dimension cart-pole task.

Lines 13 and 14 are the action voting and action selection steps. Lines 22–27 are repeated for each ensemble member meaning each ensemble member draws a unique set of training sequences to replay during training. Lines 24 and 25 are computations of the member-specific Q-function target values and error function for use during parameter updates.
算法1中示出了人群集合的实现。具体地，该算法描述了用于训练Q函数集合以解决低维度极点任务的步骤。

第13和14行是动作投票和动作选择步骤。 对于每个集合成员重复行22-27，意味着每个集合成员绘制一组唯一的训练序列以在训练期间重放。 第24和25行是在参数更新期间使用的成员特定的Q函数目标值和误差函数的计算。

8.2 DECISION SURFACES CHANGES IN FREQUENTLY VISITED STATE SPACES

Here we provide frames from two movies showing decision space volatility in state spaces visited for a typical solution to the cart-pole task. Surfaces changes across 20 non-ensemble Q-learners once each had solved the task and continuing until training stopped. The figure shows the fraction of those parameter updates which resulted in a decision space change at that state location. Here we see that an agent must pass through several regions of high volatility on its way to the goal. Once the goal is reached, however, it is safely located between two relatively unchanging regions. These figures show that, in the cart-pole swing-up task, the greatest cause of catastrophic forgetting where the agent appears to have forgotten much of what it has learned is a result of volatility in the regions of the state space that must be visited on the way to the goal.

Figure 9 shows the same states as Figure 8 but the decision space changes are computed from an ensemble of size NE = 20. The plots are scaled to keep the colors consistent between figures. In fact, the maximum fraction of time steps that a particular location in state space changes its selected action is nearly identical for the NE = 20 and NE = 1 case: just over 47% of the parameter updates.

The difference in state space volatility is striking! The ensemble has not removed volatility but it has mitigated it considerably. Furthermore, the regions of Figure 9 which have the most instability are the regions where it matters least: namely the decision surface boundary in and around the goal region which is surrounded by regions of low decision space volatility. The other regions of high decision space volatility for the ensemble is when the pole is pointed downward with little angular velocity where the action decision had little impact.
在这里，我们提供了两部电影中的帧，显示了所访问的状态空间中的决策空间波动，这是典型的推车极点任务解决方案。一旦每个人都解决了任务并持续到训练停止，表面会在20个非整体Q学习者中发生变化。该图显示了那些参数更新的分数，这些更新导致该状态位置的决策空间变化。在这里，我们看到代理商必须在通往目标的途中经过几个高波动性区域。然而，一旦达到目标，它就安全地位于两个相对不变的区域之间。这些数字表明，在推车极摆动任务中，灾难遗忘的最大原因是，经纪人似乎已经忘记了所学的内容，这是因为必须访问的国家空间区域的波动在去目标的路上。

图9示出了与图8相同的状态，但是决策空间变化是从尺寸NE = 20的整体计算的。绘图被缩放以保持图之间的颜色一致。实际上，对于NE = 20和NE = 1的情况，状态空间中的特定位置改变其所选动作的时间步长的最大部分几乎相同：仅超过47％的参数更新。

状态空间波动的差异是惊人的！整体并未消除波动性，但它已大大减轻了波动性。此外，图9中具有最不稳定性的区域是最不重要的区域：即在目标区域内和周围的决策表面边界，其被低决策空间波动的区域包围。对于整体来说，高决策空间波动的其他区域是当极点向下指向角速度很小的情况时，行动决策几乎没有影响。

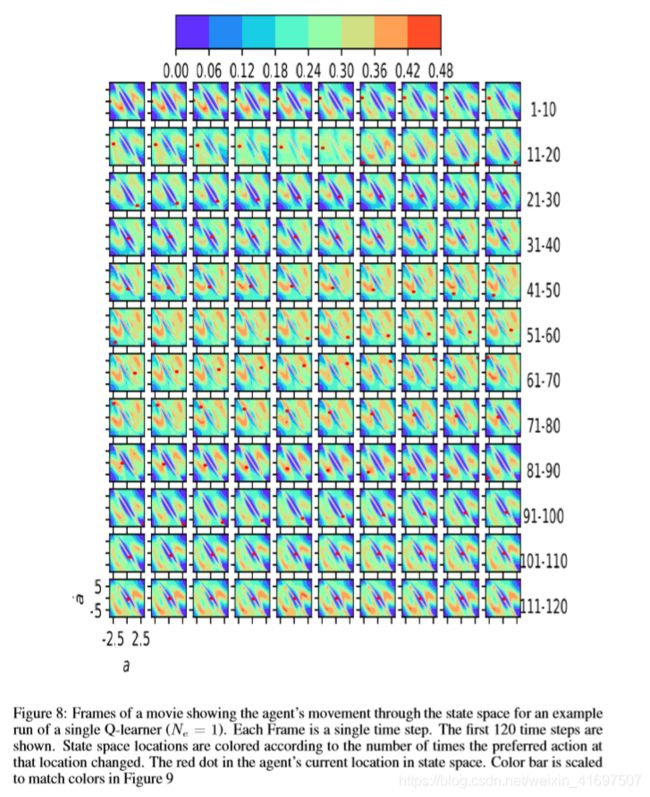
图8：电影的帧，显示代理通过状态空间的移动，用于单个Q-learner（NE = 1）的示例运行。 每个帧都是一个单一的时间步骤。 显示前120个时间步骤。 状态空间位置根据该位置的首选操作更改的次数着色。 代理程序在状态空间中的当前位置中的红点。 缩放颜色条以匹配图9中的颜色

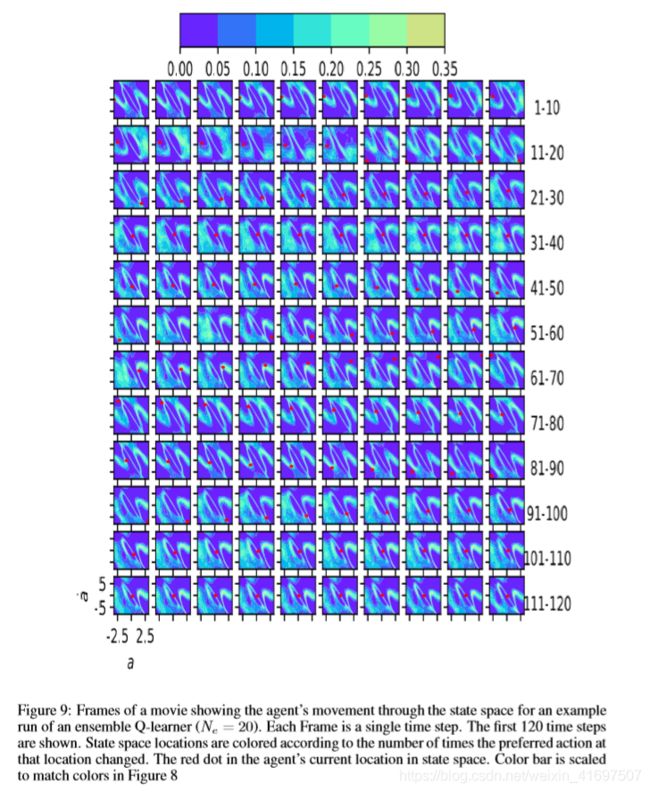
图9：电影的帧，显示代理通过状态空间的移动，用于集合Q学习器（NE = 20）的示例运行。 每个帧都是一个单一的时间步骤。 显示前120个时间步骤。 状态空间位置根据该位置的首选操作更改的次数着色。 代理程序在状态空间中的当前位置中的红点。 缩放颜色条以匹配图8中的颜色

8.3 CROWD ENSEMBLE DQN ADDITIONAL INFORMATION

图10：具有两个卷积层和两个完全连接层以及三个动作输出的深度Q学习网络示例。 示出了每个卷积层的两个示例输入帧和两个示例特征。 输入帧和后续功能是在培训期间从我们的DQN代理捕获的。

图10显示了两个特征的输出，每个特征来自两个输入帧计算的两个卷积层。 在这些框架中，杆子顺时针旋转。 特征一似乎突出了推车和杆的方向，在这个例子中都是向右的。 第一层特征之一的亮白色像素似乎是推车的前缘和指示方向的杆。 第一层的特征20可以编码相反的信息。 第二层中的一个特征似乎编码杆的位置，而特征40可以编码推车的位置。