20200819:力扣202周周赛题解记录
力扣202周周赛题解记录
-
- 题目一:[存在连续三个奇数的数组](https://leetcode-cn.com/problems/three-consecutive-odds/)
- 代码实现
- 题目二:[使数组中所有元素相等的最小操作数](https://leetcode-cn.com/problems/minimum-operations-to-make-array-equal/)
- 解题思路与代码实现
- 题目三:[两球之间的磁力](https://leetcode-cn.com/problems/magnetic-force-between-two-balls/)
- 解题思路与代码实现
- 题目四:[吃掉 N 个橘子的最少天数](https://leetcode-cn.com/problems/minimum-number-of-days-to-eat-n-oranges/)
- 解题思路与代码实现
题目一:存在连续三个奇数的数组
给你一个整数数组 arr,请你判断数组中是否存在连续三个元素都是奇数的情况:如果存在,请返回 true ;否则,返回 false 。
代码实现
class Solution {
public boolean threeConsecutiveOdds(int[] arr) {
if (arr.length < 3) {
return false;
}
for (int i = 0; i < arr.length - 2; i++) {
if ((arr[i] % 2 == 1) && (arr[i+1] % 2 == 1) && (arr[i+2] % 2 == 1) ) {
return true;
}
}
return false;
}
}
题目二:使数组中所有元素相等的最小操作数
存在一个长度为 n 的数组 arr ,其中 arr[i] = (2 * i) + 1 ( 0 <= i < n )。
一次操作中,你可以选出两个下标,记作 x 和 y ( 0 <= x, y < n )并使 arr[x] 减去 1 、arr[y] 加上 1 (即 arr[x] -=1 且 arr[y] += 1 )。最终的目标是使数组中的所有元素都 相等 。题目测试用例将会 保证 :在执行若干步操作后,数组中的所有元素最终可以全部相等。
给你一个整数 n,即数组的长度。请你返回使数组 arr 中所有元素相等所需的 最小操作数 。
解题思路与代码实现
本题思路也很简单,按照给定的n进行模拟即可,注意n的奇偶性导致的操作次数变化之间差1即可。注意书写
class Solution {
public int minOperations(int n) {
if (n == 1) {
return 0;
}
int ans = 0;
if (n % 2 == 0) {
for (int i = 1; i < n; i+=2) {
ans += i;
}
return ans;
} else {
for (int i = 1; i < n; i += 2) {
ans += (i + 1);
}
return ans;
}
}
}
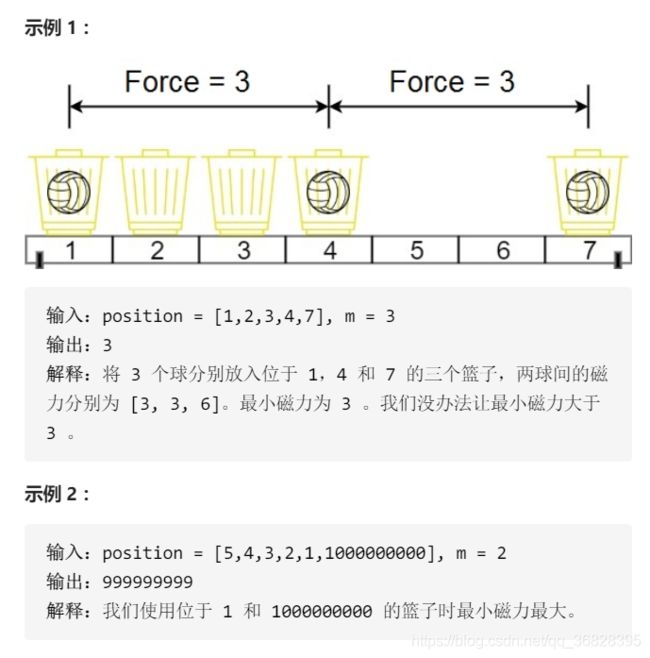
题目三:两球之间的磁力
在代号为 C-137 的地球上,Rick 发现如果他将两个球放在他新发明的篮子里,它们之间会形成特殊形式的磁力。Rick 有 n 个空的篮子,第 i 个篮子的位置在 position[i] ,Morty 想把 m 个球放到这些篮子里,使得任意两球间 最小磁力 最大。
已知两个球如果分别位于 x 和 y ,那么它们之间的磁力为 |x - y| 。
给你一个整数数组 position 和一个整数 m ,请你返回最大化的最小磁力。
解题思路与代码实现
首先根据示例1可以知晓position的最大和最小值确定要查找区间的两个边界,然后给的m个球确定该区间可以划分为m-1个区间,然后我们要找的使最下磁力最大在最理想的情况下为我们将这个区间平均分为m-1份,然后刚好对应的分界点处都有篮子,此时最简单,因此我们直接根据划分的距离来贪心可以放入的球的数量即可,若能放得下m个球,那么说明我们的距离还可以扩大,二分即可。
class Solution {
public int maxDistance(int[] position, int m) {
Arrays.sort(position);
int h = (position[position.length - 1] - position[0]) / (m - 1);
int l = 1;
int ans = 1;
while (l <= h) {
int mid = l + (h - l) / 2;
if (check(position, mid, m)) {
ans = mid;
l = mid + 1;
} else {
h = mid-1;
}
}
return ans;
}
boolean check(int[] position, int distance, int m) {
int cnt = 1;
int i = 0;
for (int j = 1; j < position.length; j++) {
if (position[j] - position[i] >= distance) {
i = j;
cnt++;
if (cnt >= m) return true;
}
}
return false;
}
}
题目四:吃掉 N 个橘子的最少天数
厨房里总共有 n 个橘子,你决定每一天选择如下方式之一吃这些橘子:
吃掉一个橘子。
如果剩余橘子数 n 能被 2 整除,那么你可以吃掉 n/2 个橘子。
如果剩余橘子数 n 能被 3 整除,那么你可以吃掉 2*(n/3) 个橘子。
每天你只能从以上 3 种方案中选择一种方案。
请你返回吃掉所有 n 个橘子的最少天数。
解题思路与代码实现
本题乍一看很简单,每次从后面两种情况来选择吃掉橘子的数量即可,很明显的动态规划题目,dp[i] 表示吃掉i个橘子需要的最少天数。则很明显的按照n能被2和3整除来划分情况即可,TLE代码如下:
class Solution {
public int minDays(int n) {
if (n == 1) return 1;
if (n == 2 || n == 3) return 2;
int[] dp = new int[n+1];
dp[0] = 0;
dp[1] = 1;
dp[2] = 2;
dp[3] = 2;
for (int i = 3; i < n + 1; i++) {
dp[i] = dp[i - 1] + 1;
if (i % 2 == 0) {
dp[i] = Math.min(dp[i],dp[i/2] + 1);
}
if (i % 3 == 0) {
dp[i] = Math.min(dp[i],dp[i/3] + 1);
}
}
return dp[n];
}
}
没错使用动态规划会超时,因为数据量的问题:1 <= n <= 2 * 10^9
那么我们得考虑其他的解法了,或者说对上述解法进行优化,参考大神的题解学到了新的离散化dp的思想,使用算法复杂度更低的哈希表来存储key和value,这样的话按照题目的含义,只需要遍历一遍即可完成dp。
class Solution {
HashMap<Integer,Integer> map = new HashMap<>();
public int minDays(int n) {
if (n <= 1) {
return n;
}
int min = Integer.MAX_VALUE;
if (map.containsKey(n)) {
return map.get(n);
}
min = Math.min(min,minDays(n / 2) + (n % 2));
min = Math.min(min,minDays(n / 3) + (n % 3));
// 需要额外1天吃到满足被2或者3整除,因此加1
min++;
map.put(n,min);
return min;
}
}