高斯列主元消去法、雅可比迭代法、高斯－塞德尔迭代法原理及使用（代码环境：matlab）

题目一：

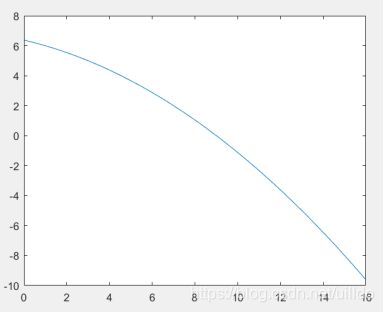
1.假设理想状态下的弹道轨迹满足抛物线方程y=a+bx+cx^2（注：真实状态下的轨迹并不是那样，一般发射后段的轨迹比较倾斜，这是因为后段受空气阻力的影响比较大。），已知弹道轨迹经过点（1，6）、（3，5）、（7，2），求此弹道轨迹抛物线方程。
要求: 采用列主元消去法求解，并画出此弹道轨迹抛物线图形。

高斯列主元消去法：

1.原理：

算法：

3.matlab代码：

A=[1,1,1;
   1,3,9;
   1,7,49];
b=[6,5,2];
n=length(b);%方程个数n
x=zeros(n,1);%未知向量
% m=zeros(1,3);
%-------------消去-----------
for k=1:n-1
    if A(k,k)==0;
        error('Error');
    end
    
     for j=2:n
         if A(k,1)

运行结果：

题目二：

2.对于第1题的弹道轨迹抛物线方程，根据已知的三个弹道轨迹经过点（1，6）、（3，5）、（7，2）建立的线性方程组，采用迭代法求解，得到此弹道轨迹抛物线方程。
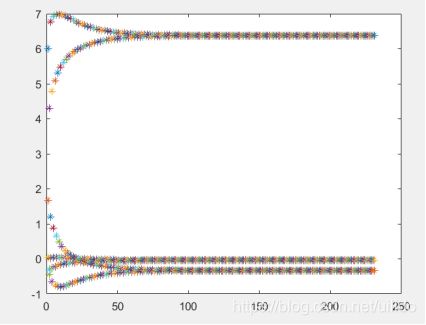
（1）采用雅可比迭代法求其近似解，并画出解随着迭代次数变化的趋势线（允许的最大迭代次数N，近似解的精度eps，由用户设定）。
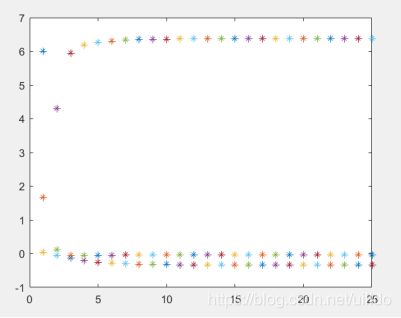
（2）采用高斯－塞德尔迭代法求其近似解，并画出解随着迭代次数变化的趋势线（允许的最大迭代次数N，近似解的精度eps，由用户设定）。

雅可比迭代法：

1.原理：

2.算法：
3.matlab代码：

A=[1,1,1;
   1,3,9;
   1,7,49];
b=[6,5,2];
n=length(b);%方程个数n
x=ones(n,1);%未知向量
x0=zeros(n,1);%未知向量
eps=10^(-5);
x0(1)=0;
N=2000;
k=0;
for i=1:n
    x(i)=x0(i);
    s=0;
    for j=1:n
        if j~=i
            s=s+A(i,j)*x0(j);
        end
    end
    x(i)=(b(i)-s)/A(i,i);
    
end
k=k+1;
plot(k,x(1),'*');
hold on;
plot(k,x(2),'*');
hold on;
plot(k,x(3),'*');
hold on;
 
while (abs(x(1)-x0(1))>eps || abs(x(2)-x0(2))>eps || abs(x(3)-x0(3))>eps)
    if k==N
        error('Error');
%            exit(0);
    end
    for i=1:n
        x0(i)=x(i);
    end 
    
    for i=1:n
        s=0;
        for j=1:n
            if j~=i
                s=s+A(i,j)*x0(j);
            end
        end
        x(i)=(b(i)-s)/A(i,i);
    end
    k=k+1;
    plot(k,x(1),'*');
    hold on;
    plot(k,x(2),'*');
    hold on;
    plot(k,x(3),'*');
    hold on;
end
% plot([1,2,3],x,'*');
plot(k,x(1),'*');
hold on;
plot(k,x(2),'*');
hold on;
plot(k,x(3),'*');
% hold on;

运算结果：

高斯－塞德尔迭代法

1.原理：

2.算法：

3.matlab代码：

A=[1,1,1;
   1,3,9;
   1,7,49];
b=[6,5,2];
n=length(b);%方程个数n
x=ones(n,1);%未知向量
x0=zeros(n,1);%未知向量
eps=10^(-5);
x0(1)=0;
N=2000;
k=0;
for i=1:n
    x(i)=x0(i);
    s=0;
    c=0;
    for j=1:i-1
            s=s+A(i,j)*x0(j);
    end
    
    for j=i+1:n
            c=c+A(i,j)*x0(j);
    end
    
    x(i)=(b(i)-s-c)/A(i,i);
    
end
k=k+1;
plot(k,x(1),'*');
hold on;
plot(k,x(2),'*');
hold on;
plot(k,x(3),'*');
hold on; 
while (abs(x(1)-x0(1))>eps || abs(x(2)-x0(2))>eps || abs(x(3)-x0(3))>eps)
    if k==N
        error('Error');
%            exit(0);
    end
    for i=1:n
        x0(i)=x(i);
    end 
    for i=1:n
        s=0;
        c=0;
        for j=1:i-1
            s=s+A(i,j)*x(j);
        end
        for j=i+1:n
            c=c+A(i,j)*x(j);
        end
        x(i)=(b(i)-s-c)/A(i,i);
    end
    k=k+1;
    plot(k,x(1),'*');
    hold on;
    plot(k,x(2),'*');
    hold on;
    plot(k,x(3),'*');
    hold on;
end
% plot([1,2,3],x,'*');
plot(k,x(1),'*');
hold on;
plot(k,x(2),'*');
hold on;
plot(k,x(3),'*');

运算结果：