最小二乘法曲线拟合(代码环境:matlab)
题目一:
1.用表1-1中的世界人口统计数值估计1980年的人口,求最佳最小二乘法数值估计:
表 1-1:
| 年 | 人口 |
|---|---|
| 1960 | 3 039 585 530 |
| 1970 | 3 707 475 887 |
| 1990 | 5 281 653 820 |
| 2000 | 6 079 603 571 |
(a) 直线;(b) 抛物线。它们都通过这些数据点,并求这些拟合的RMSE。在每一种情形下,估计1980年的人口。
实验原理:


(a) 直线估计1980年的人口结果及RMSE分析
matlab代码:
x=[1960 1970 1990 2000];
y=[3039585530 3707475887 5281653820 6079603571];
c=polyfit(x,y,1);
xi=1960:10:2000;
yi=polyval(c,xi)
plot(x,y,'*',xi,yi);
n=length(yi);
SE=0;
j=0;
for k=1:n
if k<=2
SE=SE+(yi(1,k)-y(1,k))*(yi(1,k)-y(1,k));
end
if k>3
j=k-1;
SE=SE+(yi(1,k)-y(1,j))*(yi(1,k)-y(1,j));
end
end
RMSE=sqrt(SE/4)
结果:


(b) 抛物线估计1980年的人口的结果及RMSE分析
matlab代码:
x=[1960 1970 1990 2000];
y=[3039585530 3707475887 5281653820 6079603571];
c=polyfit(x,y,2);
xi=1960:10:2000;
yi=polyval(c,xi)
plot(x,y,'*',xi,yi);
n=length(yi);
SE=0;
j=0;
for k=1:n
if k<=2
SE=SE+(yi(1,k)-y(1,k))*(yi(1,k)-y(1,k));
end
if k>3
j=k-1;
SE=SE+(yi(1,k)-y(1,j))*(yi(1,k)-y(1,j));
end
end
RMSE=sqrt(SE/4)
题目二:
世界石油产量以每天百万桶计,如表1-2所示,求最佳最小二乘法数值估计:
表1-2:
| 年 | 桶/天(×10^6) | 年 | 桶/天(×10^6) |
|---|---|---|---|
| 1994 | 67.052 | 1999 | 72.063 |
| 1995 | 68.008 | 2000 | 74.669 |
| 1996 | 69.803 | 2001 | 74.487 |
| 1997 | 72.024 | 2002 | 74.065 |
| 1998 | 73.400 | 2003 | 76.777 |
(a) 直线;(b) 抛物线;© 立方曲线。它们都通过10个数据点。并求这些拟合的RMSE。
(a) 直线估计世界石油产量2010年的生产水平,其估计结果及RMSE分析;
matlab代码:
x=[1994,1995,1996,1997,1998,1999,2000,2001,2002,2003];
y=[67052000 68008000 69803000 72024000 73400000 72063000 74669000 74487000 74065000 76777000];
c=polyfit(x,y,1);
xi=1994:1:2010;
yi=polyval(c,xi);
plot(x,y,'*',xi,yi);
RMSE=0;
SE=0;
for k=1:10
SE=SE+(yi(k)-y(k))*(yi(k)-y(k));
end
RMSE=sqrt(SE/10)
结果:


(b) 抛物线估计世界石油产量2010年的生产水平,其估计结果及RMSE分析;
matlab代码:
x=[1994,1995,1996,1997,1998,1999,2000,2001,2002,2003];
y=[67052000 68008000 69803000 72024000 73400000 72063000 74669000 74487000 74065000 76777000];
c=polyfit(x,y,2);
xi=1994:1:2010;
yi=polyval(c,xi);
plot(x,y,'*',xi,yi);
RMSE=0;
SE=0;
for k=1:10
SE=SE+(yi(k)-y(k))*(yi(k)-y(k));
end
RMSE=sqrt(SE/10)
结果:


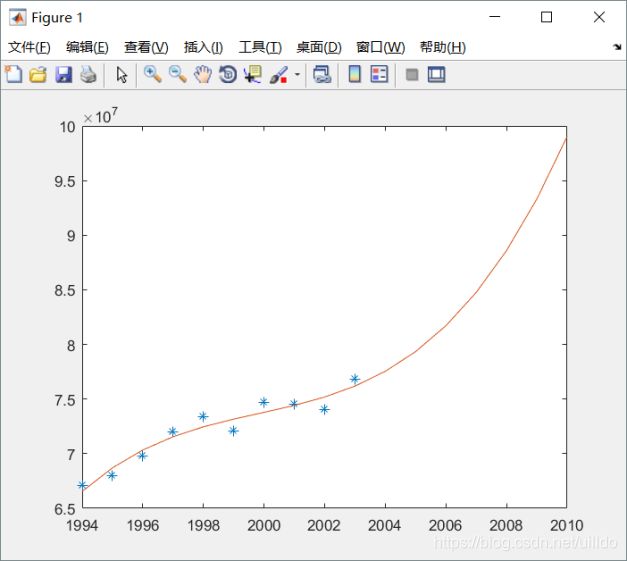
© 立方曲线估计世界石油产量2010年的生产水平,其估计结果及RMSE分析;
matlab代码:
x=[1994,1995,1996,1997,1998,1999,2000,2001,2002,2003];
y=[67052000 68008000 69803000 72024000 73400000 72063000 74669000 74487000 74065000 76777000];
c=polyfit(x,y,3);
xi=1994:1:2010;
yi=polyval(c,xi);
plot(x,y,'*',xi,yi);
RMSE=0;
SE=0;
for k=1:10
SE=SE+(yi(k)-y(k))*(yi(k)-y(k));
end
RMSE=sqrt(SE/10)