洛谷P3373 【模板】线段树2
在洛谷随便找了一题线段树的模板题,洛谷大牛的题解真是好评~
题目链接
大神题解
题目先给一个数组,然后给出一些操作
操作1: 格式:1 x y k 含义:将区间[x,y]内每个数乘上k
操作2: 格式:2 x y k 含义:将区间[x,y]内每个数加上k
操作3: 格式:3 x y 含义:输出区间[x,y]内每个数的和对P取模所得的结果
然后在询问时要输出区间和,要模p;
注意题目里k是要longlong所以区间和,lazy标签之类的都是longlong
先看一下线段树的基本知识;
现在如果给出了一个数组,如果要求一段连续区间和的话,那么容易想到可以使用树状数组,模板是这样的:链接
但是树状数组只能支持单点更新,那么如果题目要求区间更新的话,树状数组就不能胜任了,于是需要线段树;
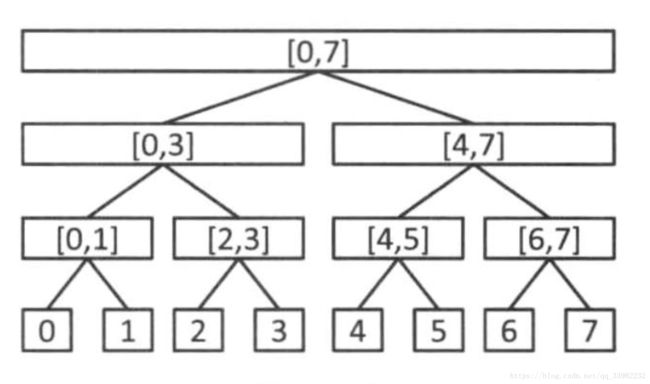
首先是基本的线段树,大概长这样,每个节点都维护自己节点的一些信息,比如sum值,那么比如叶子节点2,就存储了他自己的sum值就是a[2]的值,比如节点[0,3]节点就存储了0-3节点区间和。
那么它的实现方式是,建立好树之后,每次更新区间的时候,都更新叶子节点,然后自底向上的更新;
但是这样的实现效率比较低,所以我们对每个节点引入了lazy标签,比如现在如果要在0-2的区间上进行add k操作,那么我们就把0-1节点和2节点的lazy标签更新为k,同时把sum值更新,而暂时不用去更新0和1节点的sum值。
这样我们就不用每次更新的时候都去深入到叶子节点O(logn),可以攒足了很多add操作一起更新下去。
但是这题不仅有加法操作,还有乘法操作,所以应该需要两个lazy标签,一个标记加法,一个标记乘法;
思路分析用代码来表述吧,首先是节点,我们需要维护sum和lazy标签,注意都是longlong的:
struct node{
long long sum;
long long lazyadd,lazymul;
}A[maxx<<2];
然后是建树,建树的过程中把lazy标签要初始化,这里采用的是数组来表示树,因为线段树一定是平衡二叉树,所以基本上开数组空间也不会浪费很多,一般开max值的4倍肯定是够的;
void build(int u,int l,int r){//建树
A[u].lazymul=1;A[u].lazyadd=0;
if(l==r) A[u].sum=a[l];
else{
int mid=(l+r)/2;
build(2*u, l, mid);
build(2*u+1, mid+1, r);
A[u].sum=A[2*u].sum+A[2*u+1].sum;
}
A[u].sum%=p;
return ;
}然后是关键的pushdown操作:
void pushdown(int u, int l, int r){//把u节点的lazy标签向下分发
int mid=(l+r)/2;
//儿子的值=此刻儿子的值*爸爸的乘法lazytag+儿子的区间长度*爸爸的加法lazytag
A[u*2].sum=(A[u*2].sum*A[u].lazymul+A[u].lazyadd*(mid-l+1))%p;
A[u*2+1].sum=(A[u*2+1].sum*A[u].lazymul+A[u].lazyadd*(r-mid))%p;//r-(m+1)+1=r-m
//维护的lazytag
A[u*2].lazymul=(A[u*2].lazymul*A[u].lazymul)%p;
A[u*2+1].lazymul=(A[u*2+1].lazymul*A[u].lazymul)%p;
A[u*2].lazyadd=(A[u*2].lazyadd*A[u].lazymul+A[u].lazyadd)%p;
A[u*2+1].lazyadd=(A[u*2+1].lazyadd*A[u].lazymul+A[u].lazyadd)%p;
//把父节点的lazytag初始化
A[u].lazymul=1;
A[u].lazyadd=0;
return ;
}这里涉及到一个优先级的问题,当一个节点有两个标签时,优先更新哪个标签,刚开始我想的是对sum值先乘再加 和 先加再乘 的结果应该是不一样的,但是又考虑到,其实只要在做区间更新乘法的时候,把lazyadd标签的值也乘一下,这样就可以先乘再加了;但是如果想要先加后乘的话,比较复杂,就不去使用;在pushdown之后要记得把lazy标签初始化;
然后就是mul乘法和add加法和查询操作,就是要注意multiple的时候要把lazyadd标签也乘上k:
void mul(int u,int sl,int sr,int l,int r,long long k){//对节点u进行乘法更新,点u的左右范围是sl-sr,所需要更新的范围是l-r,乘k
if(l>sr || r=sr){
A[u].sum*=k;
A[u].lazymul*=k;
A[u].lazyadd*=k;
A[u].sum%=p;
A[u].lazymul%=p;
A[u].lazyadd%=p;
return ;
}
pushdown(u, sl, sr);
int mid=(sl+sr)/2;
mul(2*u, sl, mid, l, r, k);
mul(2*u+1, mid+1, sr, l, r, k);
A[u].sum=(A[2*u].sum+A[2*u+1].sum)%p;
return ;
}
void add(int u,int sl,int sr,int l,int r,long long k){//对节点u进行加法更新,点u的左右范围是sl-sr,所需要更新的范围是l-r,加k
if(l>sr || r=sr){
A[u].sum+=k*(sr-sl+1);
A[u].lazyadd+=k;
A[u].sum%=p;
A[u].lazyadd%=p;
return ;
}
pushdown(u, sl, sr);
int mid=(sl+sr)/2;
add(2*u, sl, mid, l, r, k);
add(2*u+1, mid+1, sr, l, r, k);
A[u].sum=(A[2*u].sum+A[2*u+1].sum)%p;
return ;
}
long long query(int u,int sl,int sr,int l,int r){//查询节点u,点u的范围是sl-sr,查询范围l-r内的总和sum
if(l>sr || r=sr) return A[u].sum;
pushdown(u, sl, sr);
int mid=(sl+sr)/2;
return (query(2*u, sl, mid, l, r)+query(2*u+1, mid+1, sr, l, r))%p;
} AC代码:
// luogu-judger-enable-o2
#define _CRT_SBCURE_NO_DEPRECATE
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
const int maxx = 1e5+6;
const int INF = 0x7fffffff;
int n,m,p;
int a[maxx];
struct node{
long long sum;
long long lazyadd,lazymul;
}A[maxx<<2];
void build(int u,int l,int r){//建树
A[u].lazymul=1;A[u].lazyadd=0;
if(l==r) A[u].sum=a[l];
else{
int mid=(l+r)/2;
build(2*u, l, mid);
build(2*u+1, mid+1, r);
A[u].sum=A[2*u].sum+A[2*u+1].sum;
}
A[u].sum%=p;
return ;
}
void pushdown(int u, int l, int r){//把u节点的lazy标签向下分发
int mid=(l+r)/2;
//儿子的值=此刻儿子的值*爸爸的乘法lazytag+儿子的区间长度*爸爸的加法lazytag
A[u*2].sum=(A[u*2].sum*A[u].lazymul+A[u].lazyadd*(mid-l+1))%p;
A[u*2+1].sum=(A[u*2+1].sum*A[u].lazymul+A[u].lazyadd*(r-mid))%p;//r-(m+1)+1=r-m
//维护的lazytag
A[u*2].lazymul=(A[u*2].lazymul*A[u].lazymul)%p;
A[u*2+1].lazymul=(A[u*2+1].lazymul*A[u].lazymul)%p;
A[u*2].lazyadd=(A[u*2].lazyadd*A[u].lazymul+A[u].lazyadd)%p;
A[u*2+1].lazyadd=(A[u*2+1].lazyadd*A[u].lazymul+A[u].lazyadd)%p;
//把父节点的lazytag初始化
A[u].lazymul=1;
A[u].lazyadd=0;
return ;
}
void mul(int u,int sl,int sr,int l,int r,long long k){//对节点u进行乘法更新,点u的左右范围是sl-sr,所需要更新的范围是l-r,乘k
if(l>sr || r=sr){
A[u].sum*=k;
A[u].lazymul*=k;
A[u].lazyadd*=k;
A[u].sum%=p;
A[u].lazymul%=p;
A[u].lazyadd%=p;;
return ;
}
pushdown(u, sl, sr);
int mid=(sl+sr)/2;
mul(2*u, sl, mid, l, r, k);
mul(2*u+1, mid+1, sr, l, r, k);
A[u].sum=(A[2*u].sum+A[2*u+1].sum)%p;
return ;
}
void add(int u,int sl,int sr,int l,int r,long long k){
if(l>sr || r=sr){
A[u].sum+=k*(sr-sl+1);
A[u].lazyadd+=k;
A[u].sum%=p;
A[u].lazyadd%=p;
return ;
}
pushdown(u, sl, sr);
int mid=(sl+sr)/2;
add(2*u, sl, mid, l, r, k);
add(2*u+1, mid+1, sr, l, r, k);
A[u].sum=(A[2*u].sum+A[2*u+1].sum)%p;
return ;
}
long long query(int u,int sl,int sr,int l,int r){
if(l>sr || r=sr) return A[u].sum;
pushdown(u, sl, sr);
int mid=(sl+sr)/2;
return (query(2*u, sl, mid, l, r)+query(2*u+1, mid+1, sr, l, r))%p;
}
int main (){
std::ios::sync_with_stdio(false);
cin>>n>>m>>p;
for(int i=1;i<=n;i++){
cin>>a[i];
}
build(1,1,n);
while(m--){
int x,y,z;
long long k;
cin>>z;
if(z==1){
cin>>x>>y>>k;
mul(1,1,n,x,y,k);
}
else if(z==2){
cin>>x>>y>>k;
add(1,1,n,x,y,k);
}
else{
cin>>x>>y;
cout< 错点:
1.pushdown中一定要注意先乘后加,而且在mul中要把lazyadd标签也乘k;
2.定义要开longlong
3.一定要在过程中取模,不能在输出的时候就取模,所幸 加法和乘法对于取模是自由的,所以无所谓;