POJ3321 树状数组(细节问题)
H - Apple Tree
There is an apple tree outside of kaka's house. Every autumn, a lot of apples will grow in the tree. Kaka likes apple very much, so he has been carefully nurturing the big apple tree.
The tree has N forks which are connected by branches. Kaka numbers the forks by 1 toN and the root is always numbered by 1. Apples will grow on the forks and two apple won't grow on the same fork. kaka wants to know how many apples are there in a sub-tree, for his study of the produce ability of the apple tree.
The trouble is that a new apple may grow on an empty fork some time and kaka may pick an apple from the tree for his dessert. Can you help kaka?
The first line contains an integer N (N ≤ 100,000) , which is the number of the forks in the tree.
The following N - 1 lines each contain two integers u and v, which means forku and forkv are connected by a branch.
The next line contains an integer M (M ≤ 100,000).
The following M lines each contain a message which is either
"C x" which means the existence of the apple on fork x has been changed. i.e. if there is an apple on the fork, then Kaka pick it; otherwise a new apple has grown on the empty fork.
or
"Q x" which means an inquiry for the number of apples in the sub-tree above the forkx, including the apple (if exists) on the fork x
Note the tree is full of apples at the beginning
3 1 2 1 3 3 Q 1 C 2 Q 1Sample Output
3 2
很迷的一道题啊,自己又是没有思路,还是借鉴别人的代码才做出来的,丢人啊!!!
这个题有一个很迷的地方,就是不能用vector v[maxn],要用vetor< vector
至少对于这道题来说,为此我还专门实验了下,在AC的程序里面分别加上不同规模的上述两种容器,第二种真
的是快一些,虽然对于有些初学者来说,第二种不知道是什么意思,但是通过这道题,我知道了
,以后要用数组+vector的 ,一定要改成vector+vector,避免超时,用起来也是一样的,
这一点一定要记住。至于比较快的原因,我个人猜测是取决去初始化吧,
大家有兴趣的可以自己查查。
再来讲讲思路吧,这道题一看就知道要用树状数组了,我也知道,但就是不知道怎么用,怎么转换,
然而对于大部分题,转换都非常关键,
很显然,第一步,我们需要把树状数组建起来,每个节点都是1,那就要调用n次add函数,但是,查询怎么办呢?
首先,我们要给这些点进行编号,
因为不能保证数据给的都是按顺序输入的,我们对节点,从上到下,从左到右编号,这就使我们想到了dfs,
就像走路一样, 有路就继续走,直到没路往回退,继续找到有路的地方,随之进行编号。
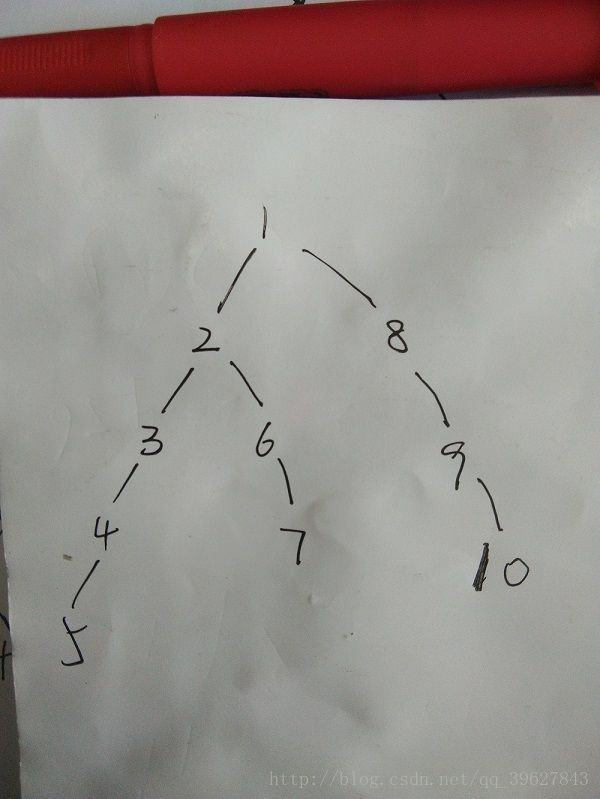
提示到这,大家可以在纸上画画了,看看有没有自己的思路,毕竟不能全部依靠别人。
然而,只进行一次编号是不能解决问题的。
就比如上个图,如果访问3的值,如果我们就直接getsum(3),完全是相反的,我们希望它把 3 4 5加起来,
所以getsum(5)-getsum(3-1)刚刚好。
即getsum(5)-getsum(2);
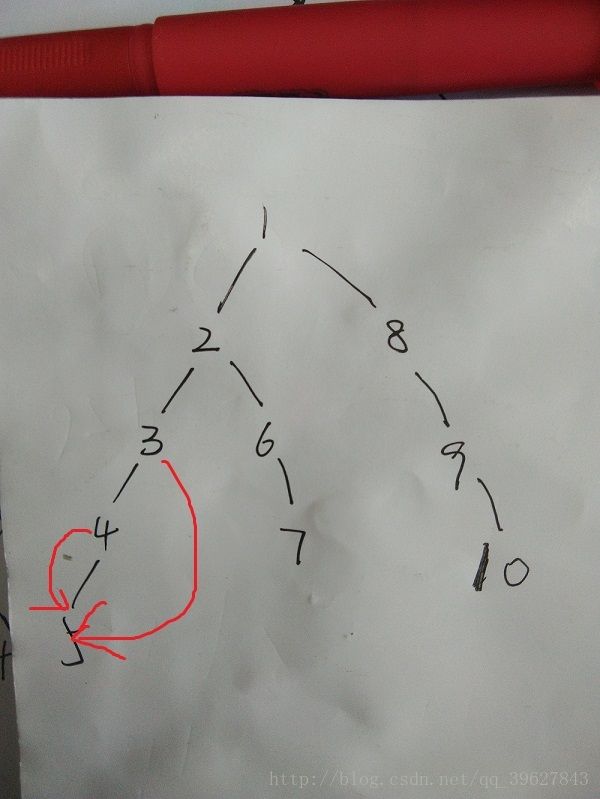
但是getsum(5)又怎么确定呢。这就要另外加一个索引了,就好比一个指针一样,让3这个地方有个指针指向5,如下图
有了这个“指针”我们就可以实现快速查询了,计算的原理是利用了前缀和。
再具体一点,每个节点保存两个索引,左值为本身,右值为其包含的所有后代中
最大的编号,就是上边说的那个类似指针的东西,那我们怎么实现呢?
递归递归递归, 哎,递归不会善用,真的是感觉差一大截,具体的看代码吧,我也感觉
我解释不清,最好是调试后把过程弄懂。
下面是代码
#include
using namespace std;
#include
#include
#include
#include
#include