并查集+例题
并查集的功能:
1:非常快的检查两个元素是否属于一个集合。
2:两个元素各自所在的集合,请你把它合并在一起。
并查集的基本组成部分(所用到的数据结构):
并查集有三个函数(也可以是两个)
一:find函数:寻找某个节点所在集合的头节点。
二:union函数:合并两个节点所在的集合。
三:issameset函数:判断两个节点是否属于一个集合。
所用到的数据结构:
数组:定义一个pre数组,pre[i]代表i节点的父节点,定义一个size数组,size[i]代表i节点所在的集合的元素的个数
map:定义一个fathermap,fathermap的key代表节点,value代表key节点的父节点,定义一个sizemap,sizemap的key也代表节点,sizemap的value代表key节点所在集合的节点个数
并查集压缩路径操作:
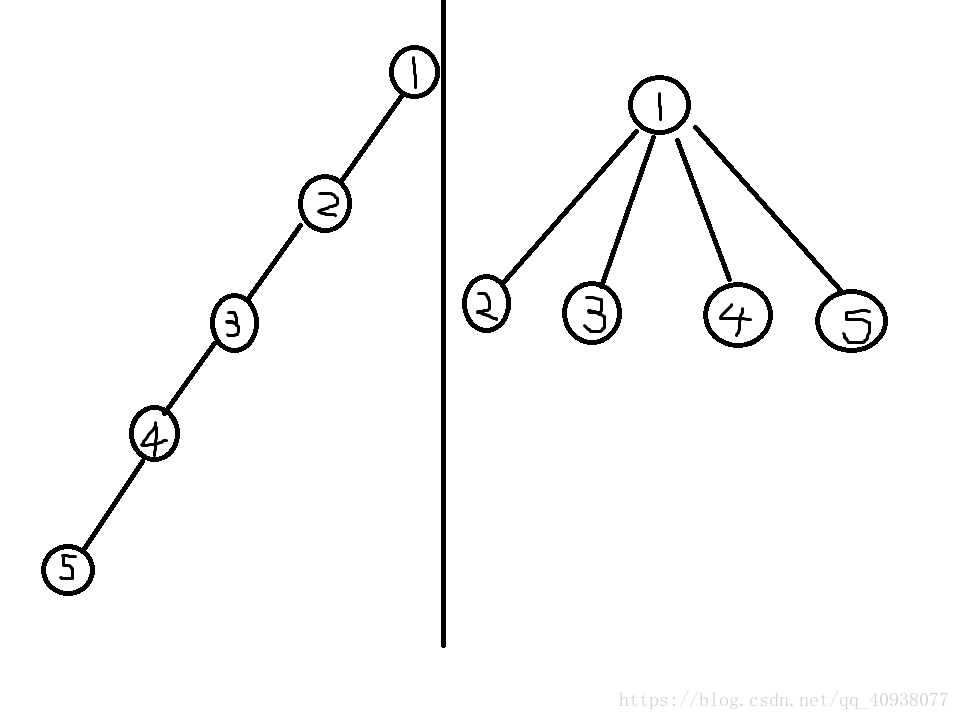
压缩路径:直接看图:
这就是路径压缩。
为什么要进行路径压缩呢?
当我们要查询4号节点和5号节点是否在一个集合中时,如果不进行路径压缩,那么就是上面的左图,从4号顶点一直走到1号顶点,从5号顶点一直走到1号顶点,很浪费时间。如果进行了路径压缩,那么就是上面的右图,从4号顶点走到1号顶点很方便,从5号顶点走到1号顶点也很方便。这就是并查集为什么能够很快的检查出两个元素是否属于一个集合的原因之一。
并查集的实现:
代码如下:
#include
#define MAXN 9999
using namespace std;
int a[MAXN];//用户提供的数据,必须一次性全部提供完
int n;//用户提供数据的个数
class unionfindset
{
private:
map < int,int >fathermap;//fathermap代表i节点(前面的int)的父亲节点(后面的int)
map < int,int >sizemap;//sizemap代表i节点(前面的int)所属的集合的大小(后面的int)
int findhead(int head)//寻找head节点所在集合的头节点,并压缩路径
{
int z=fathermap.find(head);//head节点的父亲节点(不一定是所在集合的头节点)
if(z==head)//找到了该集合的头节点
return head;
int father=findhead(z);//这个father变量始终是集合的头节点,不能变
fathermap[head]=father;//压缩路径
return father;//返回这个father,这样保证了father不会改变
}
public:
unionfindset()//构造函数,对两个map赋初值
{
for(int i=1;i<=n;i++)
{
fathermap[a[i]]=a[i];//我们设定刚开始有n个集合,每个集合的头节点都是自己本身
sizemap[a[i]]=1;//大小为1
}
}
bool issameset(int a,int b)//判断节点a和节点b是否属于同一个集合
{
return findhead(a)==findhead(b);
}
void uniona(int a,int b)//合并节点a和节点b
{
int heada=findhead(a);//找到a所在集合的头节点
int headb=findhead(b);//找到b所在集合的头节点
if(heada==headb)//如果相等,直接返回
return ;
int sizea=sizemap.find(heada);//获得a节点所在集合的大小
int sizeb=sizemap.find(headb);//获得b节点所在集合的大小
if(sizea>=sizeb)//我们规定,小集合合并到大集合当中去
{
fathermap[headb]=heada;//将b所在集合的头节点的父节点设置为a所在集合的头节点
sizemap[heada]=sizea+sizeb;//集合大小也更新
}
else
{
fathermap[heada]=headb;//同上,只不过是换了换
sizemap[headb]=sizea+sizeb;
}
return ;
}
};
这里我用的是map,也可以换成数组。
运用并查集的具体问题:
例题一:
题目链接:
https://www.luogu.org/problemnew/show/P1455#sub
代码:
#include
#include
#define MAXN 15000
using namespace std;
int money[MAXN],v[MAXN],money1[MAXN],v1[MAXN];
int pre[MAXN];
int sizea[MAXN];
int n,m,w,k=0;
int visited[MAXN];
int find(int x)
{
int z=pre[x];
if(z==x)
return x;
int father=find(z);
pre[x]=father;
return father;
}
void he(int a,int b)
{
int p=find(a);
int q=find(b);
if(p==q)
return ;
int asize=sizea[p];
int bsize=sizea[q];
if(asize>=bsize)
{
pre[q]=p;
sizea[p]=asize+bsize;
money[p]+=money[q];
v[p]+=v[q];
}
else
{
pre[p]=q;
sizea[q]=asize+bsize;
money[q]+=money[p];
v[q]+=v[p];
}
}
int main()
{
cin>>n>>m>>w;
for(int i=1;i<=n;i++)
cin>>money[i]>>v[i];
for(int i=1;i<=n;i++)
{
pre[i]=i;
sizea[i]=1;
}
for(int i=1;i<=m;i++)
{
int a,b;
cin>>a>>b;
he(a,b);
}
for(int i=1;i<=n;i++)
{
if(find(i)==i)
{
k++;
money1[k]=money[i];
v1[k]=v[i];
}
}
for(int i=1;i<=k;i++)
for(int j=w;j>=1;j--)
if(j-money1[i]>=0)
visited[j]=max(visited[j],visited[j-money1[i]]+v1[i]);
cout< 例题二:
题目链接:
http://acm.hdu.edu.cn/showproblem.php?pid=1232
思路:
裸的并查集的题目,将题目给定的数据通过并查集运行一遍,然后判断有多少个集合,答案就是集合数减一。
代码:
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define mod 1000000007
typedef long long ll;
using namespace std;
int n,m;
int x,y;
int father[1100];
int Size[1100];
void initialize()
{
for(int i=1;i<=n;i++)
{
father[i]=i;
Size[i]=1;
}
}
int findhead(int head)//寻找head节点的父亲节点,并且压缩路径
{
int z=father[head];
if(z==head)
return z;
int Father=findhead(z);
father[head]=Father;//路径压缩
return Father;
}
void uniona(int a,int b)//合并a节点和b节点到一个集合中去
{
int a_father=findhead(a);
int b_father=findhead(b);
if(a_father==b_father)
return ;
int a_size=Size[a_father];
int b_size=Size[b_father];
if(a_size>=b_size)//我们规定小的集合合并到大的集合中去
{
father[b_father]=a_father;
Size[a_father]=a_size+b_size;
}
else
{
father[a_father]=b_father;
Size[b_father]=a_size+b_size;
}
}
bool issameset(int a,int b)//判读a节点和b节点是否在一个集合中
{
return findhead(a)==findhead(b);
}
int main()
{
while(1)
{
cin>>n>>m;
if(n==0)
break ;
initialize();
for(int i=0;i>x>>y;
uniona(x,y);
}
int cnt=0;
for(int i=1;i<=n;i++)
if(father[i]==i)//如果有两个集合,那么就会有2个i值满足这个条件
cnt++;
cout<
例题三:
题目链接:
http://poj.org/problem?id=1611
题意:
一些学生被分组,0号学生感染病毒,跟他同一集合的也被感染,那么给出几个分组,问感染的人数
思路:
很简单的并查集的模板题,将给的数据进行一遍并查集操作,然后找出0号同学所在集合的同学个数,就是答案。
代码:
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define mod 1000000007
typedef long long ll;
using namespace std;
int n,m;
int father[30005];
int Size[30005];
void initialize()
{
for(int i=0;i=b_size)//我们规定小的集合合并到大的集合中去
{
father[b_father]=a_father;
Size[a_father]=a_size+b_size;
}
else
{
father[a_father]=b_father;
Size[b_father]=a_size+b_size;
}
}
int main()
{
while (~scanf("%d%d",&n,&m))
{
if(n==0&&m==0)
break ;
initialize();
for(int i=0;i
例题四:
题目链接:
http://codeforces.com/problemset/problem/277/A
题意:
https://www.cnblogs.com/nishikino-curtis/p/8798952.html
思路:
裸的并查集的题目,我们对题目给出语言进行并查集操作,找到连通块的数目,然后减一,加上不会任何一种语言的人数,就是答案,有一种特殊情况,就是所有人任何一种语言都不会,这种情况需要特判。
代码:
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define mod 1000000007
typedef long long ll;
using namespace std;
int n,m;
int father[1100];
int Size[1100];
bool visited[1100];
void initialize()
{
for(int i=1;i<=m;i++)
{
father[i]=i;
Size[i]=1;
}
}
int findhead(int head)
{
int z=father[head];
if(z==head)
return z;
int Father=findhead(z);
father[head]=Father;
return Father;
}
void uniona(int a,int b)
{
int a_father=findhead(a);
int b_father=findhead(b);
if(a_father==b_father)
return ;
int a_size=Size[a_father];
int b_size=Size[b_father];
if(a_size>=b_size)
{
father[b_father]=a_father;
Size[a_father]=a_size+b_size;
}
else
{
father[a_father]=b_father;
Size[b_father]=a_size+b_size;
}
}
int main()
{
while(cin>>n>>m)
{
memset(visited,false,sizeof(visited));
initialize();
int sum=0;
for(int i=0;i>k;
if(k==0)
{
sum++;
continue;
}
cin>>x;
visited[x]=true;
k--;
while(k--)
{
cin>>y;
visited[y]=true;
uniona(x,y);
}
}
int p1=0;//这个地方用p1加而不是直接用sum加的原因是有可能所有人都不会任何一种语言,此时并查集结构中不会有任何一个数,连通块的个数为零
for(int i=1;i<=m;i++)
if(visited[i]&&i==father[i])
p1++;
p1=max(0,p1-1);//这里就是判断并查集结构中没有连通块的情况,选择大的加到最后的结果中去
cout<