事件，时间与偏序关系

从牛顿力学进入爱因斯坦的相对论时空！

引言

这篇文章其实是对于《Time,Clocks,and the Ordering of Events in a Distributed System》这篇论文的论文笔记，但以这篇文章为契机，又想到了一些别的东西，所以挑选其中最为重要的概念，构成了这个题目。《Time,Clocks,and the Ordering of Events in a Distributed System》这篇论文的引用量是十分惊人的，这也从侧面展现了这篇文章对现代分布式领域所起到的极大的指导作用，Lamport大神以其及其敏锐的眼光看到分布式中时间的本质，在这篇文章中描述了分布式系统中事件与时间的关系，并把对于分布式中事件顺序的讨论与狭义相对论联系起来，并给出了如何在分布式系统中得到一个全序的关系，确实让人有一种茅塞顿开的感觉。说到分布式的时间，我想不少人都会不约而同的想到 Google Spanner 中的 TrueTime API，借助这个API实现全序关系的过程确实与文中Lamport给出的全序解决分布式互斥的过程有几分类似（当然物理时钟也避免了论文中所说外部事件产生的异常），可见八年前横空出世，领先业界的Spanner的核心早在几十年前就已经被Lamport及其深刻的思考过了，且这些思考现在看来也是如此深刻和富有远见。

这篇文章在首先描述了我对论文的理解，然后给出针对于论文中的想法对于全序关系的考虑。最后给出总结。

Happened Before与偏序

这篇文章的神奇之处在于其给出的想法是深入人心的，也就是看完文章以后在看待这个问题觉得一切都是那么自然，所以在看过文章之后所写下的这篇文章可能有些不客观。首先我们现实生活中是通过物理时钟来感受时间的流逝的，这其实可以简单的理解为一个特殊意义的中心授时点，比如格林威治时间；大家都遵守这个物理时钟，那么所有人事件的发生顺序就成了一个全序的关系，这也就成了我们老百姓眼中的时间，当然物理时钟是不可靠的，当然对于人类的生活来说显然造不成太大的影响（表慢30秒对于绝大多数人来说问题也不大）。但事实上我们没办法直接感受时间，我们能感受的只有事件的变化，那么在这种情况下我们唯一可以确定的就是因果关系，没有因果关系的事件我们都可以认为是并发的（在狭义相对论中，如果事件a是事件b的原因的话，那么在任何坐标系中，事件a都是b的原因，那么看到的都会是a先发生然后b发生，当然事件间存在因果关系也是有条件的），这也就是文中提出的Happened Before，既然事件之间只有Happened Before，那么我们就可以认为在某个系统中在不引人其他关系的情况下事件具有“偏序关系”。

一个分布式系统由一系列在空间上分离的多个进程组成，这些进程相互之间通过交换消息进行通信。在一个分布式系统中物理时钟是不可靠的，不同机器可能因为网络原因或者硬件原因导致时间并不一致，倘若我们想要在分布式系统中直接以物理时钟构建一个全序关系，因为上述原因显然是不可行的。此时我们引入Happened Before，也就是说如果 A Happened Before B，那么A一定发生在B之前，我们定义一个分布式系统由一系列进程组成，每一个进程包含一系列事件，那么显然在每一个进程内的（不考虑线程和协程）事件是一个全序关系，还有一种情况就是一个消息由事件A发出，由事件B接受（事件AB在分布式系统的不同的进程内），那么事件A Happened Before 事件B。我们定义 -> 为Happened Before，论文中对这个关系的定义如下：

1. 如果a和b是同一个进程中的事件，并且a在b前面发生，那么 a->b。
2. 如果a代表了某个进程的消息发送事件，b代表另一进程中针对这同一个消息的接收事件，那么a->b。
3. 如何 a->b且b->c，那么a->c。
4. 如果两个不同的事件a，b满足a(!->)b 且b(!->)a，我们就说a与b是并行的。

我们举个简单的例子：

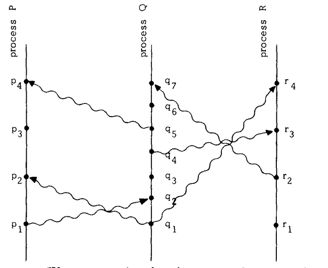
这幅图是论文中的图，我们以此举个例子，其中横轴代表了空间，纵轴代表了时间–坐标值越大时间越靠后。点代表了事件，垂直线代表了进 程，曲线代表了消息。我们很容易的看到在进程P中p1->p2，p2->p3，当扩展到多个进程的时候很显然的q1->p2，p1->q2，p1->r3，且其中p2与q2，p3与q3并发，因为它们之间没有任何的因果关系。

这样，我们就定义了一个偏序关系。

逻辑时钟

根据我们上面提到的两种分布式中可以实施的 Happened Before 关系， 我们可以引入一个逻辑时钟，首先我们定义Ci为进程i中为事件分配逻辑时钟号的函数，这就是一个单调递增的序列号，显然根据我们前文对于事件的讨论，我们可以得出：对于任意事件a，b：如果a->b，那么C(a) < C(b)，要满足这个条件，我们需要满足以下两个条件：

1. 如果a和b都是进程Pi里的事件，并且a在b之前，那么Ci(a)
2. 如果a是进程Pi里关于某消息的发送事件，b是另一进程Pj里关于该消息的接收事件，那么Ci(a)

这两个条件并不难实现，我们可以让进程遵循以下规则：

1. 每个进程Pi在任意连续的两个事件之间会增加Ci的值（单调递增的计数器即可）
2. 如果事件a代表了进程Pi发送消息m的事件，那么消息m包含的时间戳Tm=Ci(a)。(b)在收到消息m后，进程Pj会设置Cj的值使得它大于等于它的当前值并大于Tm.

这样我们可以得到一个实现偏序的逻辑时钟。

全序

我们前面一直在说偏序的问题，但是实际解决问题的时候我们大多需要全序关系，既然已经得到了偏序，那么我们如何优雅的得到全序呢？答案就是预定义一个进程之间的顺序，也就是在逻辑时钟相同的时候每一个节点使用相同的关系来对不同的事件进行排序，这样就得到了一个全序关系。我们来看看Lamport给出的定义：

1. 首先预定义一个进程间的任意全序关系“<”
2. 再定义一个新的关系“<=”，假设a是进程Pi中事件，b是进程Pj中的事件，那么当且 仅当满足如下条件之一时:
   1. Ci(a) < Cj(b)
   2. Ci(a) = Cj(b)，且Pi < Pj，那么我们就认为“a=>b”

这样我们就定义了一个全序关系，显然这个全序关系不是唯一的，因为“<”的定义不是唯一的。

论文中给出一个例子很有意思，这是一个去中心化互斥算法的雏形，并提出了状态机的概念，这篇论文不说别的，就这两个概念就足以流芳百世了。有意思的是状态机是一个这篇论文中很容易被忽略，但是却很重要的贡献，Lamport也在采访中也说到：

但是我碰到的人中，很少有人意识到该论文在说状态机相关的东西。看起来他们认为该论文是在讲分布式系统中事件的时序关系，或者是分布式互 斥算法。有些人还坚持声称该论文根本跟状态机无关，搞得我甚至重新回头读下这篇文章来确定我确实记得我写了什么。

我们来看看这个算法的细节和证明：

首先我们的问题是使用上述的全序关系设计一个算法解决一个分布式资源的互斥访问问题，这个算法需要满足以下三个条件：

1. 已经获得资源授权的进程，必须在资源分配给其他进程之前释放掉它；
2. 资源请求必须按照请求发生的顺序进行授权；
3. 如果获得锁的进程最终都都会释放锁的话，那么每一个 锁请求最终都会请求成功；

且我们需要有一些假设：

1. 对于任意的两个进程Pi和Pj， 它们之间传递的消息是按照发送顺序被接收到的；
2. 所有的消息最终都会被接收到；

当然这两个假设使用TCP（消息序号和确认机制）就可以实现了。

这个算法分为以下五个步骤：

1. 为请求该项资源，进程Pi发送一个Tm:Pi资源请求消息给其他所有进程，并将该消息放入自己的请求队列，在这里Tm代表了消息的时间戳;

2. 当进程Pj收到Tm:Pi资源请求消息后，将它放到自己的请求队列中，并发送一个带时间戳的确认消息给Pi。(注：如果Pj已经发送了一个时间戳大于Tm的消息，那就可以不发送);

3. 释放该项资源时，进程Pi从自己的消息队列中删除所有的Tm:Pi资源请求，同时给其他所有进程发送一个带有时间戳的Pi资源释放消息;

4. 当进程Pj收到Pi资源释放消息后，它就从自己的消息队列中删除所有的Tm:Pi资源请求（个人认为这里还需要进行回复）;

5. 当同时满足如下两个条件时，就将资源分配给进程Pi：

   a) 按照“=>”关系排序后，Tm:Pi资源请求排在它的请求队列的最前面;

   b) i已经从所有其他进程都收到了时间戳>Tm的消息(注：如果Pi=Tm的消息即可);

我们来证明这个算法一定满足三个条件：

• 对于条件1先假设不成立，也就是说B进程拿到资源以后，还有A进程持有资源，那么根据规则3，4，A进程并没有收到删除请求的消息，更没有回复了，根据假设，消息不会丢失，所以是根本没有发出删除消息的请求，A在队列中应该是最靠前的。而B进程拿到了资源，证明其满足规则5a，B应该是最靠前的，这就矛盾了，所以条件1成立。
• 规则5保证了条件2必然满足，我们需要证明规则5一定会被满足：首先规则1会向每一个进程发出消息，规则2保证了其他进程一定会回复一个时间晚于Tm的消息，而假设保证消息一定不会丢失，所以5.b满足。根据假设请求是按序分配的，规则3，4保证了使用完资源以后资源一定会被释放，也就是队列前的数据一直在被删除，后面的请求一定会被授权，规则5满足，所以条件2满足。
• 规则5一定会被满足，所以每一个请求最后都会被执行，所以条件3满足。

物理时钟

在这一部分把之前关于事件的讨论从系统事件扩展到系统事件与外部事件，我们会发现这可能产生一些非常令人匪夷所思的问题，比如：

假设某人在计算机A上产生了一个请求A，然后他打电话告诉住在另一个城市里的朋 友B，让它在计算机B上产生一个请求B。对于请求B来说很有可能会获得一个更小的时间戳然后被排在A前面

这个问题产生的原因是B的请求可能因为网络原因受到了无上界的延迟，显然打电话以后的这个请求属于外部事件，所以导致了这种奇怪的现象，有两种方法可以避免：

1. 将逻辑时间戳引入到外部事件，比如在用户产生请求A时得到系统内的逻辑时间戳，并将这个时间戳告诉用户B，显然，这会让用户很反感。
2. 在一个包含外部事件的系统内构造一个 happens before 关系，这个约束显然强于仅在分布式系统内构建 happens before，我们可以使用物理时钟来构建这个关系。

显然分布式中物理时钟是不可信的，但是Lamport在这篇文章中证明了如下两个条件：

1. 存在一个常数k，对于所有的i：| dCi(t)/dt - 1 | < k
2. 对于所有的i，j：| Ci(t)-Cj(t) | < e

有了这两个条件，我们可以像Spanner一样设计出一个类 TrueTime API，那么对于每一个C（i）我们都可以得到一个时间区间，保证真实物理时间在[ci - e，ci + e]之间，我们只需要在在每个操作的后面有一个像spanner一样的commit wait（操作效率时延与e挂钩），就可以保证利用物理时间来得到全局的全序关系了。

当然使用物理时间来达到全序关系实在不是一个简单的事情，哪怕到现在，根据[4]中的资料低误差的纯物理时钟也仅有Spanner一家而已，它依赖于特定硬件设备的思路，不适用于开源软件，所以很多已有的全局时钟基本都选择了混合逻辑时钟（Hybrid Logical Clock），与TSO（Timestamp Oracle），也有小众的比如巨衫的STP(SequoiaDB Time Protoco)。

对全序关系的思考

在分布式系统中没有人不对这个词不感到着迷，因为这意味着全局事件顺序是一致的，换句话说，我们可以把一个分布式系统当做一台庞大的机器来看待，这样我们就可以实现任意单机可以实现的功能，即实现任意分布式系统！Lamport本人也说到：

我很快就意识到该定义事件全序关系的算法可以用来实现任意的分布式系统。一个分布式系统可以描述为一个特殊的具有多个由网络互联的处理器的串行状态机。如果能够对输入请求进行全排序，就能够实现任何由 网络互联的处理器组成的状态机，因此也就可以实现任意的分布式系统

我们举两个例子来看一看，第一个例子就是分布式资源互斥问题，也就是文中提到的问题，也许换个说法更让人感到亲切，即分布式锁。分布式锁究其本质就是一个实现全序关系的问题，显然单机是很好实现这个问题的，我在另一篇文章《浅谈分布式锁：安全与性能的取舍之道》中简单的描述过分布式锁这个问题，但是当时我并没有意识到这其实就是一个全序的问题，当时描述的方案到现在看来不过时单点授时的不同手段而已，因为自身实现的原因而导致了因为性能和准确性而导致人们做出了不同的选择，但实质都是一个东西而已，现在看来当时的眼光还是太过浅显。我们在上文已经详细的描述了互斥算法的解决方案。我们再来看看其他全序关系的例子，我们可以利用这个特性完成一个一致性算法，既然已经是全序，那么其本身已经保证了一致性，那么如何解决fail-stop呢？我们可以使得全局对宕机以后成为主的节点序列得到一个全序关系，那么宕机以后所有节点发现后都会选择列表中的下一个作为主，这个列表小于等于节点总数。

当然上面的讨论没有考虑很多细节，比如论文中的分布式互斥算法基本没有可用性，因为无法容忍任何一个节点的失败。一致性算法还需要很多其他部分，比如集群变更，日志压缩等。

全序关系与无锁编程

对于分布式中全序关系的思考几乎使我立马想到了无锁编程（这里只基于C++进行讨论），我们来讨论一下对全序关系的思考可以使我们得到哪些启发。

在维基百科中对于分布式系统的定义是这样的：

分布式操作系统（Distributed operating system），是一个软件，它是许多独立的，网络连接的，通讯的，并且物理上分离的计算节点的集合。

我们暂且把这段定义简单的看做使用TCP通信的多个进程，如果我们此时忽略消息传输延迟与单个处理单元内部事件时间间隔相比差别明显的话，我们可以把一个进程中的多个线程当做是一个分布式系统中的多个计算节点，此时思路逐渐清晰起来，因为我们此时成了上帝，我们可以在这个系统内设置任意的 happens before 关系，因为线程间共用页表，我们有机会在汇编中加上额外的同步指令实现除了 Happened Before与偏序 这一节描述的两个偏序关系以外的其他关系。

我们举两个简单的例子，首先是C++内存序中的std::memory_order_release/std::memory_order_acquire，这其实就是在偏序那一节中描述的第二个关系，这相当于在两个线程之间建立了一个偏序关系，当然使用这两个内存序的变量也不会出现条件竞争。

第二个例子就是C++原子操作库的屏障，即std::atomic_thread_fence，还记得当时半年以前学这个的时候极其懵逼，现在就有了一种一览众山小的感觉了 ，这其实就是使得我们在两个线程毫不相关的基础上凭空给出了一个同步点，这两点之间 Happened Before ，且每个线程内的所有事件 Happened Before。

其实对于fence，在MIT 6.824中有一课的资料是go的内存模型，中文版中的一个例子就让我想到了fence，正好拿来解释一下上面的描述：

假设有两两个线程正在运行：

进程A：-- w0 – r1 – r2 ---- w3 ---- w4 ---- r5 -------->
进程B：-- w1 ----- w2 – r3 ---- r4 ---- w5 -------->

尽管w3实际发生时间早于r4，但是因为两者处于两个线程，没有任何的因果关系，我们认为这两个操作并发执行。我们假设并发写不会损坏数据，但是每次读可能读到不同的值。举个例子，r4可能读到w0，w2，w3，r5可能得到w1，w2，w5，w4的值，倘若我们在其中指定一个强制的因果关系，设“ | ”代表fence，如下：

进程A：-- w0 – r1 --…-- w3 -|----…-------|-- r5 ------>
进程B: — w1 — w2 ---- r3 —|- r4 – w5 --|------->

我们称第一组“ | ”为fence1，第二组为fence2，因为是 Happened Before，所以在指定fence之前会指定一组内存序，我们假设每一组fence有两个，分别称为A1和A2，各代表一个执行点，表示A1 Happened Before A2，我们假设“ -> ”代表Happened Before，因为fence1A->fence1B，fence1B->r4，w3->fence1A，所以r4就不可能读到w0了，但是w3和w2仍然是并发的。但是在fence2处就不一样了，因为fence1的缘故，如果我们设定 fence2B->fence2A，偏序具有传递的性质，且w3->w5，所以r5只能看到w5，如果设定fence2A->fence2B呢？此时r5和w5是并发的，那么r5可能看到w3或者w5。

总结

借用其他博主的一句话，这篇paper本对于现代分布式理论的意义不亚于狭义相对论之于现代物理学。可见这篇文章有多么的经典，Lamport对于分布式中时间的看法着实是一针见血，不仅仅是分布式，我觉得这个理念甚至可以用在并发编程或者其他我还没有涉足的知识点上，可见知识的本质都是相通的，实在是绝知此事要躬行啊。

感觉无锁编程相关的知识点都忘的差不多了，最近有时间的话再温习温习，毕竟很久以前就因为我找到的文章都太烂而想针对于C++的内存序写一篇文章，但是无奈理解不够作罢，现在感觉又站在了另一个角度看待内存序，实在是应该记录一下的，不管对于我后来温习还是初学C++无锁编程的同学都是很好的资料，最近太懒了，还是等闲了且不懒了再说吧。

参考：

1. 博文《读书笔记 - Time, Clocks and the Ordering of Events in a Distributed System》
2. 博文《Time,Clocks,and the Ordering of Events in a Distributed System 读书笔记及个人见解》
3. 博文《事件和时间：Time, Clocks, and the Ordering of Events in a Distributed System 读后感》
4. 课程《分布式数据库30讲》
5. 博文《浅谈分布式锁：安全与性能的取舍之道》
6. 维基《分布式操作系统》
7. 文档《Go 内存模型》