最短路径算法-Dijkstra
最短路径问题,我么一般也是在带权图中进行求解。即对于一个图来说,从一个点到另一个点我们要找到一个路径,这个路径上的总权值最小。一般我们在路径规划非常常见。
单源最短路径
我们在说带权图的最短路径的时候,我们从一个固定的点出发,一直走到图中任意一个目标顶点的路径。
带权图和无权图的最短路径求法有什么不同。 对于无权图的,我们只要边数越少,路径的总长度肯定越少,但是带权图就不一样了, 由于边上有权值,可能绕道走,多走几条边,路径会更短。比如,我们做飞机去某个城市,直接飞可能票价是比较高的,多次绕道转机,费用可能会更低。 如果我们把费用作为权值的话,多绕几次,总价格反而比直飞更加便宜。
Dijkstra 算法
Dijkstra不能处理负权边。这是前提。 就像我们使用二分搜索必须要让数据有序一样。 不过生活中的大量实际问题,不依赖于负权边。
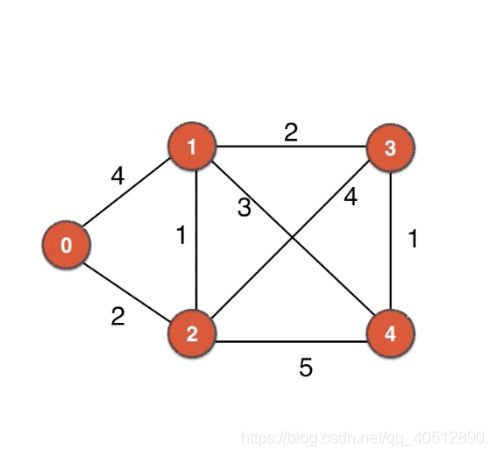
表示从源s到当前顶点的最短路径 初始是设置为 正无穷 (用#表示)我们还需要设置一个源比如0,我们通过0 可以直接到达顶点 1 和 顶点2 此时我们就可以更新dis数组了,顶点1 到源s的当前最短路径为4, 顶点2到源s的当前最短距离为2, 顶点3 和顶点4 由于无法直达,暂时无法更新。我们的0此时已经是最短路径上的点了。 我们用*号标识一下。0就是起点
dis 0 1 2 3 4
0* 4 2 # #
这个时候,我们在dis不是无穷,并且,还没有在最终路径上确认下来的点中,选择 dis值最小的一个点。就是顶点2 , 此时我们就可以说,从起点到2这个顶点的最短径长度就是2。 这是为什么呢? 我们凭什么就敢这么说呢? 这是因为,当前,我们选择的2 这个点的距离是从上一个最短路上的顶点直达过来的,如果你要证明还有更短的路可以到达这里,必然需要绕道。 但是,我们发现由于剩余其他未确认的点的dis 值都比2的dis值大,由于图中没有负权边,那么,从其他点再绕到2 这个点,只会让路径的长度更大。 因此,2这个点再最短路径上就确定下来了,起点 0 到 顶点2 的最短距离就是 2
dis 0 1 2 3 4
0* 4 2* # #
对于不是最小长度的那些顶点,我们还不能确定,因为可以通过当前确定的点,绕道过去,也许会让整个距离更短。
那么,我们新求出一个dis 2 的距离,下一步,我们就需要根据dis 2 这个距离,对还没有求出最终距离的顶点做一次更新。我们看一下,从2出发的相邻顶点,是不是可以做更新。
0--2--1 --> 长度为2+1 = 3 < 0--1 dis(1) =4
此时我们就可以更新dis(1) = 3
同样的道理,我们可以更新与2邻接顶点4,dis(4)为7 , 与2邻接的顶点 3 dis(3) 为 6
dis 0 1 2 3 4
0* 3 2* 6 7
那么,当前还没有确定最小距离的顶点还有 1 、3 、4 其中dis 值最小的是,顶点1,此时我们就可以肯定dis(1) = 3 这个值就是原点0 到顶点1 的最短路径长度
dis 0 1 2 3 4
0* 3* 2* 6 7
于是同样通过顶点1 , 我们需要更新 与顶点1邻接,并且还没有在最后的路径距离上确定下来的点。也就是顶点4 和顶点3
我们通过顶点1到达到顶点3 的距离为
dis(1) + weight(1-->3) = 3+2 = 5 而之前的dis(3)= 6 此时可以更新dis(3)=5
我们通过顶点1到达顶点4的距离为
dis(1)+weight(1--4)= 3+3 =6 而之前dis(4) = 7 此时可以更新dis(4) = 6
dis 0 1 2 3 4
0* 3* 2* 5 6
此时我们就可以确定 还没有确定的顶点中,顶点3的最短路径长度就是5
dis 0 1 2 3 4
0* 3* 2* 5* 6
此时我们在顶点3 开始更新它所有还没有确定的顶点 只剩下顶点4.
dis(3) + weight(3-->4) = 5+1 = 6 并不比dis(4)要更小,此时不需要更新
dis 0 1 2 3 4
0* 3* 2* 5* 6*
每一轮循环: 找到当前没有确定下来的最短路径的节点 , 确认这个顶点的最短路就是当前最短路的大小。
dis[b] = min(dis[b] , dis[a] + wight(a->b))
dis[c] = min(dis[c] , dis[a] + weight(a->c))
实现Dijkstar算法
import java.util.Arrays;
public class Dijkstra {
private WeightedGraph g;
private int s; // 原点s
private int[] dis;
private boolean[] visited; // 还没有确定下来的顶点为false
public Dijkstra(WeightedGraph g, int s) {
this.g = g;
g.validateVertex(s);
this.s = s;
dis = new int[g.V()];
visited = new boolean[g.V()];
Arrays.fill(dis, Integer.MAX_VALUE);
dis[s] = 0;
// 初始时,不能把visited[s] 设置为true 我们要找的第一个点就是s
// 算法的核心部分
while (true) {
// 第一件事: 找出当前还没有确定的顶点中 dis 最小的顶点 我们的第一个点及时原点
int curdis = Integer.MAX_VALUE, cur = -1;
for (int v = 0; v < g.V(); v++) {
if (!visited[v] && dis[v] < curdis) {
curdis = dis[v];
cur = v;
}
}
if (cur == -1) // 全部遍历完毕
break;
visited[cur] = true; // 第二件事 求出一个顶点
for (int w : g.adj(cur)) {
// 第三件事 更新邻接点
if (!visited[w]) {
if (dis[cur] + g.getWeight(cur, w) < dis[w])
dis[w] = dis[cur] + g.getWeight(cur, w);
}
}
}
}
public boolean isonnectedTo(int v) {
g.validateVertex(v);
return visited[v]; // 其实是判断连通性,如果是连通的,早晚会设置为true
}
public int disTo(int v) {
// 返回起点到顶点v的最短距离
g.validateVertex(v);
return dis[v];
}
public static void main(String[] args){
WeightedGraph g =new WeightedGraph( "g6.txt");
Dijkstra dijkstra = new Dijkstra(g ,0) ;
for(int v = 0 ;v<g.V() ;v++)
System.out.printf("%d " , dijkstra.disTo(v)) ;
}
}
整个算法的时间复杂度大致是 O (v ^2) 级别。
Dijkstra 算法的优化
我们的算法瓶颈在哪里? 就是在每次找当前未访问的dis 值最小的顶点。 就是找一个最小值,我们是不是可以用某些数据结构优化这里。 —答案是优先队列。
while (true) {
// 第一件事: 找出当前还没有确定的顶点中 dis 最小的顶点 我们的第一个点及时原点
int curdis = Integer.MAX_VALUE, cur = -1;
for (int v = 0; v < g.V(); v++) {
if (!visited[v] && dis[v] < curdis) {
curdis = dis[v];
cur = v;
}
}
if (cur == -1) // 全部遍历完毕
break;
visited[cur] = true; // 第二件事 求出一个顶点
for (int w : g.adj(cur)) {
// 第三件事 更新邻接点
if (!visited[w]) {
if (dis[cur] + g.getWeight(cur, w) < dis[w])
dis[w] = dis[cur] + g.getWeight(cur, w);
}
}
}
import java.util.Arrays;
import java.util.PriorityQueue;
public class Dijkstra2 {
private WeightedGraph g;
private int s; // 原点s
private int[] dis;
private boolean[] visited; // 还没有确定下来的顶点为false
private class Node implements Comparable<Node> {
public int v, dis;
public Node(int v, int dis) {
this.v = v;
this.dis = dis;
}
@Override
public int compareTo(Node node) {
return this.dis - node.dis;
}
}
public Dijkstra2(WeightedGraph g, int s) {
this.g = g;
g.validateVertex(s);
this.s = s;
dis = new int[g.V()];
visited = new boolean[g.V()];
Arrays.fill(dis, Integer.MAX_VALUE);
dis[s] = 0;
// 初始时,不能把visited[s] 设置为true 我们要找的第一个点就是s
// 核心算法
PriorityQueue<Node> pq = new PriorityQueue<Node>();
pq.add(new Node(s, 0));
while (!pq.isEmpty()) {
// 第一件事: 找出当前还没有确定的顶点中 dis 最小的顶点 我们的第一个点及时原点
int cur = pq.remove().v; //log 级别的复杂度
if (visited[cur]) continue; // 处理优先队列带来的副作用
visited[cur] = true; // 第二件事 求出一个顶点
for (int w : g.adj(cur)) {
// 第三件事 更新邻接点
if (!visited[w]) {
if (dis[cur] + g.getWeight(cur, w) < dis[w]) {
dis[w] = dis[cur] + g.getWeight(cur, w);
pq.add(new Node(w, dis[w]));
// 一个顶点可能存在多份 我们在优先队列中进行更新 这样的副作用是,我们后来在pq中取出顶点
// 这个顶点很可能之前已经被处理过了。
}
}
}
}
}
public boolean isonnectedTo(int v) {
g.validateVertex(v);
return visited[v]; // 其实是判断连通性,如果是连通的,早晚会设置为true
}
public int disTo(int v) {
// 返回起点到顶点v的最短距离
g.validateVertex(v);
return dis[v];
}
public static void main(String[] args) {
WeightedGraph g = new WeightedGraph("g6.txt");
Dijkstra2 dijkstra = new Dijkstra2(g, 0);
for (int v = 0; v < g.V(); v++)
System.out.printf("%d ", dijkstra.disTo(v));
}
}
最多情况下,优先队列最多存储 E 个元素也就是把每条边都放入了一份。 现在的时间复杂度是 O ( E * logE) 级别
更多Dijkstra 算法讨论
求解具体的最短路径。 用一个pre 数组,每一个顶点最终是从哪个来的。 最后我们从终点倒推回去就可以。 比较关键的是,这个pre 数组赋值发生在哪里。 实际上,这个赋值,发生在更新dis距离的时候。
pre [w] = cur
import java.util.ArrayList;
import java.util.Arrays;
import java.util.Collections;
import java.util.PriorityQueue;
public class Dijkstra2 {
private WeightedGraph g;
private int s; // 原点s
private int[] dis;
private boolean[] visited; // 还没有确定下来的顶点为false
private int[] pre;
private class Node implements Comparable<Node> {
public int v, dis;
public Node(int v, int dis) {
this.v = v;
this.dis = dis;
}
@Override
public int compareTo(Node node) {
return this.dis - node.dis;
}
}
public Dijkstra2(WeightedGraph g, int s) {
this.g = g;
g.validateVertex(s);
this.s = s;
dis = new int[g.V()];
visited = new boolean[g.V()];
pre = new int[g.V()];
Arrays.fill(pre, -1);
Arrays.fill(dis, Integer.MAX_VALUE);
dis[s] = 0;
pre[s] = s; // 源点的上一个顶点是自己
// 初始时,不能把visited[s] 设置为true 我们要找的第一个点就是s
PriorityQueue<Node> pq = new PriorityQueue<Node>();
pq.add(new Node(s, 0));
while (!pq.isEmpty()) {
// 第一件事: 找出当前还没有确定的顶点中 dis 最小的顶点 我们的第一个点及时原点
int cur = pq.remove().v; //log 级别的复杂度
if (visited[cur]) continue; // 处理优先队列带来的副作用
visited[cur] = true; // 第二件事 求出一个顶点
for (int w : g.adj(cur)) {
// 第三件事 更新邻接点
if (!visited[w]) {
if (dis[cur] + g.getWeight(cur, w) < dis[w]) {
dis[w] = dis[cur] + g.getWeight(cur, w);
pq.add(new Node(w, dis[w]));
// 一个顶点可能存在多份 我们在优先队列中进行更新 这样的副作用是,我们后来在pq中取出顶点
// 这个顶点很可能之前已经被处理过了。
pre[w] = cur;
}
}
}
}
}
public boolean isConnectedTo(int v) {
g.validateVertex(v);
return visited[v]; // 其实是判断连通性,如果是连通的,早晚会设置为true
}
public int disTo(int v) {
// 返回起点到顶点v的最短距离
g.validateVertex(v);
return dis[v];
}
public Iterable<Integer> path(int t) {
// 返回起点s 到 顶点t 的具体路径
ArrayList<Integer> result = new ArrayList<>();
if (!isConnectedTo(t))
return result;
int cur = t;
while (cur != s) {
result.add(cur);
cur = pre[cur];
}
result.add(s);
Collections.reverse(result);
return result;
}
public static void main(String[] args) {
WeightedGraph g = new WeightedGraph("g6.txt");
Dijkstra2 dijkstra = new Dijkstra2(g, 0);
for (int v = 0; v < g.V(); v++)
System.out.printf("%d ", dijkstra.disTo(v));
System.out.println();
System.out.println(dijkstra.path(3));
}
}
如果我们只关注从 s 到 t 之间的最短路径? 我们可以在循环中提前终止。
如果求所有点对 最短路径? --> 运行 V 次Dijkstra 算法 v*ElogE
整型溢出 --> Integer.MAX_VALUE 并不是正无穷 改进方式:用long 的最大值,用大整数类,或者设置一些标志。