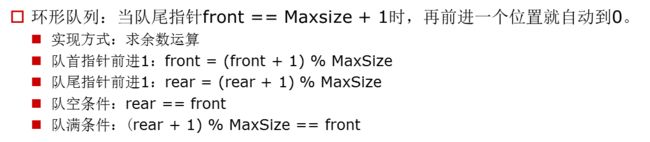数据结构&算法_堆、栈(堆栈)、队列、链表
堆:
①堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质:
·堆中某个节点的值总是不大于或不小于其父节点的值;
·堆总是一棵完全二叉树。将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。常见的堆有二叉堆、斐波那契堆等。
②堆是在程序运行时,而不是在程序编译时,申请某个大小的内存空间。即动态分配内存,对其访问和对一般内存的访问没有区别。
③堆是应用程序在运行的时候请求操作系统分配给自己内存,一般是申请/给予的过程。
④堆是指程序运行时申请的动态内存,而栈只是指一种使用堆的方法(即先进后出)。
堆的应用:
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
|
栈:
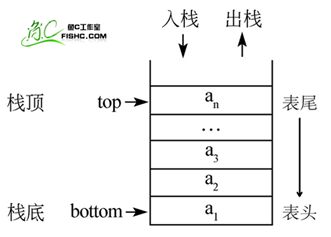
①栈(stack)又名堆栈,一个数据集合,可以理解为只能在一端进行插入或删除操作的列表。其限制是仅允许在表的一端进行插入和删除运算。这一端被称为栈顶,相对地,把另一端称为栈底。
②栈就是一个桶,后放进去的先拿出来,它下面本来有的东西要等它出来之后才能出来(先进后出)
③栈(Stack)是操作系统在建立某个进程时或者线程(在支持多线程的操作系统中是线程)为这个线程建立的存储区域,该区域具有FIFO的特性,在编译的时候可以指定需要的Stack的大小。
栈的基本操作:
进栈(压栈):push
出栈:pop
取栈顶:gettop
用python实现堆栈
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
|
栈的应用——括号匹配问题
括号匹配问题:给一个字符串,其中包含小括号、中括号、大括号,求该字符串中的括号是否匹配。例如:
()()[]{} 匹配
([{()}]) 匹配
[]( 不匹配
[(]) 不匹配
![]() 栈的应用——括号匹配问题
栈的应用——括号匹配问题
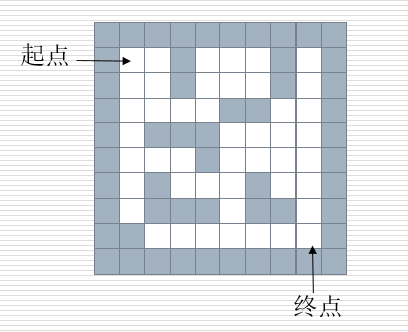
栈的应用——迷宫问题
![]() 栈的应用__迷宫问题
栈的应用__迷宫问题
队列
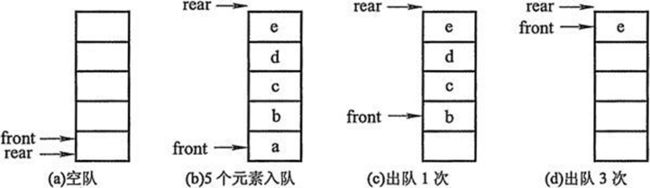
- 队列(Queue)是一个数据集合,仅允许在列表的一端进行插入,另一端进行删除。
- 进行插入的一端称为队尾(rear),插入动作称为进队或入队
- 进行删除的一端称为队头(front),删除动作称为出队
- 队列的性质:先进先出(First-in, First-out)
- 双向队列:队列的两端都允许进行进队和出队操作
使用方法:from collections import deque
创建队列:queue = deque(li)
进队:append
出队:popleft
双向队列队首进队:appendleft
双向队列队尾进队:pop
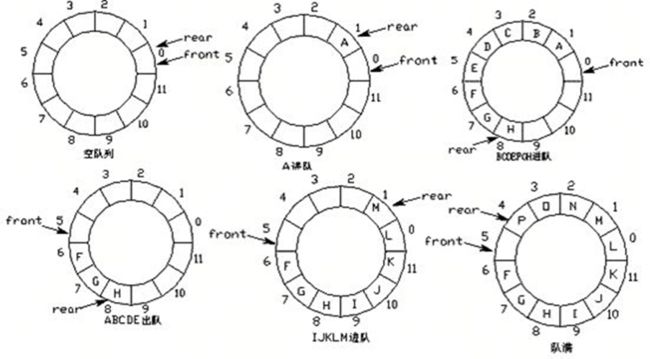
队列的实现原理
队列的实现原理:环形队列
队列的应用:
![]() 队列的应用--队列解决迷宫问题
队列的应用--队列解决迷宫问题
链表
链表中每一个元素都是一个对象,每个对象称为一个节点,包含有数据域key和指向下一个节点的指针next。通过各个节点之间的相互连接,最终串联成一个链表。
节点的定义:
| 1 2 3 4 |
|
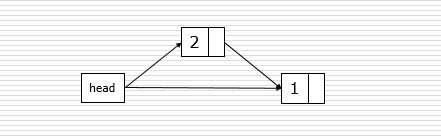
头节点:
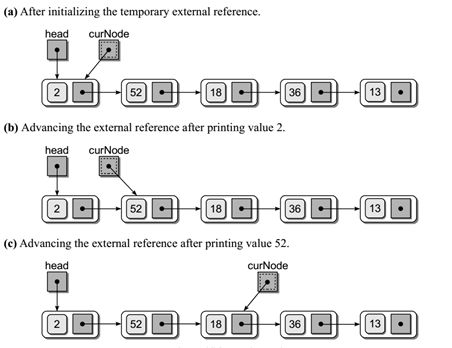
链表的遍历:
| 1 2 3 4 5 6 |
|
链表节点的插入和删除
| 1 2 3 4 5 6 7 8 |
|
建立链表
| 1 2 3 4 5 6 7 8 |
|
| 1 2 3 4 5 6 7 8 |
|
双链表
双链表中每个节点有两个指针:一个指向后面节点、一个指向前面节点。
节点定义:
| 1 2 3 4 5 |
|
双链表的插入和删除
| 1 2 3 4 5 6 7 8 9 10 11 |
|
建立双链表
| 1 2 3 4 5 6 7 8 9 |
|
栈与队列的异同
栈(Stack)和队列(Queue)是两种操作受限的线性表。
(线性表:线性表是一种线性结构,它是一个含有n≥0个结点的有限序列,同一个线性表中的数据元素数据类型相同并且满足“一对一”的逻辑关系。
“一对一”的逻辑关系指的是对于其中的结点,有且仅有一个开始结点没有前驱但有一个后继结点,有且仅有一个终端结点没有后继但有一个前驱结点,其它的结点都有且仅有一个前驱和一个后继结点。)
这种受限表现在:栈的插入和删除操作只允许在表的尾端进行(在栈中成为“栈顶”),满足“FIFO:First In Last Out”;队列只允许在表尾插入数据元素,在表头删除数据元素,满足“First In First Out”。
栈与队列的相同点:
1.都是线性结构。
2.插入操作都是限定在表尾进行。
3.都可以通过顺序结构和链式结构实现。、
4.插入与删除的时间复杂度都是O(1),在空间复杂度上两者也一样。
5.多链栈和多链队列的管理模式可以相同。
栈与队列的不同点:
1.删除数据元素的位置不同,栈的删除操作在表尾进行,队列的删除操作在表头进行。
2.应用场景不同;常见栈的应用场景包括括号问题的求解,表达式的转换和求值,函数调用和递归实现,深度优先搜索遍历等;常见的队列的应用场景包括计算机系统中各种资源的管理,消息缓冲器的管理和广度优先搜索遍历等。
3.顺序栈能够实现多栈空间共享,而顺序队列不能。