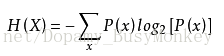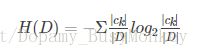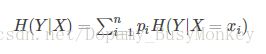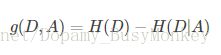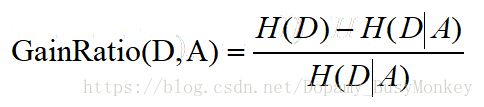决策树

https://baike.baidu.com/item/%E9%A6%99%E5%86%9C%E7%86%B5/1649961?fr=aladdin

https://blog.csdn.net/jiaoyangwm/article/details/79525237

https://blog.csdn.net/chichoxian/article/details/52017815

 

目录

1、香农熵：

2、数据集划分：将不同特征独立出来

3、信息增益：

4、最佳特征：信息增益最大的特征

5、ID3 算法构建决策树：

6、C4.5 算法构建决策树：

7、CART 算法构建决策树：

---

 

1、香农熵：

一条信息的信息量大小和它的不确定性有直接的关系。比如说，我们要搞清楚一件非常非常不确定的事，或是我们一无所知的事情，就需要了解大量的信息。相反，如果我们对某件事已经有了较多的了解，我们不需要太多的信息就能把它搞清楚。所以，从这个角度，我们可以认为，信息量的度量就等于不确定性的多少。

变量的不确定性越大，熵也就越大，把它搞清楚所需要的信息量也就越大。

from math import log

def creatDataSet():
    dataSet=[[0, 0, 0, 0, 'no'],
            [0, 0, 0, 1, 'no'],
            [0, 1, 0, 1, 'yes'],
            [0, 1, 1, 0, 'yes'],
            [0, 0, 0, 0, 'no'],
            [1, 0, 0, 0, 'no'],
            [1, 0, 0, 1, 'no'],
            [1, 1, 1, 1, 'yes'],
            [1, 0, 1, 2, 'yes'],
            [1, 0, 1, 2, 'yes'],
            [2, 0, 1, 2, 'yes'],
            [2, 0, 1, 1, 'yes'],
            [2, 1, 0, 1, 'yes'],
            [2, 1, 0, 2, 'yes'],
            [2, 0, 0, 0, 'no']]
    labels=['年龄','有工作','有自己的房子','信贷情况']
    return dataSet,labels

def calcShannonEnt(dataSet):
    numEntries=len(dataSet)
    labelCounts={}
    for featVec in dataSet:
        currentLabel=featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel]=0
        labelCounts[currentLabel]+=1

    shannonEnt=0.0
    for key in labelCounts:
        prob=float(labelCounts[key])/numEntries
        shannonEnt-=prob*log(prob,2)
    return shannonEnt

if __name__=='__main__':
    dataSet,features=creatDataSet()
    print(dataSet)
    print(calcShannonEnt(dataSet))

2、数据集划分：将不同特征独立出来

输入：待划分的数据集、划分数据集的特征、需要返回的特征的值

数据集dataSet：第一列为第一特征（no surfacing）、第二列为第二特征（flippers）、第三列为改行结果是否是鱼

# coding:utf-8
from math import log

def createDataSet():
    dataSet = [[1,1,'yes'],
              [1,1,'yes'],
              [1,0,'no'],
              [0,1,'no'],
              [0,1,'no']]
    labels = ['no surfacing','flippers']
    return dataSet, labels

def calcShannonEnt(dataSet):
    countDataSet = len(dataSet)
    labelCounts={}
    for featVec in dataSet:
        currentLabel=featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    print labelCounts

    shannonEnt = 0.0

    for key in labelCounts:
        prob = float(labelCounts[key])/countDataSet
        shannonEnt -= prob * log(prob,2)
    return shannonEnt


def splitDataSet(dataSet,axis,value):
    retDataSet = []

    for featVec in dataSet:
        if featVec[axis] == value:
            reduceFeatVec = featVec[:axis]
            reduceFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reduceFeatVec)

    return retDataSet

if __name__=='__main__':
    dataSet,features=createDataSet()
    print(dataSet)
    print(splitDataSet(dataSet,0,1))

3、信息增益：

• 经验熵：已知数据集的数学期望，比如在2数据集中yes 和 no 两个了类别的数学期望（k为类别计数）

• 条件熵：已知随机变量X的条件下随机变量Y的不确定性，随机变量X给定的条件下随机变量Y的条件熵(conditional entropy) H(Y|X)，定义X给定条件下Y的条件概率分布的熵对X的数学期望。比如2数据集中，特征1有两个分布1和0，将特征1为1的数据集获取到，求熵，同理特征1为0的数据集（x为某一特征的分布计数，i为特征计数）

• 信息增益：信息增益是相对于特征而言的。所以，特征A对训练数据集D的信息增益g(D,A)，定义为集合D的经验熵H(D)与特征A给定条件下D的经验条件熵H(D|A)之差。在信息增益中，衡量标准是看特征能够为分类系统带来多少信息，带来的信息越多，该特征越重要。对一个特征而言，系统有它和没它时信息量将发生变化，而前后信息量的差值就是这个特征给系统带来的信息量。所谓信息量，就是熵。

4、最佳特征：信息增益最大的特征

将数据集的所有特征依次用splitDataSet划分，并且分别求出信息增益，并记录信息增益最大的一个特征划分

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0
    bestFeature = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntropy
        if (infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature

5、ID3 算法构建决策树：

ID3采用信息增益作为选择最优的分裂属性的方法

停止条件：

• 最小节点数：当节点的数据量小于一个指定的数量时，不继续分裂。两个原因：一是数据量较少时，再做分裂容易强化噪声数据的作用；二是降低树生长的复杂性。提前结束分裂一定程度上有利于降低过拟合的影响。
• 熵或者基尼值小于阀值：由上述可知，熵和基尼值的大小表示数据的复杂程度，当熵或者基尼值过小时，表示数据的纯度比较大，如果熵或者基尼值小于一定程度时，节点停止分裂。
• 决策树的深度达到指定的条件：节点的深度可以理解为节点与决策树跟节点的距离，如根节点的子节点的深度为1，因为这些节点与跟节点的距离为1，子节点的深度要比父节点的深度大1。决策树的深度是所有叶子节点的最大深度，当深度到达指定的上限大小时，停止分裂。
• 所有特征已经使用完毕，不能继续进行分裂：被动式停止分裂的条件，当已经没有可分的属性时，直接将当前节点设置为叶子节点。
• 该群数据已经找不到新的属性进行节点分割，该群数据没有任何未处理的数据。

createTree代码分析：

先找到最大信息增益特征，然后通过该特征的数据集划分，分别对划分的数据集进行最大信息增益计算，直到满足以上停止条件后结束递归调用。

# coding:utf-8
from math import log
import operator

def createDataSet():
    dataSet = [[1,1,'yes'],
              [1,1,'yes'],
              [1,0,'no'],
              [0,1,'no'],
              [0,1,'no']]
    labels = ['no surfacing','flippers']
    return dataSet, labels

def calcShannonEnt(dataSet):
    countDataSet = len(dataSet)
    labelCounts={}
    for featVec in dataSet:
        currentLabel=featVec[-1]
        if currentLabel not in labelCounts.keys():
            labelCounts[currentLabel] = 0
        labelCounts[currentLabel] += 1
    print labelCounts

    shannonEnt = 0.0

    for key in labelCounts:
        prob = float(labelCounts[key])/countDataSet
        shannonEnt -= prob * log(prob,2)
    return shannonEnt


def splitDataSet(dataSet,axis,value):
    retDataSet = []

    for featVec in dataSet:
        if featVec[axis] == value:
            reduceFeatVec = featVec[:axis]
            reduceFeatVec.extend(featVec[axis+1:])
            retDataSet.append(reduceFeatVec)

    return retDataSet

def chooseBestFeatureToSplit(dataSet):
    numFeatures = len(dataSet[0]) - 1
    baseEntropy = calcShannonEnt(dataSet)
    bestInfoGain = 0.0
    bestFeature = -1
    for i in range(numFeatures):
        featList = [example[i] for example in dataSet]
        uniqueVals = set(featList)
        newEntropy = 0.0
        for value in uniqueVals:
            subDataSet = splitDataSet(dataSet, i, value)
            prob = len(subDataSet)/float(len(dataSet))
            newEntropy += prob * calcShannonEnt(subDataSet)
        infoGain = baseEntropy - newEntropy
        if (infoGain > bestInfoGain):
            bestInfoGain = infoGain
            bestFeature = i
    return bestFeature

def majorityCnt(classList):
    classCount={}
    for vote in classList:
        if vote not in classCount.keys():
            classCount[vote] = 0
        classCount[vote] += 1
        sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1),reverse=True)

    return sortedClassCount[0][0]


def createTree(dataSet,labels):
    classList = [example[-1] for example in dataSet]
    if classList.count(classList[0]) == len (classList):
        return classList[0]
    if len(dataSet[0]) == 1:
        return majorityCnt(classList)
    bestFeat = chooseBestFeatureToSplit(dataSet)
    bestFeatLabel = labels[bestFeat]
    myTree = {bestFeatLabel:{}}
    del(labels[bestFeat])
    featValues = [example[bestFeat] for example in dataSet]
    uniqueVals = set(featValues)
    for value in uniqueVals:
        subLabels = labels[:]
        myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),subLabels)
    return myTree

if __name__=='__main__':
    dataSet,features=createDataSet()
    print(createTree(dataSet,features))

6、C4.5 算法构建决策树：

C4.5选择具有最大增益率的属性作为分裂属性

• 信息增益率：

7、CART 算法构建决策树：

无论是分类树还是回归树，CART都要选择使子节点的GINI值或者回归方差最小的属性作为分裂的方案。即最小化（分类树）

• Gini基尼指数：

• 回归方差公式：

• Gain增益：

• 回归树：