Javascript中的Number类型和BigInt类型

Number

Number类型使用IEEE 754 双精度 64 位浮点数格式来表示整数和浮点值，它由64位组成，这64位由3部分组成，（S：符号位，Exponent:指数域，Fraction：尾数域）。

因为这样的特性，使得js在计算方面存在两个限制：
1.当十进制小数的二进制表示的有限数字超过 52 位时，在 JavaScript 里是不能精确存储的，这时候就存在舍入误差(Round-off error)
2.数字的最大值和最小值收到限制。

舍入误差

先看第一个问题，也是最为经典的 ：为什么在js中 0.1 + 0.2 == 0.3 的判断结果为 false？

因为对于计算机而言，两个数字在相加时是以二进制形式进行的，在呈现结果时才转换成十进制。

十进制小数转换为二进制小数：用2乘十进制小数，可以得到积，将积的整数部分取出，再用2乘余下的小数部分，又得到一个积，再将积的整数部分取出，如此进行，直到积中的小数部分为零，此时0或1为二进制的最后一位。或者达到所要求的精度为止。

如：0.7=（0.1 0110 0110...）B
0.7*2=1.4========取出整数部分1
0.4*2=0.8========取出整数部分0
0.8*2=1.6========取出整数部分1
0.6*2=1.2========取出整数部分1
0.2*2=0.4========取出整数部分0
0.4*2=0.8========取出整数部分0
0.8*2=1.6========取出整数部分1
0.6*2=1.2========取出整数部分1
0.2*2=0.4========取出整数部分0

 // 0.1 转化为二进制
0.0 0011 0011 0011 0011...(0011无限循环）

// 0.2 转化为二进制
0.0011 0011 0011 0011 0011...(0011无限循环）

由于尾数只有52位，所以对于0.1和0.2转换后的二进制如下：

e = -4; m =1.1001100110011001100110011001100110011001100110011010 (52位)
e = -3; m =1.1001100110011001100110011001100110011001100110011010 (52位)

像十进制数有4舍5入的规则一样，二进制也存在类似的规则，简单的说，如果 1.101 
要保留一位小数，可能的值是 1.1 和 1.2，那么先看 1.101 和 1.1 或者 1.2 哪个值更
接近，毫无疑问是 1.1，于是答案是 1.1。那么如果要保留两位小数呢？很显然要么
是 1.10 要么是 1.11，而且又一样近，这时就要看这两个数哪个是偶数（末位是偶
数），保留偶数为答案。综上，如果第 52 bit 和 53 bit 都是 1，那么是要进位的。
这也导致了误差的产生。

我们看下这两个二进制数相加

√  e = -4; m = 1.1001100110011001100110011001100110011001100110011010 (52位)
+ e = -3; m = 1.1001100110011001100110011001100110011001100110011010 (52位)
---------------------------------------------------------------------------
相加时如果指数不一致，需要对齐，一般情况下是向右移，因为最右边的即使溢出了，损失的精度远远小于左边溢出。
  e = -3; m = 0.1100110011001100110011001100110011001100110011001101 
+ e = -3; m = 1.1001100110011001100110011001100110011001100110011010
---------------------------------------------------------------------------
  e = -3; m = 10.0110011001100110011001100110011001100110011001100111
---------------------------------------------------------------------------
  e = -2; m = 1.0011001100110011001100110011001100110011001100110100(52位)
---------------------------------------------------------------------------
= 0.010011001100110011001100110011001100110011001100110100
= 0.30000000000000004(十进制)

这就解释了舍入误差产生的原因。

要解决这个问题，最好的方法是设置一个误差范围值，通常称为”机器精度“，而对于Javascript来说，这个值通常是2^-52,而在ES6中，已经为我们提供了这样一个

属性：Number.EPSILON，而这个值正等于2^-52。这个值非常非常小，在底层计算机已经帮我们运算好，并且无限接近0，但不等于0,。这个时候我们只要判断(0.1+0.2)-0.3小于

Number.EPSILON，在这个误差的范围内就可以判定0.1+0.2===0.3为true。

  function numbersequal(a,b){
      return Math.abs(a-b)<Number.EPSILON;
  } 
  var a=0.1+0.2， b=0.3;
  console.log(numbersequal(a,b)); //true

大数运算与BigInt

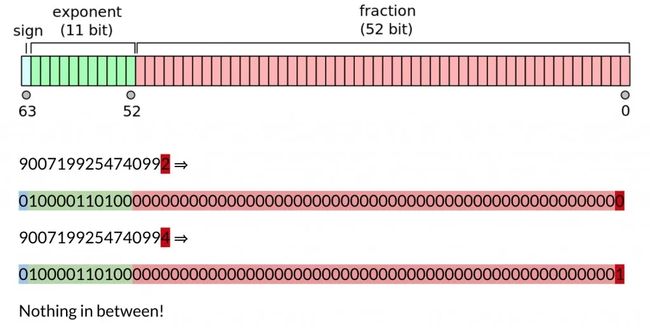
JS 中的Number类型只能安全地表示-9007199254740991 (-(2^53-1)) 和9007199254740991(2^53-1)之间的整数，任何超出此范围的整数值都可能失去精度。

JS 提供Number.MAX_SAFE_INTEGER常量来表示 最大安全整数，Number.MIN_SAFE_INTEGER常量表示最小安全整数：

const minInt = Number.MIN_SAFE_INTEGER;

console.log(minInt);         // → -9007199254740991

console.log(minInt - 5);     // → -9007199254740996

// notice how this outputs the same value as above
console.log(minInt - 4);     // → -9007199254740996

BigInt类型的出现正是为了解决此类问题.
要创建BigInt，只需在整数的末尾追加n即可:

console.log(9007199254740995n);    // → 9007199254740995n
console.log(9007199254740995);     // → 9007199254740996

console.log(9007199254740991n + 2n);  // 9007199254740993n 正确

或者，可以调用BigInt()构造函数

BigInt("9007199254740995");    // → 9007199254740995n

BigInt文字也可以用二进制、八进制或十六进制表示

// binary
console.log(0b100000000000000000000000000000000000000000000000000011n);
// → 9007199254740995n

// hex
console.log(0x20000000000003n);
// → 9007199254740995n

// octal
console.log(0o400000000000000003n);
// → 9007199254740995n

// note that legacy octal syntax is not supported
console.log(0400000000000000003n);
// → SyntaxError

记住，不能使用严格的相等运算符来比较BigInt和普通数字，因为它们不是同一类型的:

console.log(10n === 10);    // → false

console.log(typeof 10n);    // → bigint
console.log(typeof 10);     // → number

相反，你可以使用相等运算符，它在处理操作数之前执行隐式类型转换:

console.log(10n == 10);    // → true

所有算术运算符都可以在BigInt上使用，除了一元加号(+)运算符:

10n + 20n;    // → 30n
10n - 20n;    // → -10n
+10n;         // → TypeError: Cannot convert a BigInt value to a number
-10n;         // → -10n
10n * 20n;    // → 200n
20n / 10n;    // → 2n
23n % 10n;    // → 3n
10n ** 3n;    // → 1000n

let x = 10n;
++x;          // → 11n
--x;          // → 10n

不支持一元加号(+)运算符的原因是，有些程序可能依赖于这样的结果：+总是产生Number类型的值，或者抛出异常。改变+ 的行为也会破坏asm.js代码。

当然，当与BigInt操作数一起使用时，算术运算符应该返回一个BigInt值。因此，除法(/)运算符的结果会自动四舍五入到最接近的整数。例如:

25 / 10;      // → 2.5
25n / 10n;    // → 2n

隐式类型转换

因为隐式类型转换可能丢失信息，所以不允许BigInt和Number之间的混合操作。当混合使用大整数和浮点数时，结果值可能无法用BigInt或Number准确表示。看看下面的例子:

(9007199254740992n + 1n) + 0.5

这个表达式的结果在BigInt和Number的范围之外。带有小数部分的Number不能准确地转换为BigInt。大于253的BigInt不能准确转换为Number。

由于这个限制，不能使用Number和 BigInt操作数的组合来执行算术运算。你也不能将 BigInt传递给Web API和期望Number类型参数的内置JavaScript函数。试图这样做会导致TypeError:

10 + 10n;    // → TypeError
Math.max(2n, 4n, 6n);    // → TypeError

注意，关系运算符不遵循此规则，如下例所示:

10n > 5;    // → true

如果希望使用BigInt和 Number执行算术计算，首先需要确定应该在哪个域中执行操作。为此，只需通过调用Number()或BigInt()来转换操作数:

BigInt(10) + 10n;    // → 20n
// or
10 + Number(10n);    // → 20

当遇到Boolean上下文时，BigInt被视为类似于Number。换句话说，只要不是0n， BigInt就被认为是一个布尔真值:

if (5n) {
     
    // 这个代码块将被执行
}

if (0n) {
     
    // 但这个不会
}

对BigInt和 Number进行排序时，不会发生隐式类型转换:

const arr = [3n, 4, 2, 1n, 0, -1n];

arr.sort();    // → [-1n, 0, 1n, 2, 3n, 4]

按位运算符如|, &, <<, >>和 ^ 操作 BigInt与Number类似。负数被解释为无穷长二进制补码。不允许混合操作数。以下是一些例子:

90 | 115;      // → 123
90n | 115n;    // → 123n
90n | 115;     // → TypeError

BigInt构造函数

与其他基本类型一样，可以使用构造函数创建BigInt。如果可能，传递给BigInt的参数会自动转换为BigInt:

BigInt("10");    // → 10n
BigInt(10);      // → 10n
BigInt(true);    // → 1n

无法转换的数据类型和值会抛出异常:

BigInt(10.2);     // → RangeError
BigInt(null);     // → TypeError
BigInt("abc");    // → SyntaxError

你可以直接对通过BigInt 构造函数创建的变量执行算术运算：

BigInt(10) * 10n;    // → 100n

当用作严格相等运算符的操作数时，使用构造函数创建的BigInt操作数与常规操作数类似:

BigInt(true) === 1n;    // → true

库函数

JavaScript提供了两个库函数来把BigInt值表示为有符号或无符号整数:

BigInt.asUintN(width, BigInt): 包装一个介于 0 和 2width-1之间的 BigInt
BigInt.asIntN(width, BigInt): 包装一个介于 -2width-1 和2width-1-1之间的BigInt
这些函数在执行64位算术操作时特别有用。这样你就可以保持在预定的范围内。

浏览器支持及转换

在撰写本文时，Chrome +67和Opera +54完全支持BigInt 数据类型。不幸的是，Edge和Safari还没有实现它。火狐默认不支持BigInt ，但可以通过在about:config中将javascript.options.bigint设置为true来启用。支持的浏览器的最新列表可以在Can I use…上找到。

不幸的是，转换BigInt 是一个极其复杂的过程，这会导致严重的运行时性能损失。也不可能直接填充BigInt ，因为该提议改变了几个现有操作符的行为。目前，更好的选择是使用JSBI库，它是BigInt 建议的纯JavaScript 实现。

这个库提供了一个与内置BigInt 行为完全相同的API。下面是使用JSBI的方法:

import JSBI from './jsbi.mjs';

const b1 = JSBI.BigInt(Number.MAX_SAFE_INTEGER);
const b2 = JSBI.BigInt('10');

const result = JSBI.add(b1, b2);

console.log(String(result));    // → '9007199254741001'

使用JSBI的一个优点是，一旦浏览器支持得到改进，你就不需要重写代码了。相反，您可以使用babel plugin将你的JSBI代码自动编译成本地的BigInt 代码。此外，JSBI的性能与内置的BigInt 实现相当。你可以期待更广泛的浏览器支持BigInt 。

结论

BigInt是一种新的数据类型，用于当整数值大于Number 数据类型支持的范围时。这种数据类型允许我们安全地对大整数执行算术操作，表示高精度时间戳，使用大整数 ID 等等，而不需要使用库。

重要的是要记住，不能使用Number和BigInt操作数的组合来执行算术运算。你需要通过显式转换操作数来确定操作应该在哪个域中执行。此外，出于兼容性的原因，不允许在BigInt上使用一元加号(+)操作符。