ROC曲线的理解与绘制
什么是ROC曲线?
ROC曲线:接收者操作特征(receiver operating characteristic),roc曲线上每个点反映着对同一信号刺激的感受性。
首先,在试图弄懂AUC和ROC曲线之前,一定要彻底理解混淆矩阵的定义!
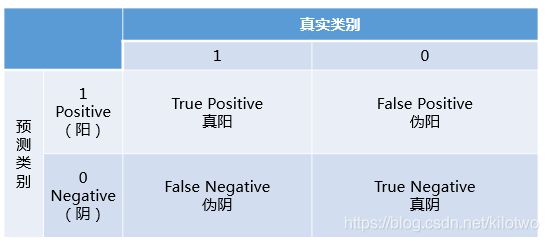
混淆矩阵中有着Positive、Negative、True、False的概念,其意义如下:
- 称预测类别为1的为Positive(阳性),预测类别为0的为Negative(阴性)。
- 预测正确的为True(真),预测错误的为False(伪)。
对上述概念进行组合,就产生了如下的混淆矩阵:
然后,由此引出True Positive Rate(真阳率)、False Positive(伪阳率)两个概念:
仔细看这两个公式,发现其实TPRate就是TP除以TP所在的列,FPRate就是FP除以FP所在的列,二者意义如下:
-
**TPRate的意义是所有真实类别为1的样本中,预测类别为1的比例。**Sensitivity
TPR: TP/(TP+FN)
-
**FPRate的意义是所有真实类别为0的样本中,预测类别为1的比例。**1-Specificity
FPR: FP/(FP+TN)
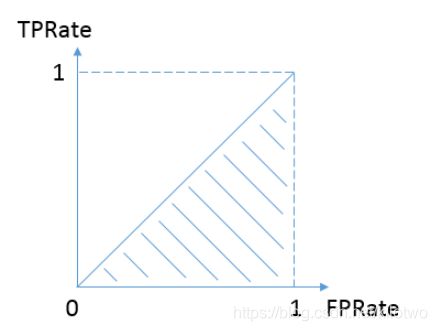
按照定义,AUC即ROC曲线下的面积,而ROC曲线的横轴是FPRate,纵轴是TPRate,当二者相等时,即y=x,如下图:
横轴:假正类率(false postive rate FPR)——特异度,(1-Specificity)
纵轴:真正类率(true postive rate TPR)——灵敏度,Sensitivity(正类覆盖率)(又是召回率recall)
真负类率(True Negative Rate)TNR: TN/(FP+TN),代表分类器预测的负类中实际负实例占所有负实例的比例,TNR=1-FPR。Specificity
上图表示的意义是:对于不论真实类别是1还是0的样本,分类器预测为1的概率是相等的。
换句话说,分类器对于正例和负例毫无区分能力,和抛硬币没什么区别,一个抛硬币的分类器是我们能想象的最差的情况,因此一般来说我们认为AUC的最小值为0.5(当然也存在预测相反这种极端的情况,AUC小于0.5,这种情况相当于分类器总是把对的说成错的,错的认为是对的,那么只要把预测类别取反,便得到了一个AUC大于0.5的分类器)。
而我们希望分类器达到的效果是:对于真实类别为1的样本,分类器预测为1的概率(即TPRate),要大于真实类别为0而预测类别为1的概率(即FPRate),即y>x,因此大部分的ROC曲线长成下面这个样子:
最理想的情况下,既没有真实类别为1而错分为0的样本——TPRate一直为1,也没有真实类别为0而错分为1的样本——FPRate一直为0,AUC为1,这便是AUC的极大值。
假设采用逻辑回归分类器,其给出针对每个实例为正类的概率,那么通过设定一个阈值如0.6,概率大于等于0.6的为正类,小于0.6的为负类。对应的就可以算出一组(FPR,TPR),在平面中得到对应坐标点。随着阈值的逐渐减小,越来越多的实例被划分为正类,但是这些正类中同样也掺杂着真正的负实例,即TPR和FPR会同时增大。阈值最大时,对应坐标点为(0,0),阈值最小时,对应坐标点(1,1)。
不妨举个简单的例子。
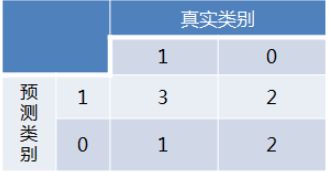
首先对于硬分类器(例如SVM,NB),预测类别为离散标签,对于8个样本的预测情况如下:

得到混淆矩阵如下:
进而算得TPRate=3/4,FPRate=2/4,得到ROC曲线:
对于LR等预测类别为概率的分类器,依然用上述例子,假设预测结果如下:
这时,需要设置阈值来得到混淆矩阵,不同的阈值会影响得到的TPRate,FPRate,如果阈值取0.5,小于0.5的为0,否则为1,那么我们就得到了与之前一样的混淆矩阵。其他的阈值就不再啰嗦了。依次使用所有预测值作为阈值,得到一系列TPRate,FPRate,描点,求面积,即可得到AUC。
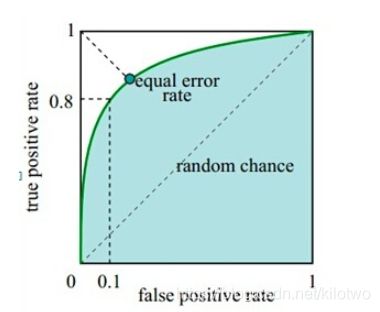
如下面这幅图,图中实线为ROC曲线,线上每个点对应一个阈值。
横轴FPR:1-TNR,1-Specificity,FPR越大,预测正类中实际负类越多(把对的当成错的)。
纵轴TPR:Sensitivity(正类覆盖率),TPR越大,预测正类中实际正类越多\。
理想目标:TPR=1,FPR=0,即图中(0,1)点,故ROC曲线越靠拢(0,1)点,越偏离45度对角线越好,Sensitivity、Specificity越大效果越好
最后说说AUC的优势,AUC的计算方法同时考虑了分类器对于正例和负例的分类能力,在样本不平衡的情况下,依然能够对分类器作出合理的评价。
例如在反欺诈场景,设欺诈类样本为正例,正例占比很少(假设0.1%),如果使用准确率评估,把所有的样本预测为负例,便可以获得99.9%的准确率。
但是如果使用AUC,把所有样本预测为负例,TPRate和FPRate同时为0(没有Positive),与(0,0) (1,1)连接,得出AUC仅为0.5,成功规避了样本不均匀带来的问题。
ROC曲线绘制的Python实现
熟悉sklearn的读者肯定都知道,几乎所有评估模型的指标都来自sklearn库下面的metrics,包括计算召回率,精确率等。ROC曲线的绘制也不例外,都得先计算出评估的指标,也就是从metrics里面去调用roc_curve, auc,然后再去绘制。
from sklearn.metrics import roc_curve, auc
roc_curve和auc的官方说明教程示例如下。
# 数据准备
>>> import numpy as np
>>> from sklearn import metrics
>>> y = np.array([1, 1, 2, 2])
>>> scores = np.array([0.1, 0.4, 0.35, 0.8])
# roc_curve的输入为
# y: 样本标签
# scores: 模型对样本属于正例的概率输出
# pos_label: 标记为正例的标签,本例中标记为2的即为正例
>>> fpr, tpr, thresholds = metrics.roc_curve(y, scores, pos_label=2)
# 假阳性率
>>> fpr
array([ 0. , 0.5, 0.5, 1. ])
# 真阳性率
>>> tpr
array([ 0.5, 0.5, 1. , 1. ])
# 阈值
>>> thresholds
array([ 0.8 , 0.4 , 0.35, 0.1 ])
# auc的输入为很简单,就是fpr, tpr值
>>> auc = metrics.auc(fpr, tpr)
>>> auc
0.75
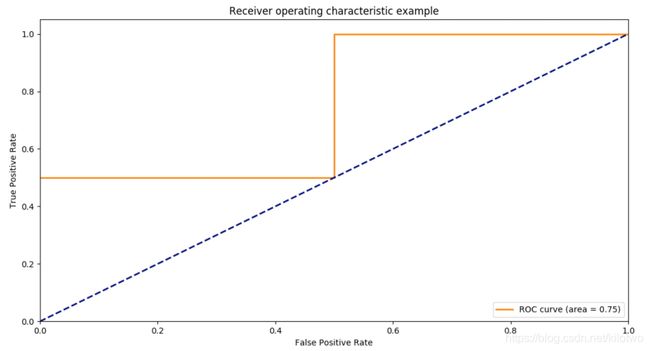
因此调用完roc_curve以后,我们就齐全了绘制ROC曲线的数据。接下来的事情就很简单了,调用plt即可,还是用官方的代码示例一步到底。
import matplotlib.pyplot as plt
plt.figure()
lw = 2
plt.plot(fpr, tpr, color='darkorange',
lw=lw, label='ROC curve (area = %0.2f)' % auc)
plt.plot([0, 1], [0, 1], color='navy', lw=lw, linestyle='--')
plt.xlim([0.0, 1.0])
plt.ylim([0.0, 1.05])
plt.xlabel('False Positive Rate')
plt.ylabel('True Positive Rate')
plt.title('Receiver operating characteristic example')
plt.legend(loc="lower right")
plt.show()
最终生成的ROC曲线结果如下图。
学习自:
https://www.zhihu.com/question/39840928/answer/241440370
https://www.jianshu.com/p/2ca96fce7e81