组队学习7:自然语言处理NLP(一)
组队学习介绍
最近又懒惰了(虽然确实事情也多),好久没有空更新博客,遂报名公众号 Datawhale 的 NLP 学习小组来督促自己学习。学习小组的目的主要是细致地学习 NLP 的一些概念,更好地巩固自己的文本挖掘能力。
学习小组的时间安排大致如下:
-
Task 1: Introduction and Word Vectors (3天)
- 理论部分
- 介绍NLP研究的对象
- 如何表示单词的含义
- Word2Vec方法的基本原理
- 视频教程
- youtube video
- bilibili video
- 资源
- slides
- official notes
- 问题解答区
- 理论部分
-
Task 2: Word Vectors and Word Senses (3天)
- 理论部分
- 回顾 Word2Vec模型
- 介绍 count based global matrix factorization 方法
- 介绍 GloVe 模型
- 视频教程
- youtube video
- bilibili video
- 资源
- slides
- official notes
- 问题解答区
- 理论部分
-
Task 3: Subword Models (3天)
- 理论部分
- 回顾 word2vec 和 glove,并介绍其所存在问题
- 介绍 n-gram 思想
- 介绍 FastText 模型
- 视频教程
- youtube video
- bilibili video
- 资源
- slides
- official notes
- 问题解答区
- 理论部分
-
Task 4: Contextual Word Embeddings (3天)
- 理论部分
- 回顾 Word2Vec, GloVe, fastText 模型
- 介绍contextual word representation
- 介绍 ELMO,GPT与BERT模型
- 视频教程
- youtube video
- bilibili video
- 资源
- slides
- official notes
- 问题解答区
- 理论部分
-
Task 5: Homework (3天)(组队完成)
这两天实在有点忙,就借鉴了一下 Datawhale-浩浩雷 助教撰写的文案。希望不要拿到飞机票!
Word2vec introduction
Word vectors
我们将为每个单词构建一个稠密的向量,使得它能够与相似文本里的词向量相近,word meaning 作为一种神经词向量,在我们对向量空间进行可视化:
注:word vector 有时也叫做 word embedding 或者 word representations,他们都是一种表示结构。
Word2vec:Overview
Word2vec(Mikolov et al. 2013) 是一种学习词向量的框架
-
包含大量的文本语料
-
固定词表中的每一个单词由一个词向量表示
-
文本中的每个单词位置 t,有一个中心词c,和它的上下文 o(除了 c 的外部单词)。
-
通过 c 和 o 的词向量相似性来计算 P(o/c)
-
不断的调整词向量,最大化概率
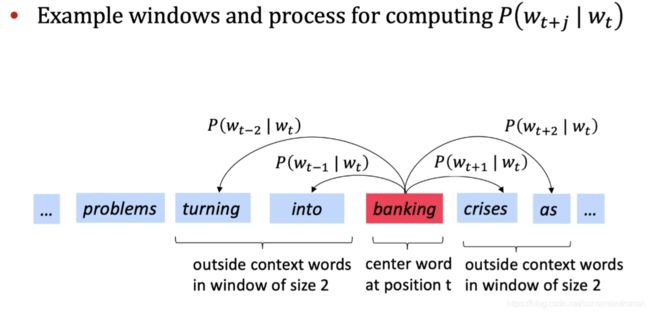
固定窗口,滑动窗口并计算:
Word2vec的目标函数:
对于每个位置 t = 1,…,T,固定窗口大小m,给定中心词wj:
l i k e l i h o o d = L ( θ ) = ∏ t = 1 T ∏ − m ≤ j ≤ m j ≠ 0 p ( w t + j ∣ w t ; θ ) likelihood=L(\theta)=\prod_{t=1}^{T}\prod_{-m \le j \le m\\ \ \ \ \ j\ne0}^{}p(w_{t+j}|w_t;\theta) likelihood=L(θ)=t=1∏T−m≤j≤m j=0∏p(wt+j∣wt;θ)
注:$ \theta $ 是需要优化的参数
J ( θ ) = − 1 T l o g L ( θ ) = − 1 T ∑ t = 1 T ∑ − m ≤ j ≤ m j ≠ 0 l o g P ( w t + j ∣ w t ; θ ) J(\theta)=-\frac 1TlogL(\theta)=-\frac1T\sum_{t=1}^T\sum_{-m\le j\le m \\ \ \ \ \ j\ne 0}logP(w_{t+j}|w_t;\theta) J(θ)=−T1logL(θ)=−T1t=1∑T−m≤j≤m j=0∑logP(wt+j∣wt;θ)
注:
- J ( θ ) J(\theta) J(θ)为损失函数(这里是平均负对数似然);
- 负号将极大化损失函数转化为极小化损失函数;
- log函数方便将乘法转化为求和(优化处理)
如何计算?
-
问:如何计算 P ( w t + j ∣ w t ; θ ) P(w_{t+j}|w_t;\theta) P(wt+j∣wt;θ)?
-
答:对于每个单词 w 我们使用两个向量 v w v_w vw 和 u w u_w uw
v w v_w vw :当 w 是中心词时
u w u_w uw :当 w 是上下文单词时
-
对于中心词 c 和上下文单词 o,有:
P ( o ∣ c ) = e x p ( u o T v c ) ∑ w ϵ V e x p ( u w T v c ) P(o|c)=\frac {exp(u_o^Tv_c)}{\sum_{w\epsilon V}exp(u_w^Tv_c)} P(o∣c)=∑wϵVexp(uwTvc)exp(uoTvc)
Example:
在概率函数中:
P ( o ∣ c ) = e x p ( u o T v c ) ∑ w ϵ V e x p ( u w T v c ) P(o|c)=\frac {exp(u_o^Tv_c)}{\sum_{w\epsilon V}exp(u_w^Tv_c)} P(o∣c)=∑wϵVexp(uwTvc)exp(uoTvc)
- 分子取幂函数使得始终可以为正
- 向量 u o u_o uo 和向量 v c v_c vc 点乘,点乘结果越大,向量之间越相似
- u T v = u ⋅ v = ∑ i = 1 n u i v i u^Tv=u·v=\sum_{i=1}^nu_iv_i uTv=u⋅v=∑i=1nuivi
- 对整个词表标准化,给出概率分布
softmax函数进行归一化(深度学习中常用): R n → R n \Bbb{R^n}\to \Bbb{R^n} Rn→Rn
s o f t m a x ( x ) = e x p ( x i ) ∑ j = 1 n e x p ( x j ) = p i softmax(x)= \frac {exp(x_i)}{\sum_{j=1}^nexp(x_j)}=p_i softmax(x)=∑j=1nexp(xj)exp(xi)=pi
注:用于将任意值 x i x_i xi 映射到概率分布 p i p_i pi
4. Word2vec objective function gradients
Training a model by optimizing parameters
(通过优化参数的方式训练模型)- 最小化损失
To train the model: Compute all vector gradients
整个模型里只有一个参数 θ \theta θ ,所以我们只用优化这一个参数就行。
例如:模型在一个 d 维,词典大小为 V :
θ = [ v a a r d v a r k v a ⋮ v z e b r a u a a r d v a r k u a ⋮ u z e b r a ] ϵ R 2 d V \theta=\begin{bmatrix}v_{aardvark}\\v_a\\\vdots\\v_{zebra}\\u_{aardvark}\\u_a\\\vdots\\u_{zebra} \end{bmatrix}\epsilon\ \Bbb R^{2dV} θ=⎣⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎡vaardvarkva⋮vzebrauaardvarkua⋮uzebra⎦⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎤ϵ R2dV
- 2:每个单词有两个向量
- 通过梯度(导数)下降的方式优化参数
- 梯度下降会用到链式法则
- 迭代计算每个中心词向量和上下文词向量随着滑动窗口移动的梯度
- 依次迭代更新窗口中所有的参数
Example:
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-5tmZO9ub-1593053167684)(img/image-20200607232818301.png)]
计算手稿:
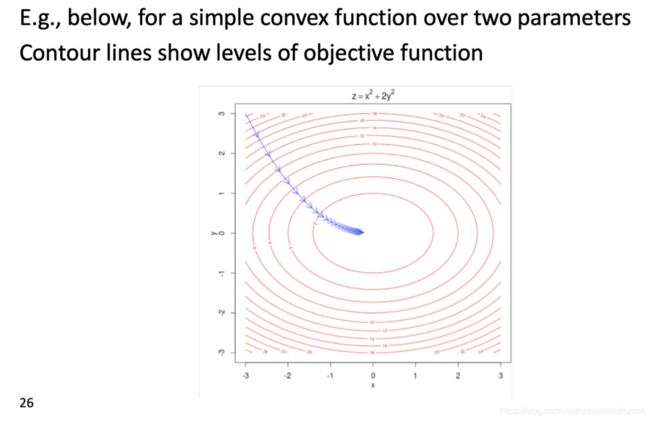
5. Optimization basics
Optimization:Gradient Descent(梯度下降)
-
我们的损失函数 J ( θ ) J(\theta) J(θ) 需要最小化
-
使用的方法为:梯度下降
-
对于当前 θ \theta θ ,计算 J ( θ ) J(\theta) J(θ) 的梯度
-
然后小步重复朝着负梯度方向更新方程里的参数 α = ( s t e p s i z e ) o r ( l e a r n i n g r a t e ) \alpha=(step\ size)\ or\ (learning\ rate) α=(step size) or (learning rate)
θ n e w = θ o l d − α ∇ θ J ( θ ) \theta^{new}=\theta^{old}-\alpha \nabla_\theta J(\theta) θnew=θold−α∇θJ(θ) -
更新唯一的参数 θ \theta θ:
θ j n e w = θ j o l d − α α α θ j o l d J ( θ ) \theta_j^{new}=\theta_j^{old}-\alpha \frac \alpha{\alpha\ \theta_j^{old}}J(\theta) θjnew=θjold−αα θjoldαJ(θ)
while True:
theta_grad = evaluate_gradient(J,corpus,theta)
theta = theta - alpha * theta_grad
SGD:Stochastic Gradient Descent
-
由于 J ( θ ) J(\theta) J(θ) 是在语料文本中所有窗口的方程
-
当语料很大的时候,计算梯度会消耗巨大
-
解决办法:SGD
-
不断sample窗口,不断更新
while True: window = sample_window(corpus) theta_grad = evaluate_gradient(J,window,theta) theta = tehta - alpha * theta_grad
参考资料
- CS224n 课程主页
- CS224n 中英视频