【数据结构与算法Python描述】——栈的Python实现及其简单应用

【数据结构与算法Python描述】——Python列表实现原理深入探究及其常用操作时间复杂度分析主要介绍了Python內置数据结构list的底层原理，从本文开始，我们将学习建构在list上的数据结构栈、队列和双端队列。

从本文开始，我们在学习不同的数据结构时都将遵循下列步骤：

• 先分析其功能原型；
• 然后给出其功能的抽象描述；
• 最后使用Python实现。

其中，为了能够以一种统一的方式来对待实现数据结构的功能进行抽象描述，这里先引入所谓抽象数据类型（ADT：Abstract Data Types）的概念（一下简称ADT）：

ADT是对于某一数据结构所支持的功能的抽象描述，该描述指定了可以对该数据结构执行何种操作、执行操作时接收和返回何种参数。ADT仅明确该数据结构所支持的操作是“做什么”，而并不涉及“怎么做”。

一、栈

1. 栈的定义

栈是保存了一组对象元素的集合，该集合在插入和删除元素时遵循后进先出的原则。

2. 栈的原型

如果要使用一个实际生活中的案例来说明什么是栈的话，其原型所下图所示的糖果机，即：

• 一端封闭，一端开口；
• 放入糖果时，最先放入的糖果在最下方，最后放入的糖果在最上方；
• 取出糖果时，最上面的糖果（即最后放入）最先被取出。

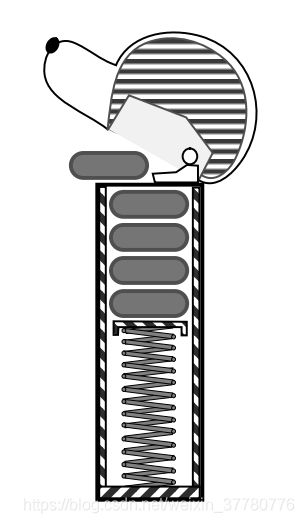
实际上，上述糖果机的封闭端压缩了一根弹簧，所以放入糖果时的操作是“压入”，取出糖果时的操作是“弹出”。

3. 栈的ADT

基于上述讨论，我们知道一个栈实例的ADT至少包含下列两个方法：

• stack.push(e)：将元素e压入栈stack的顶部；
• stack.pop()：弹出栈stack的顶部元素并将其返回，如果此时栈为空，则抛出异常。

实际上，为了更好的使用栈，一般还需要定义下列方法：

• stack.top()：仅返回栈stack顶部元素而不删除，如果栈为空则抛出异常；
• stack.is_empty()：如果栈stack为空，则返回True；
• __len__()：重写该方法使得可以使用len(stack)来返回栈的深度，即元素数量。

4. 栈的实现

要想实现栈，则必须要能保存元素，自然地，可以使用Python的列表list。list类中，已经支持：

• 使用append()方法向其尾部追加一个元素；
• 使用pop()方法删除尾部最后一个元素。

因此，很自然地，将栈的顶部和列表的尾部对齐，那么对于列表的append()和pop()操作就相当于是栈的push()和pop()操作。

但是，如果仅按照上述方式来实现栈是不够的，原因在于list中还包含从任意位置删除元素的方法，这将会破坏栈的ADT。因此，我们考虑仅在栈的内部使用list的实例来存储元素，然后借由list已有操作元素的方法来实现栈的ADT，且屏蔽list类的所有其他方法。

4.1 适配器设计模式

实际上，上述描述体现了编程中的一种程序设计思想——适配器设计模式（Adapter Design Pattern），这种编程思想适用于任何当我们不希望或不能修改其源码的情况下修改一个已知类的行为的情况。

如果你曾去过和国内电压不一样的国家，你可能买过充电器的转换器，这实际上就是适配器设计模式的一种现实体现。

通常在编程中使用面向对象程序设计范式来应用适配器设计模式的通用方法是：

• 首先定义一个新的类，并且将已有类的一个实例作为新类的私有属性；
• 然后使用上述私有属性的方法来实现新类的各个方法。

基于上述讨论，使用Python中的list来实现栈时，栈的方法和列表相关方法的对应关系如下：

栈的方法	基于的列表方法
stack.push(e)	lst.append(e)
stack.pop()	lst.pop()
stack.top()	lst[-1]
stack.is_empty()	len(lst) == 0
len(stack)	len(lst)

4.2 使用列表实现栈

在使用列表实现栈类Stack之前，需要考虑的另外一个问题是，本文在栈的ADT中要求当栈为空时，stack.top()和stack.pop()操作均抛出异常，但仍需要确定的是具体应该为哪种异常。实际上，当列表为空时，调用其pop()方法会抛出IndexError异常，但对于栈来说并不存在所谓索引的概念，对此我们可以考虑自定义一个名称更加合理的异常类型：

class Empty(Exception):
    """尝试对空栈执行pop()或top()操作时抛出的异常"""
    pass

基于上述讨论，下面给出了基于list实现栈Stack的完整代码，其中__init__()方法中的私有属性self._data是一个初始为空的列表，用作存储栈中元素用：

class Empty(Exception):
    """尝试对空栈执行pop()或top()操作时抛出的异常"""
    pass


class Stack:
    """使用Python列表作元素存储用实现的栈数据结构类，元素存取遵循后进先出原则"""

    def __init__(self):
        """栈初始化为空"""
        self._data = list()

    def __len__(self):
        """
        返回栈中元素个数
        :return: int 栈中元素个数，也叫栈的深度
        """
        return len(self._data)

    def __str__(self):
        """
        以无歧义的方式返回栈的字符串表示形式
        :return: 底层列表的字符串表示形式
        """
        return str(self._data)

    def is_empty(self):
        """
        如果栈为空，则返回True
        :return: Boolean 栈是否为空
        """
        return len(self._data) == 0

    def push(self, element):
        """
        将对象索引以元素形式压入栈顶
        :param element: 待压入栈顶的对应索引
        :return: None
        """
        self._data.append(element)

    def top(self):
        """
        返回但不删除栈的元素，如栈为空则抛出Empty异常
        :return: 栈顶元素
        """
        if self.is_empty():
            raise Empty("栈为空！")
        return self._data[-1]  # 以索引-1的方式获取列表最后一个元素

    def pop(self):
        """
        删除并返回栈顶元素，如栈为空则抛出Empty异常
        :return: 栈顶元素
        """
        if self.is_empty():
            raise Empty("栈为空！")
        return self._data.pop()  # 使用列表的pop()方法删除最后一个元素


def main():
    stack = Stack()
    stack.push(5)
    stack.push(3)
    print(stack)  # 输出为[5, 3]
    print(len(stack))  # 输出为：2
    print(stack.pop())  # 输出为：3
    print(stack.is_empty())  # 输出为：False
    print(stack.pop())  # 输出为：5
    print(stack.is_empty())  # 输出为：True


if __name__ == '__main__':
    main()

4.3 栈操作复杂度分析

下表列出了上述Stack类各方法的时间复杂度，鉴于其基于list类实现，因此根据文章数据结构与算法Python描述】——Python列表实现原理深入探究及其常用操作时间复杂度分析中的分析:

• 对于Stack的top()、is_empty()以及len()方法，其最坏时间复杂度均为$O(1)$;
• 对于Stack的push()和pop()方法，鉴于其使用list类的append()和pop()方法实现，因此其经摊销后的时间复杂度也为$O(1)$。

操作	时间复杂度
stack.push(e)	$O(1)$1
stack.pop()	$O(1)$1
stack.top()	$O(1)$
stack.is_empty()	$O(1)$
len(stack)	$O(1)$

5. 栈的应用

栈是数据结构中最基础的一种，但其在实际代码中应用也十分广泛，例如：

• 浏览器的后退功能：用户使用浏览器时，每从当前页面通过超链接跳转至另一个页面时，当前页面的网址就会被压入栈顶，后续当用户点击“后退”时，就会将栈顶的网站地址依次弹出。
• 文本编辑器的撤销功能：同理，文本编辑器也会将用户所作的每一次操作压入栈顶，当用户点击撤销时实现操作回退。

此处鉴于篇幅无法实现栈的上述两种较为复杂应用，而只是给出两种较为简单的应用：

5.1 匹配括号

在数学表达式中，一般可能会包含下列三类括号：

• 小括号：'('和')'；
• 大括号：'{'和'}'；
• 中括号：'['和']'

每一个类型的左半括号都必须有一个对应的右半括号与之相匹配，除此之外，各类型括号之间的相对顺序也有要求，下列给出了几种正确和错误的匹配方式：

• 正确：()(()){([()])}
• 正确：((()(()){([()])}))
• 错误：)(()){([()])}
• 错误：({[])}
• 错误：(

下列是判断诸如数学表达式[(5+x)-(y+z)]中的括号匹配是否合法的代码：

from array_stack import Stack  # 上述实现Stack的代码保存在名为array_stack.py的文件中


def is_matched(expr):
    """
    判断数学表达式expr中的各类括号是否正确成对匹配，如果是返回True，否则返回False
    :param expr: 数学表达式
    :return: Boolean
    """
    lefty = '({['  # 括号类型的左半部分
    righty = ')}]'  # 括号类型的右半部分
    stack = Stack()
    for c in expr:
        if c in lefty:
            stack.push(c)  # 将括号类型左半部分压栈
        elif c in righty:  # 只要上一个if条件和该elif条件任意一个为真，下面的两个if条件都将会被判断
            if stack.is_empty():
                return False  # 无可匹配的括号
            if righty.index(c) != lefty.index(stack.pop()):
                return False
    return stack.is_empty()

假设上述函数的输入参数expr为'[(5+x)-(y+z)]'，那么程序执行的过程大致为，当程序从左至右扫描字符串的每个字符时：

• 每次程序遇到某一左半括号时，程序将该符号压入栈stack的顶部；
• 每次程序遇到一个右半括号时，程序从栈stack的顶部弹出一个元素（假设此时栈非空），并将二者进行比较，判断二者是否可正确配对；
• 如果程序扫描完所有expr中的字符后，stack为空，则必定所有的括号都正确地进行了配对，反之，必定有左半括号无对应类型的右半括号与之配对。

5.2 匹配标签

下面是一段以HTML写的源代码，要求判断是否每一个标签都正确得到了匹配。

<body>
<center>
<h1> The Little Boat h1>
center>
<p> The storm tossed the little boat like a cheap sneaker in an old washing machine. The three drunken fishermen were used to such treatment, of course, but not the tree salesman, who even as a stowaway now felt that he had overpaid for the voyage. p>
<ol>
<li> Will the salesman die? li>
<li> What color is the boat? li>
<li> And what about Naomi? li>
ol>
body>

下列是使用上述Stack实现的匹配判断算法：

from array_stack import Stack  # 上述实现Stack的代码保存在名为array_stack.py的文件中


def is_matched_html(raw_html: str):
    """
    如果所有的HTML标签都正确配对则返回True，否则返回False
    :param raw_html: 字符串形式的原始HTML文本
    :return: Boolean
    """
    stack = Stack()
    j = raw_html.find('<')  # 查找可能存在的第一个'<'字符
    while j != -1:
        k = raw_html.find('>', j + 1)  # 查找下一个'>'字符
        if k == -1:
            return False  # 非法格式标签
        tag = raw_html[j + 1: k]  # 去除标签的'<'和'>'
        if not tag.startswith('/'):  # 判断是否为左半标签
            stack.push(tag)
        else:  # 此为右半标签
            if stack.is_empty():
                return False  # 无可与右半标签匹配的左半标签
            if tag[1:] != stack.pop():
                return False  # 标签匹配错误（成对的标签只能嵌套，不能交叉）
        j = raw_html.find('<', k + 1)  # 查找下一个可能存在的'<'字符
    return stack.is_empty()  # 判断是否完成对所有标签的尝试匹配

与栈十分类似的另一种数据结构是队列，关于这种数据结构的介绍请见文章【数据结构与算法Python描述】——队列和双端队列。

---

1. 摊销时间复杂度。 ↩︎ ↩︎