第七题 螺旋矩阵(模拟题)
问题描述
对于一个nn 行 mm 列的表格,我们可以使用螺旋的方式给表格依次填上正整数,我们称填好的表格为一个螺旋矩阵。
例如,一个 44 行 55 列的螺旋矩阵如下:
1 2 3 4 5
14 15 16 17 6
13 20 19 18 7
12 11 10 9 8
输入格式
输入的第一行包含两个整数 n, mn,m,分别表示螺旋矩阵的行数和列数。
第二行包含两个整数 r, cr,c,表示要求的行号和列号。
输出格式
输出一个整数,表示螺旋矩阵中第 rr 行第 cc 列的元素的值。
样例输入
4 5
2 2
样例输出
15
评测用例规模与约定
对于 30% 的评测用例,2 <= n, m <= 20。
对于 70% 的评测用例,2 <= n, m <= 100。
对于所有评测用例,2 <= n, m <= 1000,1 <= r <= n,1 <= c <= m。
思路:
创建一个二维螺旋矩阵找对应点。 QAQ 没有什么算法思想 就简简单单老老实实创建矩阵叭
python代码实现 (小洪四个循环丑陋版)
import sys
n, m = map(int,input().split())
r, c = map(int,input().split())
chess = [[0 for i in range(m)] for j in range(n)]
num = 1
t = 0
while True:
for i in range(t,m-t):
chess[t][i] = num
num += 1
if num == n*m+1 or t == r-1 and i == c-1:
print(chess[r-1][c-1])
sys.exit(0)
for j in range(t+1,n-t):
chess[j][m-t-1] = num
num += 1
if num == n*m+1 or j == r-1 and m-t-1 == c-1:
print(chess[r-1][c-1])
sys.exit(0)
for k in range(i-1,t-1,-1):
chess[n-1-t][k] = num
num += 1
if num == n*m+1 or n-1-t == r-1 and k == c-1:
print(chess[r-1][c-1])
sys.exit(0)
for l in range(j-1,t,-1):
chess[l][t] = num
num += 1
if num == n*m+1 or l == r-1 and t == c-1 :
print(chess[r-1][c-1])
sys.exit(0)
t += 1第八题 摆动序列 (DP)
Problem Description
如果一个序列的奇数项都比前一项大,偶数项都比前一项小,则称为一个摆动序列。
即 $a_{2i} < a_{2i-1}, a_{2i+1} > a_{2i}$
小明想知道,长度为 m,每个数都是 1 到 n 之间的正整数的摆动序列一共有多少个。
Input && Output
输入一行包含两个整数 m,n。
输出一个整数,表示答案。答案可能很大,请输出答案除以10000的余数。
Sample Input && Output
Inout
3 4
Output
14
Ideas
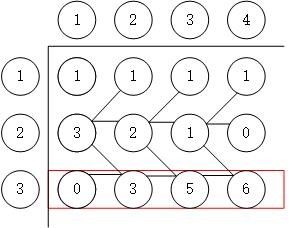
挺好的一道基础dp,po一张图解释一下测试用例是怎么出来的你们就懂了
从后往前推比较好推,
dp[i][j]讨论倒数第i位数字是j的时候,有几种情况。
第一层数组全为1,后面每一层根据层数的奇&偶分别求上一层的前缀&后缀和,最后一层的和即为所求
# 状态转移方程 分奇&偶
arr[i][j] = arr[i][j + 1] + arr[i + 1][j + 1]
arr[i][j] = arr[i][j - 1] + arr[i + 1][j - 1]记得时刻处理一下求余,python虽然不存在爆int问题,但是会MLE(血的教训QAQ)
Code
if __name__ == "__main__":
m, n = map(int, input().split())
arr = [[0 for i in range(n + 2)] for j in range(m + 1)]
for i in range(1, n + 1):
arr[m][i] = 1
for i in range(m - 1, 0, -1):
if i % 2 == 0:
for j in range(n, 0, -1):
arr[i][j] = (arr[i][j + 1] + arr[i + 1][j + 1]) % 10000
else:
for j in range(1, n + 1):
arr[i][j] = (arr[i][j - 1] + arr[i + 1][j - 1]) % 10000
ans = 0
for i in range(1, n + 1):
ans += arr[1][i] % 10000
print(ans % 10000)第九题 村庄建设(最小生成树)
问题描述
2015年,全中国实现了户户通电。作为一名电力建设者,小明正在帮助一带一路上的国家通电。
这一次,小明要帮助 n 个村庄通电,其中 1 号村庄正好可以建立一个发电站,所发的电足够所有村庄使用。
现在,这 n 个村庄之间都没有电线相连,小明主要要做的是架设电线连接这些村庄,使得所有村庄都直接或间接的与发电站相通。
小明测量了所有村庄的位置(坐标)和高度,如果要连接两个村庄,小明需要花费两个村庄之间的坐标距离加上高度差的平方,形式化描述为坐标为 (x_1, y_1) 高度为 h_1 的村庄与坐标为 (x_2, y_2) 高度为 h_2 的村庄之间连接的费用为
sqrt((x_1-x_2)(x_1-x_2)+(y_1-y_2)(y_1-y_2))+(h_1-h_2)*(h_1-h_2)。
在上式中 sqrt 表示取括号内的平方根。请注意括号的位置,高度的计算方式与横纵坐标的计算方式不同。
由于经费有限,请帮助小明计算他至少要花费多少费用才能使这 n 个村庄都通电。
输入格式
输入的第一行包含一个整数 n ,表示村庄的数量。
接下来 n 行,每个三个整数 x, y, h,分别表示一个村庄的横、纵坐标和高度,其中第一个村庄可以建立发电站。
输出格式
输出一行,包含一个实数,四舍五入保留 2 位小数,表示答案。
样例输入
4
1 1 3
9 9 7
8 8 6
4 5 4
样例输出
17.41
评测用例规模与约定
对于 30% 的评测用例,1 <= n <= 10;
对于 60% 的评测用例,1 <= n <= 100;
对于所有评测用例,1 <= n <= 1000,0 <= x, y, h <= 10000。
解法一:Kruskal算法 (贪心+并查集)
思路:
(1) 从最小边权的边开始,按边权从小到大依次加入,如果某次加边产生了环,就扔掉这条边,直到加入了n-1条边,即形成了一棵树。
(2) 开一个列表inf[ ],按各边代价从小到大排序存储信息。例:(point1,point2,cost)
(3) 循环判断此边是否与树连通,若连通,放弃此边;若不连通,将此边与树相连,记录相应代价。
(4) 连通判断方法:采用并查集算法,开一个列表fa[ ],下标为子节点,对应存储其父节点。例:fa[2]=1 节点2的父节点为1
(5) 此题可直接用fa[ ]列表存储各点的祖先节点,相同祖先节点的点说明其在同一颗树下。
python代码实现
import math
def find(x):
if x != fa[x]:
fa[x] = find(fa[x])
return fa[x]
def unionset(x,y):
x = find(x)
y = find(y)
if x == y:
return
fa[y] = x
n = int(input())
point = []
inf = []
fa = [i for i in range(n+1)]
ans = 0
for i in range(n):
point.append(list(map(int,input().split())))
for i in range(n):
for j in range(i+1,n):
point1 = i+1
point2 = j+1
cost = math.sqrt((point[i][0]-point[j][0])**2+(point[i][1]-point[j][1])**2)+(point[i][2]-point[j][2])**2
inf.append((point1,point2,cost))
inf = sorted(inf,key = lambda x:x[2])
for i in range(len(inf)):
if find(inf[i][0]) != find(inf[i][1]):
ans += inf[i][2]
unionset(inf[i][0],inf[i][1])
print('%.2f'%ans)第十题 郊外植树 (DFS)
问题描述
小明和朋友们一起去郊外植树,他们带了一些在自己实验室精心研究出的小树苗。
小明和朋友们一共有 nn 个人,他们经过精心挑选,在一块空地上每个人挑选了一个适合植树的位置,总共 nn个。他们准备把自己带的树苗都植下去。
然而,他们遇到了一个困难:有的树苗比较大,而有的位置挨太近,导致两棵树植下去后会撞在一起。
他们将树看成一个圆,圆心在他们找的位置上。如果两棵树对应的圆相交,这两棵树就不适合同时植下(相切不受影响),称为两棵树冲突。
小明和朋友们决定先合计合计,只将其中的一部分树植下去,保证没有互相冲突的树。他们同时希望这些树所能覆盖的面积和(圆面积和)最大。
输入格式
输入的第一行包含一个整数 nn ,表示人数,即准备植树的位置数。
接下来 nn行,每行三个整数 x, y, rx,y,r,表示一棵树在空地上的横、纵坐标和半径。
输出格式
输出一行包含一个整数,表示在不冲突下可以植树的面积和。由于每棵树的面积都是圆周率的整数倍,请输出答案除以圆周率后的值(应当是一个整数)。
样例输入
6
1 1 2
1 4 2
1 7 2
4 1 2
4 4 2
4 7 2
样例输出
12
评测用例规模与约定
对于 30% 的评测用例,1 <= n <= 10;
对于 60% 的评测用例,1 <= n <= 20;
对于所有评测用例,1 <= n <= 30,0 <= x, y <= 1000,1 <= r <= 1000。
思路:
这是一道经典的搜索问题,遍历不同的种树组合,找出面积最大的组合即可。
(1) 爆搜一般都是用递归完成,每次递归选取一个可行解,若找到可行解,继续下一层递归;无可行解,回溯上一层递归。
(2) 在递归中,为了减少不必要的搜索浪费,我们需要开几个标签进行判断。
tree[ ] 记录已经种下的树组合 v[i] 记录第几课树是否种下
(3) 变量idx记录种树次数,变量i记录树的标号。
(4) 此题小技巧:当idx种树次数与n棵树相同时,即取得最大种树组合,可直接结束递归。
python代码实现
import math
import sys
def dfs(idx):
global ans
global ans1
for i in range(n):
if not v[i]:
if not tree:
tree.append(i)
v[i] = True
ans += inf[i][2]**2
dfs(idx+1)
v[i] = False
ans -= inf[i][2]**2
tree.remove(tree[-1])
else:
flag = 1
for j in tree:
l = math.sqrt((inf[i][0]-inf[j][0])**2+(inf[i][1]-inf[j][1])**2)
if l < inf[i][2]+inf[j][2]:
flag = 0
if flag:
tree.append(i)
v[i] = True
ans += inf[i][2]**2
dfs(idx+1)
v[i] = False
ans -= inf[i][2]**2
tree.remove(tree[-1])
if ans >= ans1:
ans1 = ans
if idx == n-1:
print(ans1)
sys.exit(0)
return
n = int(input())
inf = []
tree = []
ans = 0
ans1 = 0
v = [False for i in range(n)]
for i in range(n):
inf.append(list(map(int,input().split())))
dfs(0)
print(ans1)