剑指offfer 51-67 C++

51.构建乘积数组

给 定 一 个 数 组 A[0,1,…,n-1], 请 构 建 一 个 数 组 B[0,1,…,n-1], 其中B中的元素

B[i]=A[0]A[1]…A[i-1]A[i+1]…A[n-1]。不能使用除法。

//B[i]其实就是等于 A 中除 A[i]之外的所有元素之积。
//从左到右算 B[i]=A[0]*A[1]*...*A[i-1],            从右到左算B[i]*=A[i+1]*...*A[n-1]
//而 C[i]和 D[i]的递推公式： C[i]=C[i-1]*A[i-1]       D[i]=D[i+1]*A[i+1]
//可以通过数组 A 从前往后得到 C，从后往前得到 D；然后通过 C 和 D 得到 A。

//初始化vector正三角的时候元素全入，然后反三角的时候每个元素重新计算
class Solution { 
public: 
    vector<int> multiply(const vector<int>& A) { 
        vector<int> ret; 
        int size = A.size(); 
        ret.push_back(1); //先入一个1
        for(int i=0;i<size-1;i++) ret.push_back(ret.back()*A[i]);//push的是[1,size-1]
        int tmp = 1;
        for(int i=size-1;i>=0;i--){ //计算的是[size-1,0],下标在这个范围内的数值需要改变
            ret[i] *= tmp; 
            tmp *= A[i]; 
        }
        return ret; 
    } 
};
//O(n)时间：分成前后两部分。
//前半部分：B[i]=B[i-1]*A[i-1]； 后半部分：反向遍历，利用tmp累乘A[i],B[i]*=tmp;
class Solution {
public:
    vector<int> multiply(const vector<int>& A) {   
        int n=A.size();
        vector<int> b(n);
        int ret=1;
        for(int i=0;i<n;ret*=A[i++])     b[i]=ret;//这里正三角的乘积，计算完保存到b[i]
        ret=1;
        for(int i=n-1;i>=0;ret*=A[i--])  b[i]*=ret;//每一项的b[i]再*对应反三角的ret
        return b;
    }
};

52.正则表达式匹配

请实现一个函数用来匹配包括’.‘和’‘的正则表达式。模式中的字符’.‘表示任意一个字符，而’’ 表示它前面的字符可以出现任意次（包含 0 次）。 在本题中，匹配是指字符串的所有字符 匹配整个模式。例如，字符串"aaa"与模式"a.a"和"ab* ac* a"匹配，但是与"aa.a"和"ab*a"均 不匹配

//要分为几种情况：（状态机）
//（1）当第二个字符不为‘*’时：匹配就是将字符串和模式的指针都下移一个，不匹配就直接返回false
//（2）当第二个字符为'*'时：
//  匹配：
//    a.字符串下移一个，模式不动(匹配一个)
//    b.同a(匹配多个可以是相同情况，因为：当匹配一个时，由于str移到了下一个字符，而pattern字符不变，回
//      到了上边的情况)

//    c.字符串不动，模式下移两个(匹配0个)
//  不匹配：
//    字符串下移不动，模式下移两个(匹配0个)
class Solution {
public:
    bool match(char* str, char* pattern)
    {
        if (*str == '\0' && *pattern == '\0') return true;
        if (*str != '\0' && *pattern == '\0') return false;
        if (*(pattern+1) != '*')
        {
            if (*str == *pattern || (*str != '\0' && *pattern == '.'))  
                return match(++str, ++pattern);
            else return false;
        }
        else
        {//当它的下一个是 星星,,
            if (*str == *pattern || (*str != '\0' && *pattern == '.'))  
               return match(str, pattern+2) || match(++str, pattern);
            //匹配情况下的str不动，pat+2：
            //aaa和aa＊aa，a＊就相当于消了，主串不往后移，继续和模式往后移的字符匹配
            else return match(str, pattern+2);
            //aa和ab＊a，b＊就相当于消了，主串不往后移
        }
    }
};

53.表示数值的字符串

请实现一个函数用来判断字符串是否表示数值（包括整数和小数）。

例如，字符串 “+100”,“5e2”,"-123",“3.1416"和”-1E-16"都表示数值。

但是"12e",“1a3.14”,“1.2.3”,"±5"和 "12e+4.3"都不是。

//常规解法
class Solution {
public:
bool isNumeric(char* str)
{ // 标记符号、小数点、e是否出现过
    bool sign = false, decimal = false, hasE = false;
    for (int i = 0; i < strlen(str); i++) {
        if (str[i] == 'e' || str[i] == 'E') { 		
            if (i == strlen(str) - 1||i==0) return false; // e不能位于首位和末尾
            if (str[i - 1] == '.') return false;  //e不能直接接在.后面一位
            if (hasE) return false;  // 不能同时存在两个e
            hasE = true;
        }
        else if (str[i] == '+' || str[i] == '-') {
            // 第二次出现+-符号，则必须紧接在e之后
            if (sign && str[i - 1] != 'e' && str[i - 1] != 'E') return false;
            // 第一次出现+-符号，且不是在字符串开头，则也必须紧接在e之后
            if (!sign && i > 0 &&str[i - 1] != 'e'&&str[i - 1] != 'E') return false;
            sign = true;
        }
        else if (str[i] == '.') {
            // e后面不能接小数点，小数点不能出现两次
            if (hasE || decimal) return false;
            decimal = true;
        }
        else if (str[i] < '0' || str[i] > '9') // 不合法字符
            return false;
    }
    return true;
}
};
//状态迁移表
class Solution {
public:
    char arr[10] = "+-n.ne+-n";
    int turn[10][9] = {
       //+  -  n  .  n  e  +  -  n
        {1, 1, 1, 0, 0, 0, 0, 0, 0},    // # start
        {0, 0, 1, 1, 0, 0, 0, 0, 0},    // +
        {0, 0, 1, 1, 0, 0, 0, 0, 0},    // -
        {0, 0, 1, 1, 0, 1, 0, 0, 0},    // n
        {0, 0, 0, 0, 1, 0, 0, 0, 0},    // .
        {0, 0, 0, 0, 1, 1, 0, 0, 0},    // n
        {0, 0, 0, 0, 0, 0, 1, 1, 1},    // e
        {0, 0, 0, 0, 0, 0, 0, 0, 1},    // +
        {0, 0, 0, 0, 0, 0, 0, 0, 1},    // -
        {0, 0, 0, 0, 0, 0, 0, 0, 1}     // n
    };
    bool isNumeric(char* string) {
        int cur = 0;
        for(int j, i = 0; string[i]; i++) {
            for(j = 0; j < 9; j++) {
                if(turn[cur][j]) {
                    if(('0' <= string[i] && string[i] <= '9' && arr[j] == 'n') ||
                        (string[i] == 'E' && arr[j] == 'e')||
                        string[i] == arr[j]) {
                        cur = j + 1;
                        break;
                    }
                }
            }
            if(j == 9) return false;
        }
        if(cur == 3 || cur == 4 || cur == 5 || cur == 9)
           return true;
        return false;
    }
};
//自动机
class Solution {
public:
    bool isNumeric(char* string)
    {
        int j，i=0;
        while(j != 6){
            switch(j){
                case 0:
                    if( string[i]== '-' || string[i] == '+' || isdigit(string[i]) ) j=1;
                    else return false;
                    break;
                case 1:
                    if(isdigit(string[i])) j=1;
                    else if(string[i] == '.') j=2;
                         else if(string[i] == '\0') j=6;
                              else if(string[i] == 'e' || string[i] == 'E') j=4;
                                    else return false;
                    break;
                case 2:
                    if( isdigit(string[i])) j=3;
                    else return false;
                    break;
                case 3:
                    if( isdigit(string[i]) ) j=3;
                    else if(string[i] == 'e' || string[i] == 'E') j=4;
                         else if( string[i] == '\0') j=6;
                              else return false;
                    break;
                case 4:
                    if( isdigit(string[i]) || string[i] == '+' || string[i] == '-') j=5;
                    else return false;
                    break;
                case 5:
                    if( isdigit(string[i])) j=5;
                    else if( string[i] == '\0') j=6;
                         else  return false;
                    break;
            }
            i++;
        }
        return true;
    }
};

54.字符流中第一个不重复的字符

请实现一个函数用来找出字符流中第一个只出现一次的字符。例如，当从字符流中只读出前 两个符"go"时，第一个只出现一次的字符是"g"。当从该字符流中读出前六个字符“google" 时，第一个只出现一次的字符是"l"。

class Solution
{
public:
    //仿照hash表实现，str存储插入的字符，hash[256]存储插入字符的个数
    string str;
    char hash[256] = {0};//char占一个字节（8位），无符号范围为0~255
    void Insert(char ch)
    {
        str += ch;//把输入的这个字符存入字符串
        hash[ch]++;//每存入一个就+1，先计算完再重新遍历
    }
    //遍历插入的字符（按照插入的顺序，可方便的得到第一个），hash表中个数为1的输出，否则返回#
    char FirstAppearingOnce()
    {//遍历的是每个字符
        for(auto ch : str) if(hash[ch] == 1)  return ch;
        return '#';
    }
};

55.链表中环的入口结点

给一个链表，若其中包含环，请找出该链表的环的入口结点，否则，输出null。

//断链法   破坏链表结构   时间复杂度为O（n）
//用slow和fast2个指针，一前一后，一起往后走，访问过的结点都断开，最后快的会走到尾结点的next跳出循环。慢的刚好就在入环口
class Solution {
public:
    ListNode* EntryNodeOfLoop(ListNode* pHead)
    {
        if(!pHead || !pHead->next) return nullptr;//只有1结点也不可能有环
        ListNode* slow = pHead;
        ListNode* fast = pHead->next;
        while(fast){//出口是fast不为空
            slow->next=NULL;//断开
            slow = fast;
            fast = fast->next;
        }
        if(!slow && !fast) return nullptr;//没有环的时候
        return slow;
    }
};
//HashSet 遍历List的同时用Set来存储每一个节点，如果链表有环的话，一定会把相同的节点存进去，那么这就说入口。  时间复杂度为O（n）
public ListNode EntryNodeOfLoop1(ListNode pHead){
    Set<ListNode>set=new HashSet<>();
    while (pHead!=null){
        if(set.contains(pHead))return pHead;
        else set.add(pHead);
        pHead=pHead.next;
    }
    return null;
}
//使用快慢指针
//结论1、设置快慢指针，假如有环，他们最后一定相遇。
//结论2、两个指针分别从链表头和相遇点继续出发，每次走一步，最后一定相遇与环入口。
//证明结论1：设置快慢指针fast和low，fast每次走两步，low每次走一步。假如有环，两者一定会相遇
//(慢指针肯定没走完一圈就被快的追上) 
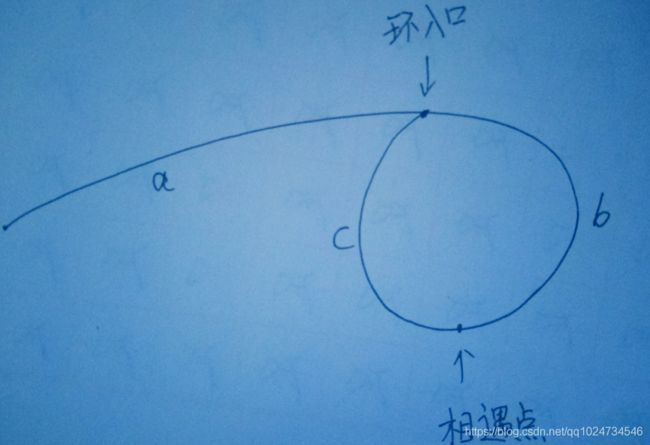
//证明结论2：
//链表头到环入口长度为--a
//环入口到相遇点长度为--b
//相遇点到环入口长度为--c
//则：相遇时快指针路程=a+(b+c)k+b ，k>=1  其中b+c为环的长度，k为绕环的圈数（k>=1,即最少一圈，不能是0圈，不然和慢指针走的一样长，矛盾）。
//慢指针路程=a+b 
//快指针走的路程是慢指针的两倍，所以： （a+b）*2=a+(b+c)k+b
//化简可得：  a=(k-1)(b+c)+c 这个式子的意思是： 链表头到环入口的距离=相遇点到环入口的距离+（k-1）圈环长度。其中k>=1,所以k-1>=0圈。所以两个指针分别从链表头和相遇点出发，最后一定相遇于环入口。
class Solution {
public:
    ListNode* EntryNodeOfLoop(ListNode* pHead)
    {
        ListNode* fast=pHead,* slow=pHead;//一起走
        while(fast && fast->next){//保证每个结点但不为空
            fast=fast->next->next;//fast一下走两步
            slow=slow->next;//slow走一步
            if(fast==slow) break;//有环必相遇
        }
        if(!fast || !fast->next) return null;//无环
        slow=pHead;//slow从链表头部出发
        while(fast!=slow){//fast从相遇点出发
            fast=fast->next;
            slow=slow->next;
        }
        return slow;
    }
};

56.删除链表中重复的结点

在一个排序的链表中，存在重复的结点，请删除该链表中重复的结点，重复的结点不保留， 返回链表头指针。 例如，链表 1->2->3->3->4->4->5 处理后为 1->2->5

//每次递归：删除当前指针向后的连续节点。保证下一次递归的头结点与之后的不重复；找到下一个不重复的节点与其相连
class Solution {
public:
    ListNode* deleteDuplication(ListNode* pHead)
    {
        if (!pHead || !pHead->next) return pHead;//0/1个结点直接返回头，也是递归出口，NULL的话结束
        ListNode* cur;
        if ( pHead->next->val==pHead->val){//当前结点等于下一个
            cur=pHead->next;//cur指向下一个
            while (cur->next && cur->next->val==pHead->val)//有下一个且还想等
                cur=cur->next;//走到相等的最后一个，此节点和前面的还是相等的
            return deleteDuplication(cur->next);//递归往后第一个不相等的，NULL的话结束             
        }
        else {//此节点和下个不相等
            cur=pHead->next;//下个结点递归过去
            pHead->next=deleteDuplication(cur);//重构链表
            return pHead;//每次返回的都是头
        }    
    }
};
//双指针+标识符
class Solution {
public:
    ListNode* deleteDuplication(ListNode* pHead)
    {
        if (!pHead) return pHead;
        ListNode *pre = NULL;
        ListNode *cur = pHead;
        bool flag = 0;//默认为0,无重复数字
        while (cur)
        {//有下个结点且和当前结点相等
            while (cur->next && cur->next->val == cur->val)
            {
                cur = cur->next;//走到最后一个相等结点
                flag = 1;
            }
            if (flag)//还在走重复结点
            {
                if (!pre) pHead = cur->next;//要换头的情况，换到cur->next
                else pre->next = cur->next;//头换完了 pre指向cur->next
                flag = 0;
            }
            else pre = cur;//flag为0 要换pre了，pre总是是cur的前面位置
            cur = cur->next;
        }
        return pHead;
    }
}

57.二叉树的下一个结点

给定一个二叉树和其中的一个结点，请找出中序遍历顺序的下一个结点并且返回。注意，树 中的结点不仅包含左右子结点，同时包含指向父结点的指针。

//1.二叉树为空，则返回空；
//2.节点右孩子存在，则下一个是右子树最左边的结点；
//3.前提是节点不是根节点。如果该节点是其父节点的左孩子，则返回父节点；
//如果是右孩子，继续向上遍历其父节点的父节点，重复之前的判断，返回结果。
class Solution {
public:
    TreeLinkNode* GetNext(TreeLinkNode* pNode)
    {
        if(pNode==NULL) return NULL;
        if(pNode->right!=NULL)
        {
            pNode=pNode->right;
            while(pNode->left!=NULL) pNode=pNode->left;
            return pNode;
        }  
        while(pNode->next!=NULL)
        {
            TreeLinkNode *proot=pNode->next;
            if(proot->left==pNode) return proot;
            pNode=pNode->next;
        }
        return NULL;
    }
};

58.对称的二叉树

请实现一个函数，用来判断一颗二叉树是不是对称的。注意，如果一个二叉树同此二叉树的镜像是同样的，定义其为对称的。

//迭代1  
class Solution {
public:
    bool isSymmetrical(TreeNode* pRoot)
    {
        if(!pRoot) return true;
        queue<TreeNode*> q1,q2;
        TreeNode *left,*right;
        q1.push(pRoot->left);
        q2.push(pRoot->right);
        while(!q1.empty() && !q2.empty()){
            left = q1.front();
            q1.pop();
            right = q2.front();
            q2.pop(); //要注意访问到空节点的情况，和下面的2个判定不可以混淆
            if(!left && !right) continue;//2个都是空，可能访问到空节点,跳出循环继续
            if(!left || !right) return false;//两边都有节点
            if(left->val != right->val) return false;//2个节点的值相等
            q1.push(left->left);
            q1.push(left->right);
            q2.push(right->right);
            q2.push(right->left);
        }
    return true;
    }
};
//递归1
class Solution {
public:
    bool isSymmetrical(TreeNode* pRoot)
    {
        return isSame(pRoot,pRoot);
    }
    bool isSame(TreeNode* l, TreeNode* r) {
        if(l && r && l->val==r->val)
            return isSame(l->left,r->right) && isSame(l->right,r->left);
        return !l && !r;//当不相等 一个为空的时候返回0，当2个都为空的时候返回1
    }
};
//递归2  如果先序遍历的顺序分为两种先左后右和先右后左两种顺序遍历，如果两者相等说明二叉树是对称的二叉树
class Solution {
public:
    bool isSame(TreeNode* p1,TreeNode* p2)
    {
        if(!p1 && p2) return false;
        if(!p2 && p1) return false;
        if(!p1 || !p2) return true;
        if(p1->val == p2->val) 
            return isSame(p1->left,p2->right) && isSame(p1->right,p2->left);
        else return false;
    }
    bool isSymmetrical(TreeNode* pRoot)
    {
        if(!pRoot) return true;
        return isSame(pRoot->left,pRoot->right);
    }
};

59.按之字形顺序打印二叉树

请实现一个函数按照之字形打印二叉树，即第一行按照从左到右的顺序打印，第二层按照从 右至左的顺序打印，第三行按照从左到右的顺序打印，其他行以此类推。

class Solution {
public:
    vector<vector<int> > Print(TreeNode* pRoot) {
        vector<vector<int> > result;//结果
        stack<TreeNode *> stack1,stack2;//双栈
        if(pRoot) stack1.push(pRoot);//入根节点
        while(!stack1.empty() || !stack2.empty()){
            vector<int> data;//存放每层的节点
            TreeNode *node;//一层里面存放的节点
            if(!stack1.empty()){//stack1不为空
                while(!stack1.empty()){
                    node = stack1.top();
                    stack1.pop();
                    data.push_back(node->val);//保存奇数行数据
                    if(node->left) stack2.push(node->left);//入栈出栈在头，不用逆置遍历顺序
                    if(node->right) stack2.push(node->right);
                }
            }
            else if(!stack2.empty()){
                while(!stack2.empty()){
                    node = stack2.top();
                    stack2.pop();
                    data.push_back(node->val);//保存偶数行数据
                    if(node->right) stack1.push(node->right);//在这里需要逆置遍历顺序
                    if(node->left)  stack1.push(node->left);
                }
            }
            result.push_back(data);
        }
        return result;
    }
};

60.把二叉树打印成多行

从上到下按层打印二叉树，同一层结点从左至右输出。每一层输出一行。

//用单队列
class Solution {
public:
    vector<vector<int> > Print(TreeNode* pRoot) {
        vector<vector<int> > result;//结果
        queue<TreeNode*> que;//用队列存放每层的元素
        if(pRoot) que.push(pRoot);//先入头
        while(!que.empty()){
            vector<int> tmp;
            int n = que.size();
            while(n--){
                TreeNode* node = que.front();
                que.pop();
                tmp.push_back(node->val);
                if(node->left) que.push(node->left);//node用来存放下一层的结点
                if(node->right) que.push(node->right);
                
            }
            result.push_back(tmp);
        }
        return result;
    }
};
//双队列 双vector
class Solution {
public:
        vector<vector<int> > Print(TreeNode* pRoot) {
            vector<vector<int>> ret;
            queue<TreeNode*> q1, q2;
            if(pRoot) q1.push(pRoot);
            while(!q1.empty() || !q2.empty()){
                vector<int> v1,v2;
                while(!q1.empty()){
                    v1.push_back(q1.front()->val);
                    if(q1.front()->left) q2.push(q1.front()->left);
                    if(q1.front()->right) q2.push(q1.front()->right);
                    q1.pop();
                }
                if(v1.size()!=0) ret.push_back(v1);
                while(!q2.empty()){
                    v2.push_back(q2.front()->val);
                    if(q2.front()->left)   q1.push(q2.front()->left);
                    if(q2.front()->right)  q1.push(q2.front()->right);
                    q2.pop();
                }
                if(v2.size()!=0) ret.push_back(v2);
            }
            return ret;
        }  
};

61.序列化二叉树

请实现两个函数，分别用来序列化和反序列化二叉树

二叉树的序列化是指：把一棵二叉树按照某种遍历方式的结果以某种格式保存为字符串，从而使得内存中建立起来的二叉树可以持久保存。序列化可以基于先序、中序、后序、层序的二叉树遍历方式来进行修改，序列化的结果是一个字符串，序列化时通过 某种符号表示空节点（#），以 ！ 表示一个结点值的结束（value!）。二叉树的反序列化是指：根据某种遍历顺序得到的序列化字符串结果str，重构二叉树。

//vector
//1.序列化：二叉树被记录成文件的过程叫作二叉树的序列化
//借助整型类型的vector数组存储二叉树节点值，所以进行序列化的时候，对二叉树进行前序遍历将节点加入数组，当节点为空的时候，加入特殊数值0xFFFFFFF，并退出递归。由于函数需要返回字符数组类型，因此还需要将vector数组中的元素一一复制到动态整型数组中，最后对整型数组强制转换为字符类型。
//2：反序列化：通过文件内容重建原来的二叉树过程叫做二叉树反序列化
//先将字符数组类型转为整型数组，然后二叉树的节点的值就可以直接从整型数组中得到。首先，处理递归出口，如果遇到0xFFFFFFF，则指针向后移动一个单位并退出递归，否则构造二叉树根节点，并继续移动指针，连接递归得到的左子树以及右子树。
class Solution {
public:
    vector<int> buf;
    void SerHelper(TreeNode *p){//前序遍历
    if(!p)  buf.push_back(0xFFFFFFF);//标记空节点
        else{
            buf.push_back(p->val);
            SerHelper(p->left);
            SerHelper(p->right);
        }
    }
    char* Serialize(TreeNode *root) {//复制buf中的元素并转为字符型
        SerHelper(root);//前序遍历存入buf
        int *stream=new int[buf.size()];//把buf里面的元素拷过来
        for(int i=0;i<buf.size();i++) stream[i]=buf[i];
        return (char*)stream;//强制类型转换
    }
   
   TreeNode* Deserialize(char *str) {
       int *p=(int*)str;//强制类型转换
       return DeserHelper(p);
    }
    TreeNode* DeserHelper(int*& p){//注意此处需要加引用
        if(*p==0xFFFFFFF){
            ++p;
            return nullptr;
        }
        TreeNode *root=new TreeNode(*p);
        ++p;
        root->left=DeserHelper(p);//递归构造左子树并连接到根节点的左孩子
        root->right=DeserHelper(p);//递归构造右子树并连接到根节点的右孩子
        return root;
    }
};
//使用stringstream
//1.借助string类型的变量来拼接序列化的字符串。只需前序遍历二叉树，当遇到根节点为空时，追加 ‘#’，并退出递归，否则追加二叉树的根节点值，接着追加逗号。接下只需递归实现左子树和右子树的序列化。那么，序列化之后得到了string类型的字符串，最后构造动态字符数组，将字符串的每一个字符复制到字符数组中，结尾加入’\0’标记结束。
//2.进行反序列化时，如果遇到 ‘#’ ，那么指针移动一个单位，退出递归。否则，找到字符数组中的一个二叉树节点值，然后构造根节点，如果此时到达字符末尾，直接返回根节点，否则指针继续移动一个单位。接下来根节点的左右指针分别连接左子树的递归实现结果和右子树的递归实现结果。
class Solution {
public:   
    char* Serialize(TreeNode *root)
    {
        string s = sHelper(root);
        char *ret = new char[s.length() + 1];
        strcpy(ret, const_cast<char*>(s.c_str()));
        return ret;
    }
        string sHelper(TreeNode *node)
    {
        if (!node) return "#";
        return to_string(node->val) + "," +
                sHelper(node->left) + "," + sHelper(node->right);
    }
    
    
     TreeNode* Deserialize(char *str) {
        stringstream ss(str);
        return dHelper(ss);
    }
 
    TreeNode *dHelper(stringstream &ss)
    {
        string str;
        getline(ss, str, ',');
        if (str == "#")
            return NULL;
        else
        {
            TreeNode *node = new TreeNode(stoi(str));
            node->left = dHelper(ss);
            node->right = dHelper(ss);
            return node;
        }
    }
};
//atoi()和stoi()
相同点：
//1.都是C++的字符处理函数，把数字字符串转换成int输出
//2.头文件都是#include 
不同点：
//1.atoi()的参数是 const char* ,因此对于一个字符串str我们必须调用 c_str()的方法把这个string转换成 const char*类型的,而stoi()的参数是const string*,不需要转化为 const char*；
//2.stoi()会做范围检查，默认范围是在int的范围内的，如果超出范围的话则会runtime error！
//而atoi()不会做范围检查，如果超出范围的话，超出上界，则输出上界，超出下界，则输出下界；

62.二叉搜索树的第 k 个结点

给定一棵二叉搜索树，请找出其中的第k小的结点。例如， （5，3，7，2，4，6，8） 中，按结点数值大小顺序第三小结点的值为4。

//递归 
//采用递归的方式，不断递归深入根节点的左孩子，直到碰到空节点为止，然后回溯输出当前节点。再以同样的方式递归遍历其右孩子。在此期间，每访问一个节点，我们都对k进行减一操作，直到k为0，说明该节点即为第k个节点。
class Solution {
public:
    int m;
    TreeNode* ans;
    void dfs(TreeNode* p){
        if(!p || m < 1) return;//不满足条件直接返回NULL/每次递归出口：
        dfs(p -> left);//走到了最左边结点,到空不继续递归，该节点左右走完了回溯上一层
        if(m == 1) ans = p;//最左边结点 / m-到1的时候，当前结点就是第m小
        if(--m > 0) dfs(p -> right);// 右子树同样处理/遍历该节点的右节点 (左中右)
    }
    TreeNode* KthNode(TreeNode* p, unsigned int k){
        ans = NULL; m = k;//初始化 ans=NULL 不满足条件返回NULL
        dfs(p);
        return ans; 
    }
};
//非递归   死扣递归很多时候还是有必要的，它不仅是一种优美的思路，简洁的代码，更体现的是对函数不断调入与回溯这一过程的整体把握，基于整个递归程序流程的理解再去写非递归会更简单。递归的过程其实就是函数不断的调入，在计算机中每一个函数都是一个栈帧，函数的调入与完成对应入栈与出栈。
//非递归版中序遍历，可以利用栈来模拟递归遍历，首先根入栈，然后令根节点的左孩子不断入栈直到为空，弹出栈顶，令其右孩子入栈，重复以上操作，直到遍历结束或者访问第k个节点为止。
class Solution {
public:
    TreeNode* KthNode(TreeNode* pRoot, int k)
    {
        if(!pRoot) return nullptr;
        stack<TreeNode*> res;
        TreeNode* p = pRoot;
        while(!res.empty() || p){//栈为空 and p指向NULL 就跳出循环
            while(p){//当前节点p不是NULL，才会入栈，且遍历左
                res.push(p);
                p = p->left;//先走到最左边节点的下个左，是NULL，但不入
            }
            TreeNode* node = res.top();//保存且遍历这个结点的右，遍历完此节点回溯上一个左边结点
            res.pop();//出去，遍历它的右
            if((--k) == 0) return node;//结果判定
            p = node->right;//左-->中-->右
        }
        return nullptr;
    }
};

63.数据流中的中位数

如何得到一个数据流中的中位数？如果从数据流中读出奇数个数值，那么中位数就是所有数 值排序之后位于中间的数值。如果从数据流中读出偶数个数值，那么中位数就是所有数值排 序之后中间两个数的平均值。

堆的参考 ： 我是链接

//读入每个数后，从小到大排序，取中值即可。时间复杂度为 O(nlogn)
class Solution { 
public: 
    vector<int> data; 
    void Insert(int num){ 
        data.push_back(num); 
    }
    double GetMedian() { 
        int size = data.size(); 
        sort(data.begin(),data.end()); 
        if(size & 1) return data[size >> 1];//size是奇数
        else return (data[(size-1) >> 1]+data[size >> 1])/2.0; 
    } 
};
//用一个大顶堆和一个小顶堆，维持大顶堆的数都小于等于小顶堆的数，且两者的个数相等或差1。平均数就在两个堆顶的数之中。
class Solution {
//右边小顶堆的元素都大于左边大顶堆的元素，并且左边元素的个数，要么与右边相等（偶数次输入），要么比右边大1（奇数次输入）
    priority_queue<int, vector<int>, less<int> > p; // 大顶堆    
    priority_queue<int, vector<int>, greater<int> > q;// 小顶堆  从小到大
public:
    void Insert(int num){
        if(p.empty() || num <= p.top()) p.push(num);
        else q.push(num);
        // 左边大顶堆的大小最多可以比右边小顶堆大1（奇数次输入）
        if(p.size() == q.size() + 2) q.push(p.top()), p.pop();
        // 因为最后返回的只有可能是左边大顶堆的堆顶，所以右边小顶堆的大小不能比左边小顶堆大
        if(p.size() + 1 == q.size()) p.push(q.top()), q.pop();
    }
    double GetMedian(){ 
      return p.size() == q.size() ? (p.top() + q.top()) / 2.0 : p.top();
    }
};
//堆其实就是利用完全二叉树的结构来维护的一维数组
//priority_queue是（优先队列）是一个封装好的堆结构
//priority_queue默认为大顶堆，即堆顶元素为堆中最大元素。

64.滑动窗口的最大值

给定一个数组和滑动窗口的大小，找出所有滑动窗口里数值的最大值。例如，如果输入数组{2,3,4,2,6,2,5,1}及滑动窗口的大小3，那么一共存在6个滑动窗口，他们的最大值分别为{4,4,6,6,6,5}； 针对数组{2,3,4,2,6,2,5,1}的滑动窗口有以下6个： {[2,3,4],2,6,2,5,1}， {2,[3,4,2],6,2,5,1}， {2,3,[4,2,6],2,5,1}， {2,3,4,[2,6,2],5,1}， {2,3,4,2,[6,2,5],1}， {2,3,4,2,6,[2,5,1]}。

class Solution {52
public:
    vector<int> maxInWindows(const vector<int>& num, unsigned int size)
    {
        vector<int> res;
        deque<int> s;//存num的下标
        for(unsigned int i=0;i<num.size();++i){
            while(s.size() && num[s.back()]<=num[i])
 //从后面依次弹出队列中比当前num值小的元素，同时也能保证队列首元素为当前窗口最大值下标
 //为了保证队首最大，所以从队尾开始一个个比较，如果当前值num[i]比队尾大，此时的队尾的数就弹出，然后继续比较队尾是否比当前值num[i]大.
                s.pop_back();
            while(s.size() && i-s.front()+1>size)
                //当当前窗口移出队首元素所在的位置，即队首元素坐标对应的num不在窗口中，需要弹出
                s.pop_front();
            s.push_back(i);//把每次滑动的num下标加入队列
            if(size&&i+1>=size)//当滑动窗口首地址i大于等于size时才开始写入窗口最大值
                res.push_back(num[s.front()]);
        }
        return res;
    }
};

65.矩阵中的路径

请设计一个函数，用来判断在一个矩阵中是否存在一条包含某字符串所有字符的路径。路径可以从矩阵中的任意一个格子开始，每一步可以在矩阵中向左，向右，向上，向下移动一个格子。如果一条路径经过了矩阵中的某一个格子，则该路径不能再进入该格子。 例如 a b c e s f c s a d e e 矩阵中包含一条字符串"bcced"的路径，但是矩阵中不包含"abcb"路径，因为字符串的第一个字符b占据了矩阵中的第一行第二个格子之后，路径不能再次进入该格子。

;//回溯算法
//这是一个可以用回溯法解决的典型题。首先，在矩阵中任选一个格子作为路径的起点。如果路径上的第i个字符不是ch，那么这个格子不可能处在路径上的第i个位置。如果路径上的第i个字符正好是ch，那么往相邻的格子寻找路径上的第i+1个字符。除在矩阵边界上的格子之外，其他格子都有4个相邻的格子。重复这个过程直到路径上的所有字符都在矩阵中找到相应的位置。
//由于回溯法的递归特性，路径可以被开成一个栈。当在矩阵中定位了路径中前n个字符的位置之后，在与第n个字符对应的格子的周围都没有找到第n+1个字符，这个时候只要在路径上回到第n-1个字符，重新定位第n个字符。
//由于路径不能重复进入矩阵的格子，还需要定义和字符矩阵大小一样的布尔值矩阵，用来标识路径是否已经进入每个格子。 当矩阵中坐标为（row,col）的格子和路径字符串中相应的字符一样时，从4个相邻的格子(row,col-1),(row-1,col),(row,col+1)以及(row+1,col)中去定位路径字符串中下一个字符；
//如果4个相邻的格子都没有匹配字符串中下一个的字符，表明当前路径字符串中字符在矩阵中的定位不正确，我们需要回到前一个，然后重新定位。
//一直重复这个过程，直到路径字符串上所有字符都在矩阵中找到合适的位置
class Solution {
public:
    bool hasPath(char* matrix, int rows, int cols, char* str)
    {  
      if(!str||rows<=0||cols<=0) return false;
      bool *isOk=new bool[rows*cols]();
      for(int i=0;i<rows;i++)
      {
           for(int j=0;j<cols;j++)
                if(isHsaPath(matrix,rows,cols,str,isOk,i,j)) return true;
      }
      return false;
    }
 bool isHsaPath(char *matrix,int rows,int cols,char *str,bool *isOk,int curx,int cury)
 {
//题目中的矩阵是用一维数组来表示二维数组的，所以要针对行列情况进行处理，curx表示当前第几行，cury表示某一行上的第几个元素，当cury = -1时，说明该行起点前面一个元素，所以要退回到上一行末尾的那个元素;当cury = cols说明是处于改行末尾一点的下一个点，所以前进到下一行的起点。仔细想想，其实题目的意思是上一行末尾的点可以和下一行的起始的点连接起来，所以需要这样处理
      if(*str=='\0') return true;
      if(curx<0||curx>=rows||cury<0||cury>=cols) return false;
      if(isOk[curx*cols+cury]||*str!=matrix[curx*cols+cury]) return false;
      isOk[curx*cols+cury]=true;
      bool sign=isHsaPath(matrix,rows,cols,str+1,isOk,curx-1,cury)
       ||isHsaPath(matrix,rows,cols,str+1,isOk,curx+1,cury)
       ||isHsaPath(matrix,rows,cols,str+1,isOk,curx,cury-1)
       ||isHsaPath(matrix,rows,cols,str+1,isOk,curx,cury+1);
      isOk[curx*cols+cury]=false;
      return sign;
 }
};  

66.机器人的运动范围

地上有一个 m 行和 n 列的方格。一个机器人从坐标 0,0 的格子开始移动，每一次只能向左， 右，上，下四个方向移动一格，但是不能进入行坐标和列坐标的数位之和大于 k 的格子。 例 如，当 k 为 18 时，机器人能够进入方格（35,37），因为 3+5+3+7 = 18。但是，它不能进 入方格（35,38），因为 3+5+3+8 = 19。请问该机器人能够达到多少个格子？

class Solution {
public:
    int movingCount(int threshold, int rows, int cols)
    {
        bool* flag=new bool[rows*cols];
        for(int i=0;i<rows*cols;i++) flag[i]=false;
        int count=moving(threshold,rows,cols,0,0,flag);//从（0,0）坐标开始访问;
        delete[] flag;
        return count;
    }
    //计算最大移动位置
    int moving(int threshold,int rows,int cols,int i,int j,bool* flag)
    {
        int count=0;
        if(check(threshold,rows,cols,i,j,flag))
        {
            flag[i*cols+j]=true;
            //标记访问过，这个标志flag不需要回溯，因为只要被访问过即可。
           //因为如果能访问，访问过会加1.不能访问，也会标记下访问过。
            count=1+moving(threshold,rows,cols,i-1,j,flag)
                   +moving(threshold,rows,cols,i,j-1,flag)
                   +moving(threshold,rows,cols,i+1,j,flag)
                   +moving(threshold,rows,cols,i,j+1,flag);
        }
        return count;
    }
    //检查当前位置是否可以访问
    bool check(int threshold,int rows,int cols,int i,int j,bool* flag)
    {
        if(i>=0 && i<rows && j>=0 && j<cols
            && getSum(i)+getSum(j)<=threshold
            && flag[i*cols+j]==false)
           return true;
        return false;
    }
    //计算位置的数值
    int getSum(int number)
    {
        int sum=0;
        while(number>0) sum+=number%10,number/=10;
        return sum;
    }
};

67.剪绳子

给你一根长度为n的绳子，请把绳子剪成m段（m、n都是整数，n>1并且m>1），每段绳子的长度记为k[0],k[1],…,k[m]。请问k[0]xk[1]x…xk[m]可能的最大乘积是多少？例如，当绳子的长度是8时，我们把它剪成长度分别为2、3、3的三段，此时得到的最大乘积是18。

//动态规划
class Solution {
public:
    int cutRope(int number) {
        if(number<2) return 0;
        if(number==2) return 1;
        if(number==3) return 2;
        int *res = new int[number+1];//res存放剪完剩下长度的最大积
        res[0]=0; res[1]=1; res[2]=2; res[3]=3;
        int max = 0;
        for(int i=4;i<=number;++i){
            max = 0;
            for(int j=1;j<=i/2;++j){
                int num = res[j]*res[i-j];
                if(max < num) max =num;
                res[i] = max;
            }
        }
        max = res[number];
        delete[] res;
        return max;
    }
};
//贪婪算法：当n大于等于5时，我们尽可能多的剪长度为3的绳子；当剩下的绳子长度为4时，把绳子剪成两段长度为2的绳子。 为什么选2，3为最小的子问题？因为2，3包含于各个问题中，如果再往下剪得话，乘积就会变小。 为什么选长度为3？因为当n≥5时，3(n−3)≥2(n−2)
class Solution {
public:
    int cutRope(int number) {
    if (number < 2) return 0;
    if (number == 2) return 1;
    if (number == 3) return 2;
    int time3 = number/3;
        //剩下4
    if(number - time3*3 == 1) time3--;
        int time2 =(number - time3*3)/2;
        return (int)(pow(3,time3)) * (int)(pow(2,time2));
    }
};