数据结构C语言 Part1 引入篇

什么是数据结构呢？没有官方定义，不过数据结构+算法==程序。而很好的Data Structure（本学期以后简称DS）可以带来最优效率的算法。解决问题的效率，和数据的组织方式、空间的利用效率以及算法的巧妙程度有关。应该说，算法和数据结构都很重要。按学校的安排，我们先学DS再学Algorithm。我们先看几个例子引入一下：

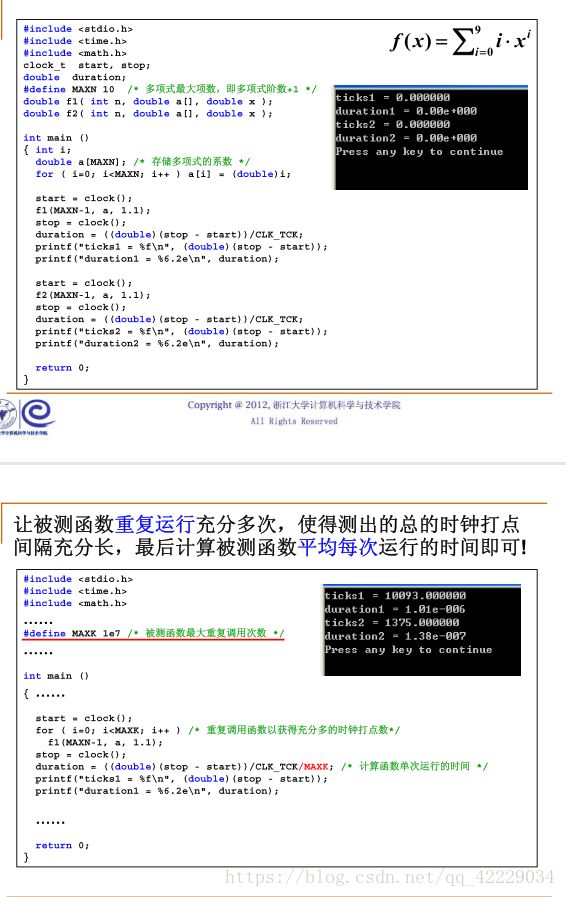
例子一：写程序计算给定多项式在某一个给定的点的值：

介绍与一些知识储备：

#include 
#include 

//这个多项式是f(x)=a0+a1x+a2x^2+...+an*x^n

//我们用最直接的想法来计算：
double f1(int n,double a[],double x) //我们要尽可能避免浮点数和整型的四则运算
{
    int i；
    double p=a[0];  //a[i] represents the value of i(th) term in sequence
    for(i=1;i<=n;i++)
        p+=a[i-1]+x*p;
    return p;
}


//当n足够大了，我们看得出来这个计算量还是很大的，不如我们改进一下算法：
double f2(int n,double a[],double x)
{
    int i;
    double p=a[n];
    for(i=n;i>0;i--)
        p=a[i-1]+x*p;
    return p;
}

//这个思路是基于f(x)=a0+x(a1+x(...(an-1 + x(an))...))

/*接下来我们再介绍一下clock()这个函数,这个函数是捕捉从程序开始运行 到clock()被调用所消耗时间，这个时间单位时clock tick，即“时钟打点”。常数CLOCKS_PER_SEC代表机器时钟每秒走过的时钟打点数,即1000ms*/

clock_t start,stop; //clock_t 时clock（）函数返回的变量类型
double duration; //记录被测函数的运行时间

int main()
{
    start=clock();
    function();               //这里代表一个抽象的函数模块，你懂我的意思吧
    stop=clock();
    duration =((double)(stop-start))/CLOCKS_PER_SEC; //计算function的运行时间
    exit(0);   //啊哈，题外话，exit是退出当前进程，return只是退出当前的函数
}

这里我们简化一下问题，就是求f（x）=x+2x^2+...+n*x^n在x=1.1处的值f（1.1），按顺序结构编写代码，如下：

我们再谈谈ADT--抽象数据类型：

一、数据类型：数据对象集与 数据集合相关联的操作集

二、抽象：描述数据类型的方法不依赖于具体实现，于存放数据的机器无关，与数据存储的物理结构无关，与实现操作的算法和编程语言无关。也就是说，我们只关注数据对象集和操作集是什么，而不关注其如何做到的实现机理。

三、ADT={D，S，P}，是数据对象、关系、操作集合的三元组。

在严蔚敏的教材中，有一些约定俗称，我们这里举出一点来：

1.数据元素，我们用ElemType来表示

2.形参表中，用C++传引用的方式，即“&”来表示引用参数地址

3.内存的动态申请和释放，我们用指针变量 = new 数据类型； ... ;  delete 指针变量。

。。。。etc

我们举一个综合一点的例子来看看：

你譬如说：矩阵，的抽象数据类型定义，我们可以给出如下的定义：

类型名称：矩阵（Matrix）

数据对象集：一个m×n的矩阵Am×n=（aij），其中i从1到m，j从1到n，由m*n哥三元组（a，i，j）构成，a代表这个位置元素的大小，i，j代表行号和列号。

操作集：对于任意矩阵...和整数...,有：

Matrix Create(int M,int N);//返回一个M*N的空矩阵

int GetMaxRow（Matrix A）；//返回A的总行数

Matrix Add（Matrix A，Matrix B）;//如果A，B可加，则返回他们的和矩阵，否则返回错误提示信息

...（etc）。

我们接下来看看算法，第一章都是很浅的东西，这个我们瞅瞅浙大的ppt就好。今天上课了，顺便补一点我的笔记：

笔记：

算法是为了实现某个目标的有穷指令集，描述算法有自然语言（但是有二义性（就是不太容易口头上说清楚），不太推荐，朋友之间吹逼当然可以），流程图，北邮限定NS图，程序设计语言（代码）和Pseudo code伪代码（嗯，算法导论...）来表示。算法的特性是正确性、可读性（别人能够看得懂，这也是防止你被co-worker砍死的重要的一点），健壮性（不能你来个错误输入系统就崩了吧），高效性（我们用时间复杂度和空间复杂度来衡量）。

对于时间复杂度，我们分为事后复杂度（当你程序跑完，计 算 掐 表跑了多久，这个和计算机的系统，编译环境有关，对真实算法优劣的衡量是不好的，我们已经淘汰了这种分析法了）和事前复杂度分析。事前复杂度分析就是根据算法本身执行次数来衡量，只和算法本身有关。至于时间复杂度的定义，大家心里都有b数，我们不废话了。再谈谈优化算法，优化算法并不是你这次花了三分钟跑出结果，下次花了2分钟就叫优化了。学术上，我们认为优化算法是降低了算法的时间复杂度的阶。比如我下面所提到的，用O（n^3）的规模，用在线处理的方式，优化到O（n）的规模，这才是真正的优化了算法。

for(i=1;i<=n;i++)                            //频度n
    for(j=1;j<=n;j++)                        //频度n*n
    {
        c[i][j]=0;
        for(k=1;k<=n;k++)
        c[i][j]=c[i][j]+a[i][k]*b[k][j];     //频度为n^3

    }
//这是矩阵的乘法(Cij=A的第i行*B的第j列)，可见他是n^3的scale

可见，算法需要的时间规模是需要我们比较严格把控的，比如当基数比较大，我们就不推荐用选择排序，而用快速排序等更好的排序方式。

另外在分析复杂度的时候，别的我们不说了，if-else结构的复杂度取决于if的条件判断复杂度和两个分支部分的复杂度，总体复杂度取三者中最大者。

接下来我们应用一下我们前面所学的知识，来解决一个最大子列和的问题，顺便再看我的代码的时候，想想复杂度该是多少。

应用实例：最大连续子列和问题（进一步可以引申到背包问题）。

给定N个整数的序列{A1,A2,A3。。。An}

求函数f（i，j）=max{0，Σ Ak}，其中求和符号下界是k=i，上界是j

在这里我们提供四种算法，复杂度不同。

//算法一
int MaxSubsequenceSum1(int A[],int N)
{
    int ThisSum,MaxSum=0;
    int i,j,k;
    for(i=0;iMaxSum)
            MaxSum=ThisSum;       //若得到的子列和更大，就更新MaxSum结果
        }
    }
    return MaxSum;
}

这个思路是最直接的思路，由于i，j的位置不确定性，所以我们需要先后遍历i、j，再对i到j位号的元素求和，来求出这样一个sum。可见，这个思路的时间复杂度是T(N)=O(N^3).

//算法二
int MaxSubsequenceSum2(int A[],int N)
{
    int ThisSum,MaxSum=0;
    int i,j;
    for(i=0;iMaxSum)
            MaxSum=ThisSum;
        }
    }
    return MaxSum;
}

这个思路是在第一个思路上进行的改编，算法复杂度是T（N）=O（N^2）.

算法三：分治法，虽然暂时不是很懂，算法复杂度是O（NlogN）

int Max3( int A, int B, int C ) 
{
 /* 返回3个整数中的最大值 */   
  return A > B ? A > C ? A : C : B > C ? B : C; 
} 


int DivideAndConquer( int List[], int left, int right ) 
{ 
/* 分治法求List[left]到List[right]的最大子列和 */    
 int MaxLeftSum, MaxRightSum; /* 存放左右子问题的解 */    
 int MaxLeftBorderSum, MaxRightBorderSum; /*存放跨分界线的结果*/  
   int LeftBorderSum, RightBorderSum;  
   int center, i;   
   if( left == right ) 
   { /* 递归的终止条件，子列只有1个数字 */    
     if( List[left] > 0 )
     return List[left];   
     else return 0;    
   }   
  /* 下面是"分"的过程 */   
  center = ( left + right ) / 2; 
  /* 找到中分点 */  
   /* 递归求得两边子列的最大和 */     
   MaxLeftSum = DivideAndConquer( List, left, center );   
  MaxRightSum = DivideAndConquer( List, center+1, right );   
  /* 下面求跨分界线的最大子列和 */  
   MaxLeftBorderSum = 0;
 LeftBorderSum = 0;   
  for( i=center; i>=left; i-- ) 
  { 
  /* 从中线向左扫描 */       
  LeftBorderSum += List[i];       
  if( LeftBorderSum > MaxLeftBorderSum )         
    MaxLeftBorderSum = LeftBorderSum;    
  }
 /* 左边扫描结束 */   
  MaxRightBorderSum = 0;
  RightBorderSum = 0;  
   for( i=center+1; i<=right; i++ ) 
   { /* 从中线向右扫描 */      
   RightBorderSum += List[i];       
  if( RightBorderSum > MaxRightBorderSum )      
       MaxRightBorderSum = RightBorderSum;    
   } 
  /* 右边扫描结束 */   
  /* 下面返回"治"的结果 */    
 return Max3( MaxLeftSum, MaxRightSum, MaxLeftBorderSum + MaxRightBorderSum );
 } 
int MaxSubseqSum3( int List[], int N ) { /* 保持与前2种算法相同的函数接口 */    
 return DivideAndConquer( List, 0, N-1 ); }

//算法四：在线处理
int MaxSubsequenceSum4(int A[],int N)
{
    int ThisSum,MaxSum;
    int i;
    ThisSum=MaxSum=0;
    for(i=0;iMaxSum)    
            MaxSum=ThisSum;   //发现更大的子列和就更新当前结果
        else if(ThisSum<0)    //如果当前子列和为负
            ThisSum=0;        //就不可能使后面的部分和增大，抛弃之
    }
    return MaxSum;
}

 

T(N)=O(N),在线的意思是指每输入一个数据都能得到即时处理，在任何一个地方中止输入，算法都能正确给出当前的答案。一般来说，效率如此之高，会带来副作用，这个副作用，就是...不太容易理解。不过，当你举个例子，就能懂为什么要这么写了。这个算法的核心思想是，当前面的子列和为负数，我们就把它清零，抛弃不要，从后面重新开始，因为对于最优解而言，前面的不可能再提供积极的作用，只可能提供消极的作用。这个思路我也是今天才见到，觉得很巧妙，因为不论如何你把这个序列看一遍，复杂度都是N，而这个算法竟然可以控制复杂度在O（N），理解机理之后，真的很妙，发现了编程之美。

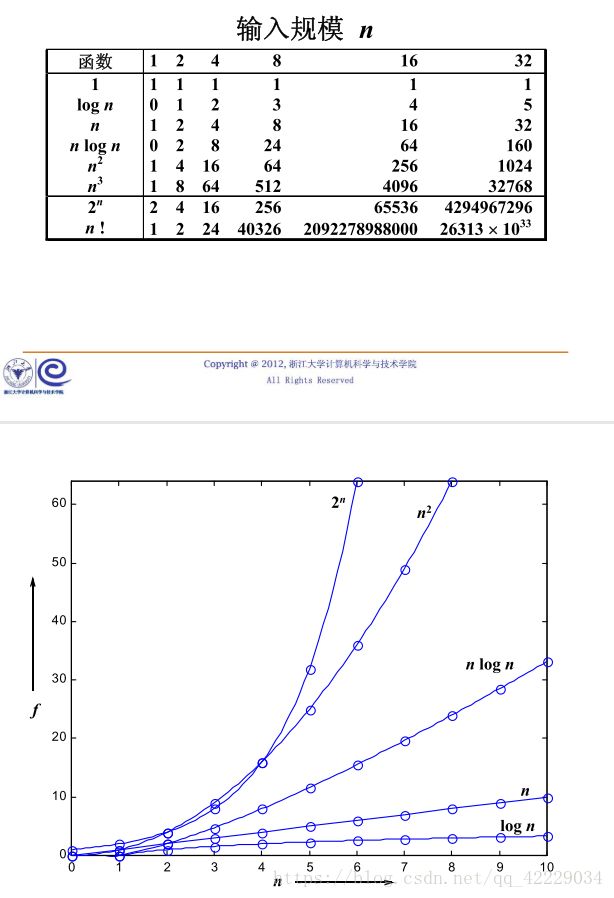
我们给出了以上四种算法，可见输入规模较大的时候，前两个算法就吃不消了。

我们在数据结构作的铺垫就到这里了，国庆节假期也正式完结了，明天第一堂课就是数电、数据结构，我也要加油鸭！

这几天我会做一个ADT的表示与实现的伪码表示（在下次DS课前）。//坑已经补好了

线性表、链表的知识我们随后再讲吧。（本周内完成）

等我周末忙完了，就把课后题的一些luminous point总结在这里吧。