Selective Search原理及实现
在目标检测时,为了定位到目标的具体位置,通常会把图像分成许多子块,然后把子块作为输入,送到目标识别的模型中。分子块的最直接方法叫滑动窗口法。滑动窗口的方法就是按照子块的大小在整幅图像上穷举所有子图像块。这种方法产生的数据量想想都头大。和滑动窗口法相对的是另外一类基于区域(region proposal)的方法。selective search就是其中之一!
首先通过简单的区域划分算法,将图片划分成很多小区域,再通过相似度和区域大小(小的区域先聚合,这样是防止大的区域不断的聚合小区域,导致层次关系不完全)不断的聚合相邻小区域,类似于聚类的思路。这样就能解决object层次问题。
最后对于计算速度来说,只能说这个思路在相对穷举,大大减少了后期分类过程中的计算量。
算法流程:

step0:生成区域集R,具体参见论文《Efficient Graph-Based Image Segmentation》
step1:计算区域集R里每个相邻区域的相似度S={s1,s2,…}
step2:找出相似度最高的两个区域,将其合并为新集,添加进R
step3:从S中移除所有与step2中有关的子集
step4:计算新集与所有子集的相似度
step5:跳至step2,直至S为空
为了保证能够划分的完全,对于相似度,作者提出了可以多样化的思路,不但使用多样的颜色空间(RGB,Lab,HSV等等),还有很多不同的相似度计算方法。
- 颜色空间变换:将原始色彩空间转换到多达八中的色彩空间。然后通过多样性的距离计算方式,综合颜色、纹理等所有的特征。
- 距离计算方式需要满足两个条件,其一速度得快啊,因为毕竟我们这么多的区域建议还有这么多的多样性。其二是合并后的特征要好计算,因为我们通过贪心算法合并区域,如果每次都需要重新计算距离,这个计算量就大太多了。
1.颜色距离就是对各个通道计算颜色直方图,然后取各个对应bins的直方图最小值。这样做的话两个区域合并后的直方图也很好计算,直接通过直方图大小加权区域大小然后除以总区域大小就好了。

2.纹理距离计算方式和颜色距离几乎一样,我们计算每个区域的快速sift特征,其中方向个数为8,3个通道,每个通道bins为10,对于每幅图像得到240维的纹理直方图

3.优先合并小的区域,如果仅仅是通过颜色和纹理特征合并的话,很容易使得合并后的区域不断吞并周围的区域,后果就是多尺度只应用在了那个局部,而不是全局的多尺度。因此我们给小的区域更多的权重,这样保证在图像每个位置都是多尺度的在合并。
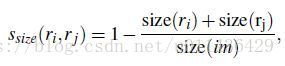
4.区域的合适度度距离,不仅要考虑每个区域特征的吻合程度,区域的吻合度也是重要的,吻合度的意思是合并后的区域要尽量规范,不能合并后出现断崖的区域,这样明显不符合常识,体现出来就是区域的外接矩形的重合面积要大。因此区域的合适度距离定义为:

5.综合各种距离,通过多种策略去得到区域建议,最简单的方法当然是加权:
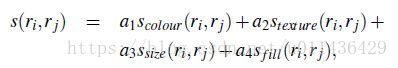
6.参数初始化多样性,我们基于基于图的图像分割得到初始区域,而这个初始区域对于最终的影响是很大的,因此我们通过多种参数初始化图像分割,也算是扩充了多样性。
给区域打分
通过上述的步骤我们能够得到很多很多的区域,但是显然不是每个区域作为目标的可能性都是相同的,因此我们需要衡量这个可能性,这样就可以根据我们的需要筛选区域建议个数啦。
这篇文章做法是,给予最先合并的图片块较大的权重,比如最后一块完整图像权重为1,倒数第二次合并的区域权重为2以此类推。但是当我们策略很多,多样性很多的时候呢,这个权重就会有太多的重合了,排序不好搞啊。文章做法是给他们乘以一个随机数,毕竟3分看运气嘛,然后对于相同的区域多次出现的也叠加下权重,毕竟多个方法都说你是目标,也是有理由的嘛。这样我就得到了所有区域的目标分数,也就可以根据自己的需要选择需要多少个区域了。
python实现:
# -*- coding: utf-8 -*-
from __future__ import division
import skimage.io
import skimage.feature
import skimage.color
import skimage.transform
import skimage.util
import skimage.segmentation
import numpy
# "Selective Search for Object Recognition" by J.R.R. Uijlings et al.
#
# - Modified version with LBP extractor for texture vectorization
def _generate_segments(im_orig, scale, sigma, min_size):
"""
segment smallest regions by the algorithm of Felzenswalb and
Huttenlocher
"""
# open the Image
im_mask = skimage.segmentation.felzenszwalb(
skimage.util.img_as_float(im_orig), scale=scale, sigma=sigma,
min_size=min_size)
# merge mask channel to the image as a 4th channel
im_orig = numpy.append(
im_orig, numpy.zeros(im_orig.shape[:2])[:, :, numpy.newaxis], axis=2)
im_orig[:, :, 3] = im_mask
return im_orig
def _sim_colour(r1, r2):
"""
calculate the sum of histogram intersection of colour
"""
return sum([min(a, b) for a, b in zip(r1["hist_c"], r2["hist_c"])])
def _sim_texture(r1, r2):
"""
calculate the sum of histogram intersection of texture
"""
return sum([min(a, b) for a, b in zip(r1["hist_t"], r2["hist_t"])])
def _sim_size(r1, r2, imsize):
"""
calculate the size similarity over the image
"""
return 1.0 - (r1["size"] + r2["size"]) / imsize
def _sim_fill(r1, r2, imsize):
"""
calculate the fill similarity over the image
"""
bbsize = (
(max(r1["max_x"], r2["max_x"]) - min(r1["min_x"], r2["min_x"]))
* (max(r1["max_y"], r2["max_y"]) - min(r1["min_y"], r2["min_y"]))
)
return 1.0 - (bbsize - r1["size"] - r2["size"]) / imsize
def _calc_sim(r1, r2, imsize):
return (_sim_colour(r1, r2) + _sim_texture(r1, r2)
+ _sim_size(r1, r2, imsize) + _sim_fill(r1, r2, imsize))
def _calc_colour_hist(img):
"""
calculate colour histogram for each region
the size of output histogram will be BINS * COLOUR_CHANNELS(3)
number of bins is 25 as same as [uijlings_ijcv2013_draft.pdf]
extract HSV
"""
BINS = 25
hist = numpy.array([])
for colour_channel in (0, 1, 2):
# extracting one colour channel
c = img[:, colour_channel]
# calculate histogram for each colour and join to the result
hist = numpy.concatenate(
[hist] + [numpy.histogram(c, BINS, (0.0, 255.0))[0]])
# L1 normalize
hist = hist / len(img)
return hist
def _calc_texture_gradient(img):
"""
calculate texture gradient for entire image
The original SelectiveSearch algorithm proposed Gaussian derivative
for 8 orientations, but we use LBP instead.
output will be [height(*)][width(*)]
"""
ret = numpy.zeros((img.shape[0], img.shape[1], img.shape[2]))
for colour_channel in (0, 1, 2):
ret[:, :, colour_channel] = skimage.feature.local_binary_pattern(
img[:, :, colour_channel], 8, 1.0)
return ret
def _calc_texture_hist(img):
"""
calculate texture histogram for each region
calculate the histogram of gradient for each colours
the size of output histogram will be
BINS * ORIENTATIONS * COLOUR_CHANNELS(3)
"""
BINS = 10
hist = numpy.array([])
for colour_channel in (0, 1, 2):
# mask by the colour channel
fd = img[:, colour_channel]
# calculate histogram for each orientation and concatenate them all
# and join to the result
hist = numpy.concatenate(
[hist] + [numpy.histogram(fd, BINS, (0.0, 1.0))[0]])
# L1 Normalize
hist = hist / len(img)
return hist
def _extract_regions(img):
R = {}
# get hsv image
hsv = skimage.color.rgb2hsv(img[:, :, :3])
# pass 1: count pixel positions
for y, i in enumerate(img):
for x, (r, g, b, l) in enumerate(i):
# initialize a new region
if l not in R:
R[l] = {
"min_x": 0xffff, "min_y": 0xffff,
"max_x": 0, "max_y": 0, "labels": [l]}
# bounding box
if R[l]["min_x"] > x:
R[l]["min_x"] = x
if R[l]["min_y"] > y:
R[l]["min_y"] = y
if R[l]["max_x"] < x:
R[l]["max_x"] = x
if R[l]["max_y"] < y:
R[l]["max_y"] = y
# pass 2: calculate texture gradient
tex_grad = _calc_texture_gradient(img)
# pass 3: calculate colour histogram of each region
for k, v in list(R.items()):
# colour histogram
masked_pixels = hsv[:, :, :][img[:, :, 3] == k]
R[k]["size"] = len(masked_pixels / 4)
R[k]["hist_c"] = _calc_colour_hist(masked_pixels)
# texture histogram
R[k]["hist_t"] = _calc_texture_hist(tex_grad[:, :][img[:, :, 3] == k])
return R
def _extract_neighbours(regions):
def intersect(a, b):
if (a["min_x"] < b["min_x"] < a["max_x"]
and a["min_y"] < b["min_y"] < a["max_y"]) or (
a["min_x"] < b["max_x"] < a["max_x"]
and a["min_y"] < b["max_y"] < a["max_y"]) or (
a["min_x"] < b["min_x"] < a["max_x"]
and a["min_y"] < b["max_y"] < a["max_y"]) or (
a["min_x"] < b["max_x"] < a["max_x"]
and a["min_y"] < b["min_y"] < a["max_y"]):
return True
return False
R = list(regions.items())
neighbours = []
for cur, a in enumerate(R[:-1]):
for b in R[cur + 1:]:
if intersect(a[1], b[1]):
neighbours.append((a, b))
return neighbours
def _merge_regions(r1, r2):
new_size = r1["size"] + r2["size"]
rt = {
"min_x": min(r1["min_x"], r2["min_x"]),
"min_y": min(r1["min_y"], r2["min_y"]),
"max_x": max(r1["max_x"], r2["max_x"]),
"max_y": max(r1["max_y"], r2["max_y"]),
"size": new_size,
"hist_c": (
r1["hist_c"] * r1["size"] + r2["hist_c"] * r2["size"]) / new_size,
"hist_t": (
r1["hist_t"] * r1["size"] + r2["hist_t"] * r2["size"]) / new_size,
"labels": r1["labels"] + r2["labels"]
}
return rt
def selective_search(
im_orig, scale=1.0, sigma=0.8, min_size=50):
'''Selective Search
Parameters
----------
im_orig : ndarray
Input image
scale : int
Free parameter. Higher means larger clusters in felzenszwalb segmentation.
sigma : float
Width of Gaussian kernel for felzenszwalb segmentation.
min_size : int
Minimum component size for felzenszwalb segmentation.
Returns
-------
img : ndarray
image with region label
region label is stored in the 4th value of each pixel [r,g,b,(region)]
regions : array of dict
[
{
'rect': (left, top, width, height),
'labels': [...],
'size': component_size
},
...
]
'''
assert im_orig.shape[2] == 3, "3ch image is expected"
# load image and get smallest regions
# region label is stored in the 4th value of each pixel [r,g,b,(region)]
img = _generate_segments(im_orig, scale, sigma, min_size)
if img is None:
return None, {}
imsize = img.shape[0] * img.shape[1]
R = _extract_regions(img)
# extract neighbouring information
neighbours = _extract_neighbours(R)
# calculate initial similarities
S = {}
for (ai, ar), (bi, br) in neighbours:
S[(ai, bi)] = _calc_sim(ar, br, imsize)
# hierarchal search
while S != {}:
# get highest similarity
i, j = sorted(S.items(), key=lambda i: i[1])[-1][0]
# merge corresponding regions
t = max(R.keys()) + 1.0
R[t] = _merge_regions(R[i], R[j])
# mark similarities for regions to be removed
key_to_delete = []
for k, v in list(S.items()):
if (i in k) or (j in k):
key_to_delete.append(k)
# remove old similarities of related regions
for k in key_to_delete:
del S[k]
# calculate similarity set with the new region
for k in [a for a in key_to_delete if a != (i, j)]:
n = k[1] if k[0] in (i, j) else k[0]
S[(t, n)] = _calc_sim(R[t], R[n], imsize)
regions = []
for k, r in list(R.items()):
regions.append({
'rect': (
r['min_x'], r['min_y'],
r['max_x'] - r['min_x'], r['max_y'] - r['min_y']),
'size': r['size'],
'labels': r['labels']
})
return img, regions
# -*- coding: utf-8 -*-
from __future__ import (
division,
print_function,
)
import skimage.data
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
import selectivesearch
def main():
# loading astronaut image
img = skimage.data.astronaut()
# perform selective search
img_lbl, regions = selectivesearch.selective_search(
img, scale=500, sigma=0.9, min_size=10)
candidates = set()
for r in regions:
# excluding same rectangle (with different segments)
if r['rect'] in candidates:
continue
# excluding regions smaller than 2000 pixels
if r['size'] < 2000:
continue
# distorted rects
x, y, w, h = r['rect']
if w / h > 1.2 or h / w > 1.2:
continue
candidates.add(r['rect'])
# draw rectangles on the original image
fig, ax = plt.subplots(ncols=1, nrows=1, figsize=(6, 6))
ax.imshow(img)
for x, y, w, h in candidates:
print(x, y, w, h)
rect = mpatches.Rectangle(
(x, y), w, h, fill=False, edgecolor='red', linewidth=1)
ax.add_patch(rect)
plt.show()
if __name__ == "__main__":
main()

