R语言之决策树CART、C4.5算法

决策树是以树的结构将决策或者分类过程展现出来，其目的是根据若干输入变量的值构造出一个相适应的模型，来预测输出变量的值。预测变量为离散型时，为分类树；连续型时，为回归树。
常用的决策树算法：

算法	简介	R包及函数
ID3	使用信息增益作为分类标准 ，处理离散数据，仅适用于分类树 。	rpart包 rpart()
CART	使用基尼系数作为分类标准，离散、连续数据均可，适用于分类树，回归树。	rpart包 rpart()
C4.5	使用信息增益和增益率相结合作为分类标准，离散、连续数据均可，但效率较低，适用于分类树	RWeka包 J48()
C5.0	是C4.5用于大数据集的拓展，效率较高	C50包 C5.0()

建模过程：
1）选定一个最佳变量将全部样本分为两类，并且实现两类中的纯度最大化，其分类标准有“信息增益”，“增益率”，“基尼系数”等。具体理论可参考周志华老师的《机器学习》一书。
2）对每一个分类子集重复步骤1）。
3）重复步骤1）、2），直到没有分类方法能将不纯度下降到给定的阈值以下。
4）根据步骤3）得出的模型预测所属类别。
用到的程序包rpart, raprt.plot. RWake, sampling, partykit。 建模所用数据为UCI机器学习数据库里的威斯康星州乳腺癌数据集和汽车数据集mtcars。仅以CART和C4.5算法函数的调用为例，C5.0算法的调用可用C50包中的C5.0()函数。

一、CART算法

步骤：
1、数据预处理，建立好训练集和预测集。代码如下：可参见《R语言实战》。

  > loc<-"http://archive.ics.uci.edu/ml/machine-learning-databases/"
> ds<-"breast-cancer-wisconsin/breast-cancer-wisconsin.data"
> url<-paste(loc,ds,sep="")
> data<-read.table(url,sep=",",header=F,na.strings="?")
> names(data)<-c("ID","clumpThickness","sizeUniformity",
+                  "shapeUniformity","maginalAdhesion",
+                  "singleEpithelialCellSize","bareNuclei",
+                  "blandChromatin","normalNucleoli",
+                  "mitosis","class")
> data$class[data$class==2]<-"良性"
> data$class[data$class==4]<-"恶性"
> data<-data[-1]
> set.seed(1234)
> train<-sample(nrow(data),0.7*nrow(data))
> tdata<-data[train,]
> vdata<-data[-train,]  

2、用rpart()构建树
rpart()函数的格式：
rpart(formula,data,weights,subsets,na.action=na.rpart,method,parms,control…)

参数	参数解释
formula	如y1~y2+y3+y4或者简写形式y1~.（表示输入变量为除y的所有变量）。
data	训练集。
subset	从data中选取子集建模。
na.action	缺失值处理，默认为na.rpart。表示剔除缺失y值或者缺失所有输入变量的数据。
method	选择决策树的类型。”anova”对应回归树。“class”用于分类变量，对应分类树。“poisson”用于二分类变量，对应分类树。“exp”用于生存分析。
parms	此参数只适用于分类变量。若method=”class”,则parms=list(split,prior,loss).其中split可取“information”(信息增益分类规则），“gini” (基尼分类规则）。不同的分类规则分别对应上述不同的算法。
control	控制树的各种参数。control=list(minsplit,minbucket=round(minsplit/3),…)
minsplit	每个节点中所含样本最小数，默认为10.当训练集样本数较少时，需自己设置此参数大小，否则可能因为样本数较少与此参数默认值冲突，导致画出来的树没有分支。
minbucket	叶节点中所含样本最小数.
cp	复杂度参数，通常设定阈值用来剪枝。

利用rpart()函数对上述的训练集建决策树。

> library(rpart)
> dtree<-rpart(class~.,data=tdata,method="class", parms=list(split="information"))  #使用ID3算法，若split="gini",则为CART算法。
> printcp(dtree)

Classification tree:
rpart(formula = class ~ ., data = tdata, method = "class", parms = list(split = "information"))

Variables actually used in tree construction:
[1] bareNuclei      clumpThickness  shapeUniformity sizeUniformity 

Root node error: 160/489 = 0.3272

n= 489 

        CP nsplit rel error  xerror     xstd
1 0.800000      0   1.00000 1.00000 0.064846
2 0.046875      1   0.20000 0.27500 0.039549
3 0.012500      3   0.10625 0.16875 0.031567
4 0.010000      4   0.09375 0.16875 0.031567

3、prune()剪枝，提高模型的泛化能力
格式： prune(tree,cp,…)

> dtree$cptable  #剪枝前的复杂度   nsplit分枝数  rel error训练集对应的误差   xerror 10折交叉验证误差  xstd交叉验证误差的标准差
        CP nsplit rel error  xerror       xstd
1 0.800000      0   1.00000 1.00000 0.06484605
2 0.046875      1   0.20000 0.27500 0.03954867
3 0.012500      3   0.10625 0.16875 0.03156665
4 0.010000      4   0.09375 0.16875 0.03156665
> tree<-prune(dtree,cp=0.0125)
> tree$cptable  #剪枝后的复杂度及分枝数
        CP nsplit rel error  xerror       xstd
1 0.800000      0   1.00000 1.00000 0.06484605
2 0.046875      1   0.20000 0.27500 0.03954867
3 0.012500      3   0.10625 0.16875 0.03156665

4、画出树图rpart.plot()
格式 rpart.plot(tree,type,fallen.leaves=T,branch,…)

参数	参数的解释
tree	画图所用的树模型。
type	可取1,2,3,4.控制图形中节点的形式。
fallen.leaves	默认值为T,在图的地段显示终端节点。
branch	控制图的外观。如branch=1，获得垂直树干的决策树。

树状图代码如下：

> opar<-par(no.readonly = T)
> par(mfrow=c(1,2))
> library(rpart.plot)
> rpart.plot(dtree,branch=1,type=2, fallen.leaves=T,cex=0.8, sub="剪枝前")
> rpart.plot(tree,branch=1, type=4,fallen.leaves=T,cex=0.8, sub="剪枝后")
> par(opar)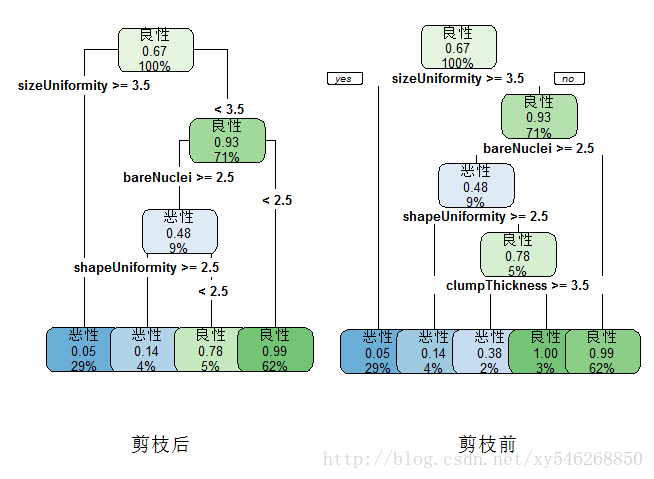

5、利用预测集检验模型效果predict()
格式 predict(fit,newdata,type,…)

> predtree<-predict(tree,newdata=vdata,type="class")   #利用预测集进行预测
> table(vdata$class,predtree,dnn=c("真实值","预测值"))    #输出混淆矩阵
      预测值
真实值 恶性 良性
  恶性   79    2
  良性    7  122

从混淆矩阵可以看出此模型准确率为（79+122）/（79+2+7+122）=95.71%

二、C4.5算法

RWeka包里的J48()可实现C4.5算法的调用。调用格式：
J48(formula,data,subset,na.action,control=Weka_control(u=T,c=0.25,M=2,R=T,N=3,B=T),options=NULL)

参数	参数的解释
U	默认值为TURE，表示不剪枝。
C	对剪枝过程设置的置信阈值。
M	默认值为2，表示叶节点最小样本量。
R	默认值为TURE，表示按错误率递减剪枝。
N	默认值为3，表示在R=T的情况下，交叉验证的折叠次数。
B	默认值为T，表示是否建立二叉树。

对R自带的数据集mtcars的变量mpg进行分类预测。
1、对mpg进行分组，创建训练集和预测集，代码如下：

> y<-quantile(mtcars$mpg,c(.8,.6,.4,.2))  #对mpg的数值取分位数
> mtcars$group[mtcars$mpg1]&mtcars$mpg>=y[2]]<-"A"  
> mtcars$group[mtcars$mpg2]&mtcars$mpg>=y[3]]<-"B"
> mtcars$group[mtcars$mpg3]&mtcars$mpg>=y[4]]<-"C"
> mtcars$group[mtcars$mpg4]]<-"D"
> mtcars$group<-factor(mtcars$group)   #将要预测的变量定义为因子，否则J48()函数无法识别
> a<-round(3/4*sum(mtcars$group=="A"))
> b<-round(3/4*sum(mtcars$group=="B"))
> c<-round(3/4*sum(mtcars$group=="C"))
> d<-round(3/4*sum(mtcars$group=="D"))
library(sampling) 
> sub<-strata(mtcars,stratanames="group",size=c(a,b,c,d),method="srswor")   #对分组变量采用分层抽样，保证样本的代表性
> tdata<-mtcars[sub$ID_unit,]   #训练集
> vdata<-mtcars[-sub$ID_unit,]   #预测集

2、创建分类树J48() `

> library(RWeka)                                                            
> ctree<-J48(group~.,data=tdata,control=Weka_control(M=2))
> print(ctree)
J48 pruned tree
------------------

mpg <= 19.7
|   mpg <= 14.7: D (5.0)
|   mpg > 14.7
|   |   mpg <= 17.8: C (4.0)
|   |   mpg > 17.8: B (4.0)
mpg > 19.7: A (10.0)

Number of Leaves  :     4

Size of the tree :     7
> library(partykit)
> plot(ctree,type="simple")  #画出树图，结果如下，由于训练集的数据较少，只有23条数据，最后的树图仅以mpg作为分支变量，也直接影响了最后的准确率。

3、预测predict()

> pretree<-predict(ctree,newdata=vdata)
> table(pretree,vdata$group,dnn=c("预测值","真实值"))  #输出混淆矩阵
      真实值
预测值 A B C D
     A 4 1 0 0
     B 0 0 0 0
     C 0 0 3 1
     D 0 0 0 0
> pretree
[1] A A C C C A A A C
Levels: A B C D
> vdata$group
[1] A A C C C A A B D
Levels: A B C D

准确率为77%。因为数据较少，所以准确率会稍低。