蒙特卡洛算法简单应用
蒙特卡洛算法概是以率统计理论为指导,使用随机数模拟来解决问题的一种方法
最简单的运用:
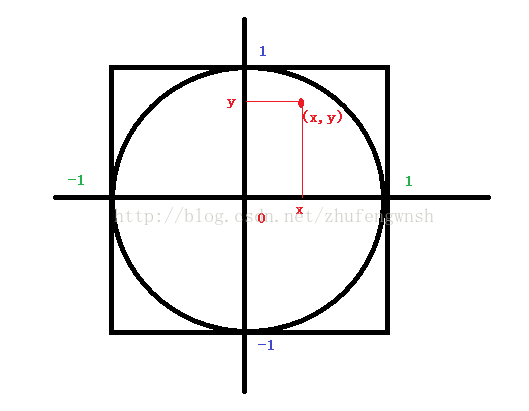
1.求圆周率π , 如果半径为1, 根据勾股定理,x² + y² <= 1 的落点都在圆内
正方形面积:2*2=4,圆面积:πr² = π
随机生成一个坐标,次数为a,假设有b次在圆内,那么 b/a(落在圆内部次数/落在正方形内部次数) = π/4(圆面积/正方形面积)
计算可得π=4*b/a
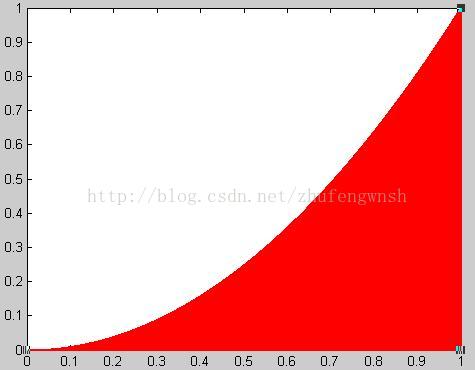
2:积分计算: 计算函数y=x² 在区间[0,1]的面积(红色部分的面积)
随机生成坐标,次数为a, 如果落点在红色区域,应该满足y<=x², 满足条件时累加,命中数为b
那么红色部分面积应该占的比例:b/a
package com.xp.test;
import java.util.Random;
/**
* 随机数计算圆周率π 蒙特卡洛算法的简单应用,还可用来计算积分等信息
*
* @author admin
*
*/
public class PI {
/**
* 判断落点是否在圆内部 勾股定理 x² + y² = r² ,那么 x² + y² <= r² 都视作在圆内
*
* @param x
* @param y
* @return
*/
public boolean isInCycle(double x, double y) {
if (x * x + y * y <= 1) {
return true;
} else {
return false;
}
}
public double getPi(int count) {
Random random = new Random();
double in = 0;
for (int i = 0; i < count; i++) {
double x = random.nextDouble();
double y = random.nextDouble();
if (isInCycle(x, y)) {
in++;
}
}
System.out.println(in + "/" + count);
return 4 * in / count;
}
/**
* 判断落点在积分线下的区域
*
* @param x
* @param y
* @return
*/
public boolean isInRegion(double x, double y) {
if (y <= x * x) {
return true;
} else {
return false;
}
}
public double getJifen(int count) {
Random random = new Random();
double in = 0;
for (int i = 0; i < count; i++) {
double x = random.nextDouble();
double y = random.nextDouble();
if (isInRegion(x, y)) {
in++;
}
}
System.out.println(in + "/" + count);
return in / count;
}
public static void main(String[] args) {
PI p = new PI();
// 求π,可以增加循环次数获取更精确结果
System.out.println(p.getPi(1000000));
// 求积分
System.out.println(p.getJifen(1000000));
}
}
785238.0/1000000
3.140952
332700.0/1000000
0.3327
参考:http://www.ruanyifeng.com/blog/2015/07/monte-carlo-method.html