利用硬件实现矩阵乘法加速

对于绝大多数程序员来说，优化程序往往是在算法方面。但了解一定的计算机硬件知识后，可以隐式地优化程序。下面以矩阵乘法为例，探讨计算机硬件在程序优化中的作用。

原理

学过计算机组成原理的都知道，CPU访问内存的速度比CPU计算速度慢得多，为了解决速度不匹配的问题，在CPU与内存之间加了高速缓存cache。cache的存在大大提高了CPU访问数据的速度。由于价格等原因，cache都比较小。因此，较好地利用cache可以加速程序运行。

方式一：ijk式

可以说是逻辑最为简单的方法来实现矩阵乘法。
i表示A的行标，j表示B的列标，k是A的列标同时也是B的行标，以实现对应位置的乘法，之后不再赘述。
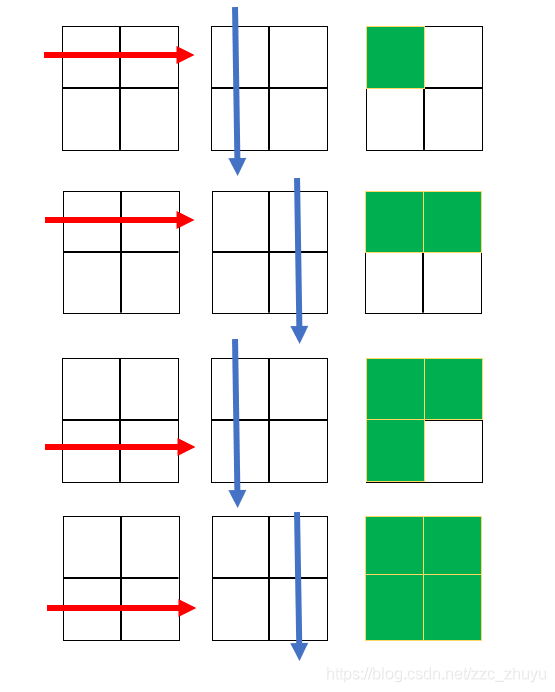
思想：一行一行地遍历A，一列一列地遍历B，A的一行与B的一列对应数值相乘（A[ i ][ k ]*B[ k ][ j ]）最后累加起来就得到了C的对应位置(C[ i ][ j ])上的值。与手动计算矩阵乘法的普通方式一致。（乘法逻辑见下图）。

方式二：jki式

思想：B是一列中单个元素单个元素地访问，A仍然是一行一行地遍历。A一行中的各个元素都与该元素相乘，得到的值放入C的一行里面。注意，此时C中各个位置上的值都是部分积，在遍历过程中需要累加这些部分积。当B的一行的元素都访问完毕后，才能得到最终结果。（乘法逻辑见下图）

方式三：kij式

思想：与方法二相似。A是一行中单个元素单个元素地访问，B是一列一列地遍历。A的这个元素与B一列中的各个元素相乘，得到的值放入C的一列里面。注意，此时C中各个位置上的值都是部分积，在遍历过程中需要累加这些部分积。当A的一列的元素都访问完毕后，才能得到最终结果。（乘法逻辑见下图）。

方式四：转置

思想：将矩阵B转置，得到B^T。这时要实现A*B^T=C。就是A的一行与B^T的一行相乘，可以采用方式一，只不过B^T的遍历方式为一列一列地遍历。（乘法逻辑见下图）。

方式五：分块

思想：将大矩阵（N*N）划分成若干小矩阵（B*B，B≪N）。对小矩阵做矩阵乘法得到的结果累加到C的对应位置中。注意，这时得到的也是部分积，当对应小矩阵全部计算累加完毕后，才能得到正确结果。对小矩阵的乘法可以采用以上方法，这里使用的是方式一。（乘法逻辑见下图）。

源代码（C语言）

#include 
#include 
#include 
#define N 512 //矩阵维度
#define b 64  //分块矩阵大小

int A[N][N];
int B[N][N];
int C[N][N];

void init(){ //初始化矩阵
	for(int i=0;i<N;i++){
		for(int j=0;j<N;j++){
			A[i][j]=rand();
			B[i][j]=rand();
		}
	}
}


void Transport(){ //矩阵B转置
	int temp;
	for(int i=0;i<N;i++){
		for(int j=0;j<N;j++){
			if(i>j){
				temp = B[i][j];
				B[i][j] = B[j][i];
				B[j][i] = temp;
			}
		}
	}
}

void IJK(){ //法1 ijk型
	int sum;
	int i, j, k;
	for(i=0; i<N; i++){
		for(j=0; j<N; j++){
			sum=0;
			for(k=0; k<N; k++){
				sum+=A[i][k] * B[k][j];
			C[i][j]=sum;
			}
		}
	}
}

void JKI(){ //法2 jki型
	int r;
	int i, j, k;
	for(j=0;j<N;j++){
		for(k=0;k<N;k++){
			r=B[k][j];
			for(i=0;i<N;i++){
				C[i][j]+=A[i][k]*r;
			}
		}
	}
}

void KIJ(){ //法3 kij型
	int r;
	int i, j, k;
	for(k=0;k<N;k++){
		for(i=0;i<N;i++){
			r=A[i][k];
			for(j=0;j<N;j++){
				C[i][j]+= r*B[k][j];
			}
		}
	}
}

void T(){ //法4 转置
	Transport();
	int sum;
	int i, j, k;
	for(i=0;i<N;i++){
		for(j=0;j<N;j++){
			sum=0;
			for(k=0;k<N;k++){
				sum+=A[i][k]*B[j][k];
			C[i][j]=sum;
			}
		}
	}
}


void Blocked() { //法5 分块矩阵
    int i, j, k;
    int i1, j1, k1;
    for (i = 0; i < N; i+=b)
    	for (j = 0; j < N; j+=b)
    		for (k = 0; k < N; k+=b)
    			for (i1 = i; i1 < i+b; i1++)
    				for (j1 = j; j1 < j+b; j1++)
    					for (k1 = k; k1 < k+b; k1++)
    						C[i1][j1] += A[i1][k1] * B[k1][j1];
}

实验结果

以512*512矩阵为例，探究以上五种方式的性能比较

int main(int argc,char*argv[])
{
	//ijk式
	init();
	clock_t start1, finish1;
	start1=clock();
	IJK();
	finish1=clock();
	double t1 = (double)(finish1-start1)/CLOCKS_PER_SEC;
	printf("ijk式:%f s\n",t1);

	//jki式
	init();
	clock_t start2, finish2;
	start2=clock();
	JKI();
	finish2=clock();
	double t2 = (double)(finish2-start2)/CLOCKS_PER_SEC;
	printf("jki式:%f s\n",t2);

	//kij式
	init();
	clock_t start3, finish3;
	start3=clock();
	KIJ();
	finish3=clock();
	double t3 = (double)(finish3-start3)/CLOCKS_PER_SEC;
	printf("kij式:%f s\n",t3);

	//转置
	init();
	clock_t start4, finish4;
	start4=clock();
	T();
	finish4=clock();
	double t4 = (double)(finish4-start4)/CLOCKS_PER_SEC;
	printf("转置:%f s\n",t4);

	//分块
	init();
	clock_t start5, finish5;
	start5=clock();
	Blocked();
	finish5=clock();
	double t5 = (double)(finish5-start5)/CLOCKS_PER_SEC;
	printf("分块:%f s\n",t5);
	
	return 0;
}

结果：

可以看到虽然得到相同的结果但是时间消耗差距很大。