DataLab 位运算
DataLab -位运算
- 知识储备
首先需要明白基本的一些操作符所代表的含义
按位与(&)、按位或(|)、按位异或(^)、按位加(+)、逻辑取反(!)、按位取反(~)、左移(<<)、右移(>>)
按位与运算将两个运算分量的对应位按位遵照以下规则进行计算:
0 & 0 = 0, 0 & 1 = 0, 1 & 0 = 0, 1& 1 = 1。
按位或运算将两个运算分量的对应位按位遵照以下规则进行计算:
0 | 0 = 0, 0 | 1 = 1, 1 | 0 = 1, 1 | 1 = 1
按位异或运算将两个运算分量的对应位按位遵照以下规则进行计算:
0 ^ 0 = 0, 0 ^1 = 1, 1 ^ 0 = 1, 1 ^ 1 = 0
按位加运算将两个运算分量的对应为按位遵照以下规则计算:
0+0=0,0+1=1,1+0=1,1+1=0
左移运算将一个位串信息向左移指定的位,右端空出的位用0补充,每左移1位相当于乘2
右移运算将一个位串信息向右移指定的位,右端移出的位的信息被丢弃,每右移1位,相当于除以2。对无符号数据,右移时,左端空出的位用0补充。对于带符号的数据,如果移位前符号位为0(正数),则左端也是用0补充;如果移位前符号位为1(负数),则左端用0或用1补充,取决于计算机系统。对于负数右移,称用0补充的系统为“逻辑右移”,用1补充的系统为“算术右移”。
按位取反为二进制串对应的1和0进行变换
逻辑取反只有0和非0两种情况
| 浮点数相关 | 符号位(1) | 阶码位(8) | 尾数(23) |
|---|---|---|---|
| 规格化 | 0 | !=0&!=255 | xxx xxxx xxxx xxxx xxxx xxxx |
| 非规格化 | x | 0000 0000 | xxx xxxx xxxx xxxx xxxx xxxx |
| 无穷大 | x | 1111 1111 | 000 0000 0000 0000 0000 0000 |
| NaN | x | 1111 1111 | !=0 |
- 题目分析:
/*
* bitAnd - x&y using only ~ and |
* Example: bitAnd(6, 5) = 4
* Legal ops: ~ |
* Max ops: 8
* Rating: 1
*/
int bitAnd(int x, int y) {
return ~(~x|~y);
}翻:使用~与|表示&符号。
根据布尔运算,a&b=~ (~ a|~b)可解决
/*
* getByte - Extract byte n from word x
* Bytes numbered from 0 (LSB) to 3 (MSB)
* Examples: getByte(0x12345678,1) = 0x56
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 6
* Rating: 2
*/
int getByte(int x, int n) {
return (x >> (n << 3)) & 0xFF;
}翻:取x字符串从右到左第n位字节(字节为0(低位)-3(高位))
x由16进制串构成,两个数字对应一个字节。由于小端存储,则右边为低位数字。所以首先需要右移8n位,然后使用&0xff取字节。但是此处没有 * 的方式,所以只能先对n进行位运算,使用n<<3代替8n,然后再进行右移,对x>>(n<<3)取最低位字节。
/*
* logicalShift - shift x to the right by n, using a logical shift
* Can assume that 0 <= n <= 31
* Examples: logicalShift(0x87654321,4) = 0x08765432
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 20
* Rating: 3
*/
int logicalShift(int x, int n) {
return (x>>n)&~(((1<<31)>>n)<<1);
}翻:字符串逻辑右移n位,且n属于0-31
本题需要考虑带符号数的正负性。由于正数补0负数补1,所以需要在移位之后对于前面补上的数进行操作使都为0。如果直接左移再右移,由于不清楚具体的位数可能导致吞掉除符号位外多的数。所以可以先让1前移31位(最大范围),然后再右移n-1位(此时第一位为1所以补位为1)。取反后便可以顺利保留原数位置的数为1而将扩展的符号数归0。之后两者相与即可将扩展位置0
/*
* bitCount - returns count of number of 1's in word
* Examples: bitCount(5) = 2, bitCount(7) = 3
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 40
* Rating: 4
*/
int bitCount(int x)
{
int mask1,mak2,mask4,mask8,mask16;
mask1 = 0x55 | 0x55 << 8;
mask1 = mask1 | mask1 << 16;
mask2 = 0x33 | 0x33 << 8;
mask2 = mask2 | mask2 << 16;
mask4 = 0x0F | 0x0F << 8;
mask4 = mask4 | mask4 << 16;
mask8 = 0xFF | 0xFF << 16;
mask16 = 0xFF | 0xFF << 8;
x = (x & mask1) + ((x >> 1) &mask1);
x = (x & mask2) + ((x >> 2) &mask2);
x = (x + (x >> 4)) & mask4;
x = (x + (x >> 8)) & mask8;
x = (x+ (x >> 16)) & mask16;
return x;
}翻:统计字符串中1的个数
这里可以使用类似于归并排序的方法。先将32位数分成两数一组,统计内部的1个数,得到16个二进制数。再分成两个数一组,此时相当于统计四个相邻数的1个数。然后循环统计,得到最后结果。共1,2,4,8,16五次统计。首先使用5(0101….)计算相邻元素,此时偏移一位就可以;然后使用3(0011….)计算,偏移两位;然后使用0f(00001111),偏移四位;然后使用00ff(0000 0000 1111 1111)偏移8位;然后使用0000ffff进行最后的统计,偏移16位。
由于dlc仅支持0x0-0xff范围内数字,所以需要额外操作得到我们需要的32位新数字。即对0x55进行两次移位,先移8位得01010101,再移16位得0101010101010101.其他类似。
但此时仍旧需要注意,起初的两次判断由于未组合完毕,会造成11111111这种组合完后为10101010的情况,此时若直接右移会造成符号扩展为1而非0造成错误。两次统计后,01000100便可避免该种情况。所以为了防止操作数超标,前两次采取分开相加偏移量,后三次可以相加后再进行偏移计算。
/*
* bang - Compute !x without using !
* Examples: bang(3) = 0, bang(0) = 1
* Legal ops: ~ & ^ | + << >>
* Max ops: 12
* Rating: 4
*/
int bang(int x) {
return (((~x+1)|x)>>31)+1;
}翻:使用其他符号表示!的作用,即0输出1,非0输出0。
发现0的相反数为0,其余数相反数符号相反。于是二者相或后首位为1的为非0数,为0的为0。根据题目,为0时输出1,所以计算最后结果再+1
/*
* tmin - return minimum two's complement integer
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 4
* Rating: 1
*/
int tmin(void) {
return 1<<31;
}翻:找出最小的补码
发现恰好就是1<<31位的数字,直接输出
/*
* fitsBits - return 1 if x can be represented as an
* n-bit, two's complement integer.
* 1 <= n <= 32
* Examples: fitsBits(5,3) = 0, fitsBits(-4,3) = 1
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 15
* Rating: 2
*/
int fitsBits(int x, int n) {
int expend=32+~n+1;
return !(x^(x<<expend>>expend));
}翻:x的二进制能否被n位进制表示
此处以样例分析,x=-4对应的存储为补码,32位为
1111 1111 1111 1111 1111 1111 1111 1100。
已知可以用3位表示但不可用2位表示,则发现若对其进行左移再右移操作时,3位扩展32-3=29位时
1111 1111 1111 1111 1111 1111 1111 1100,
2位扩展32-2=30位时
0000 0000 0000 0000 0000 0000 0000 0000。
同样,x=5时存储为
0000 0000 0000 0000 0000 0000 0000 0101,
已知可以用4位表示但不可以用3位。
如果扩展32-3=29位时产生
1111 1111 1111 1111 1111 1111 1111 1101错误,
扩展32-4=28位时
0000 0000 0000 0000 0000 0000 0000 0101.
则发现对应扩展32-n符号位后是否与原值一致可以判断是否可以用n位数表示,该判断和使用^实现。最后结果根据题意进行逻辑取反。
/*
* divpwr2 - Compute x/(2^n), for 0 <= n <= 30
* Round toward zero
* Examples: divpwr2(15,1) = 7, divpwr2(-33,4) = -2
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 15
* Rating: 2
*/
int divpwr2(int x, int n){
int sign=x>>31;
int mask=(1<<n)+(~0);
int bias=sign&mask;
return (x+bias)>>n;;
}翻:计算x/(2^n) 翻:计算-x 翻:判断是正数还是负数 首先判定符号位确定正负,正为0负为1,由于输出恰好相反,则!(x>>31)。然后考虑0的情况。根据逻辑!判断是否为0,所以或上!x可判断,此时修改为!((x>>31)|!x)恰好满足要求。先移动符号位,再根据是否为0综合判断 翻:判断x,y的大小 首先判断符号。如果是异号,则根据x判断,x负返1,x正返0,此时异或为1,保证结果所以直接&x的符号位;如果是同号,则对x取补码,计算y-x,再根据其符号位进行运算。此时异或为0,为了保证与y-x符号位相关,在异或中添1使为1,再与上subsign的最终值。由于正负相反与输出,加上!取反 翻:计算x为2的多少次幂 翻:返回相反数,超过NaN返回原值 翻:强制转型Int到float 先判断是否为0,为0直接返回。然后判断符号位,负数则符号位设负,数值转正。正数不用转换。接下来循环寻找小数位与阶码位。absx循环左移查找第一位有效数字非0的位置,并且shiftleft记录移动的次数。找到后停止循环。由于这个数不会计入最后的尾码部分,所以再次左移一位(如0.0110=>1.10)。则可以发现,将此时的字串右移9位即可得到最终的尾码部分。127+(32-shiftleft)判断阶码位的数值,左移23位到达对应的位置。 但此时会出现问题,即int使用了31位表示精度,float仅23位,所以虽然float的范围较大,但是此时可能会产生精度丢失的问题。现在提取出会被舍去的部分,也就是absx的从左往右后9位,可以用和0x01ff的与操作,提取出来,如果这一部分是大于256(0x0100)的,那么应该有进位操作;如果这一部分是等于256且absx左往右倒数第10位上是 数字1的话,也应该有进位,这种情况的判断是和0x03ff与操作,看结果是否与0x0300相等。 根据if判断在这两种情况下都使得flag=1,最后可以将求得的符号部分,exp部分,frac部分, 和最后的进位部分相加就能得到最后的结果。 例: 翻:求float数据的两倍,若为NaN,返回NaN https://blog.csdn.net/the_v_/article/details/45423503 http://www.cnblogs.com/graphics/archive/2010/06/21/1752421.html https://blog.csdn.net/werewolf_ace/article/details/49924743 https://blog.csdn.net/weixin_41256413/article/details/80172553 https://blog.csdn.net/LittleLove1201/article/details/50730936
正数除法可以直接移位进行,但是对于负数向下取整,-33/16在计算机中会变成-3.如果要变成-2,则需要添加一个偏置量将数的范围从(-3,-2)变成(-2,1)。关于偏置量的取值,当a>=0时,偏置量值为0;当a<0时,设偏移量为n,偏置量取值为(2^n-1)。则先取符号位sign=x>>31,再取偏置值为mask=(1</*
* negate - return -x
* Example: negate(1) = -1.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 5
* Rating: 2
*/
int negate(int x) {
return ~x+1;
}
补码定义,按位取反+1。/*
* isPositive - return 1 if x > 0, return 0 otherwise
* Example: isPositive(-1) = 0.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 8
* Rating: 3
*/
int isPositive(int x) {
return !((x>>31)|!x);
}/*
* isLessOrEqual - if x <= y then return 1, else return 0
* Example: isLessOrEqual(4,5) = 1.
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 24
* Rating: 3
*/
int isLessOrEqual(int x, int y) {
int signx=(x>>31)&0x1;
int signy=(y>>31)&0x1;
int subsign=((y+(~x+1))>>31)&0x1;
return ((signx^signy)&signx)+((signx^signy^1)&!subsign);
}/*
* ilog2 - return floor(log base 2 of x), where x > 0
* Example: ilog2(16) = 4
* Legal ops: ! ~ & ^ | + << >>
* Max ops: 90
* Rating: 4
*/
int ilog2(int x) {
int result;
result=(!!(x >> 16)) << 4;
result += ((!!(x >> (result+8))) << 3);
result += ((!!(x >> (result+4))) << 2);
result += ((!!(x >> (result+2))) << 1);
result += (!!(x >> (result+1)));
return result;
}
本质是求最高位的1的位置。所以可以将二进制串右移实现。!!(x<
0100+0。所以最高位为4。/*
* float_neg - Return bit-level equivalent of expression -f for
* floating point argument f.
* Both the argument and result are passed as unsigned int's, but
* they are to be interpreted as the bit-level representations of
* single-precision floating point values.
* When argument is NaN, return argument.
* Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
* Max ops: 10
* Rating: 2
*/
unsigned float_neg(unsigned uf) {
unsigned result= uf ^ 0x80000000;
unsigned tmp=uf & 0x7fffffff;
if( tmp > 0x7f800000 ) result=uf;
return result;
}
此函数要求求相反数,浮点数的相反数只需要改变符号位就可以。且题目要求内出现了NaN。所以需要对是否超越NaN进行判断。先用0x8000000其符号位改变后的情况放在result中,再使用tmp保留除符号位外的值,0x7f800000为无穷大,界限NaN,所以将其与tmp比较,NaN以上返回原值,否则返回相反数。/*
* float_i2f - Return bit-level equivalent of expression (float) x
* Result is returned as unsigned int, but
* it is to be interpreted as the bit-level representation of a
* single-precision floating point values.
* Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
* Max ops: 30
* Rating: 4
*/
unsigned float_i2f(int x) {
unsigned sign=0,shiftleft=1,flag=0;
unsigned absx=x;
if( x==0 ) return 0;
if( x<0 ){
sign=0x80000000;
absx=(~x+1);
}
while((absx&0x80000000)==0){
absx<<=1;
shiftleft++;
}
absx<<=1;
if( (absx & 0x01ff) > 0x0100 ) flag=1;
if( (absx & 0x03ff) == 0x0300 ) flag=1;
return sign+((127+(32-shiftleft))<<23)+(absx>>9)+flag;
}
1111 1111 1111 1111 1000 1000 1000 1000
0000 0000 0000 0000 0111 0111 0111 1000
1 11 0111 0111 1000 ==1.1101 1101 1110 0000 0000 0000 0000 0000
shiftleft=18
符号码:1
阶码:
127+32-18=141=128+8+4+1=>1000 1101
尾码:
1101 1101 1110 0000 0000 000
Flag:0
结果:
1100 0110 1110 1110 1111 0000 0000 0000/*
1. float_twice - Return bit-level equivalent of expression 2*f for
2. floating point argument f.
3. Both the argument and result are passed as unsigned int's, but
4. they are to be interpreted as the bit-level representation of
5. single-precision floating point values.
6. When argument is NaN, return argument
7. Legal ops: Any integer/unsigned operations incl. ||, &&. also if, while
8. Max ops: 30
9. Rating: 4
*/
unsigned float_twice(unsigned uf) {
if ((uf & 0x7F800000) == 0){
uf = ((uf & 0x007FFFFF)<<1) | (0x80000000 & uf);
}else if ((uf & 0x7F800000) != 0x7F800000){
uf =uf+0x00800000;
}
return uf;
}
浮点数运算时需要考虑符号阶码尾数。
如果阶码为0,那么就是非规格数,直接将尾数左移1位到阶码域上,其他不变。同时需要对符号位进行判定。
如果阶码不为0且不是255,那么直接阶码加1即可。
如果阶码为255,那么是NaN,∞,-∞,直接返回。

3. 最终结果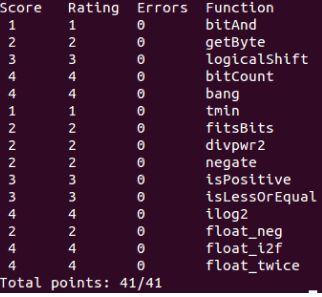
参考资料:
https://blog.csdn.net/qq_19762007/article/details/80038755