隐马尔可夫模型(上)基本概念
隐马尔可夫模型(hidden Markov model,HMM)是可用于标注问题的统计学习模型,描述由隐藏的马尔可夫链随机生成观测序列的过程,属于生成模型。
基本概念
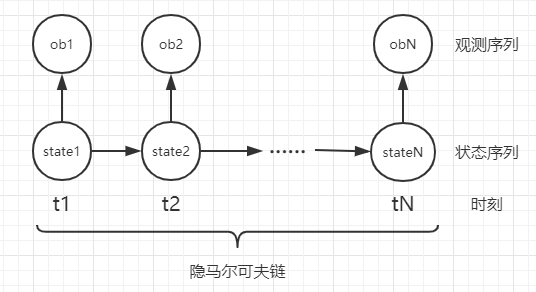
隐马尔可夫模型是关于时序的概率模型,描述由一个隐藏的马尔可夫链随机生成不可观测的状态随机序列,再由各个状态生成一个观测从而产生观测随机序列的过程。
- 状态序列(state sequence):隐藏的马尔可夫链随机生成的状态序列;
- 观测序列(observation sequence):每个状态生成一个观测,而由此产生的观测的随机序列。
- 时刻:序列的每一个位置。
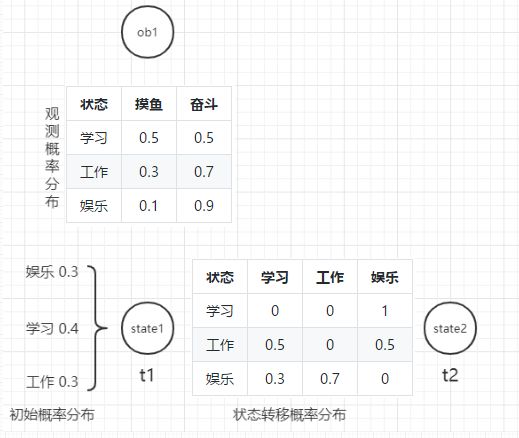
通过上图我们可以清楚地看到,状态序列是基于马尔可夫链的性质生成的——当前时刻的状态仅依赖于前一时刻的状态。状态序列中每个状态生成一个专属于当前状态的观测,因此生成了一条观测序列。此外,这条马尔可夫链是无法被观测到的,因此被称为隐马尔可夫模型。
我们可以将上图的隐马尔可夫模型结构图拆分为静态和动态两部分来理解:
- 静态:模型各个节点所代表的含义;
- 动态:数据在模型各个节点的流动。
上图中的所有 state 即为状态的集合,我们用 Q 来表示,用 S 来表示状态的数目;所有的 ob 即为观测的集合,用 V 来表示,用 M 来表示观测的数目。N 表示序列的长度(这里和《统计学习方法》略有不同,使用 S 来表示状态的数目,N 表示序列的长度,这主要是绘制图的时候用 N 代替了 T,捂脸哭.jpg)。
Q = { q 1 , q 2 , … , q S } , V = { v 1 , v 2 , … , v M } I = ( i 1 , i 2 , … , i N ) , O = ( o 1 , o 2 , … , o N ) Q = \{q_1, q_2, \ldots, q_S\}, \quad V = \{v_1, v_2, \ldots, v_M\} \\ I = (i_1, i_2, \ldots, i_N), \quad O = (o_1, o_2, \ldots, o_N) Q={ q1,q2,…,qS},V={ v1,v2,…,vM}I=(i1,i2,…,iN),O=(o1,o2,…,oN)
接下来,我们就来了解下隐马尔可夫模型是如何根据马尔可夫链从第一个状态开始,不断随着时间的增长,从而生成一条状态序列。
举个不恰当的例子,我们将人一天的行为归纳为三种状态:娱乐、学习和工作。在这个例子中,状态集合 Q = {娱乐, 学习, 工作},S = 3,即 q1 = 娱乐、q2 = 学习、q3 = 工作。
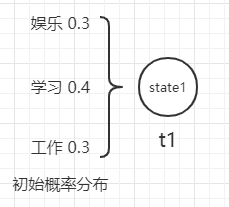
首先,我们需要确定处于起始时刻人的状态,此时有三种可能:娱乐、学习和工作,每个状态都有相应的发生概率,假设娱乐的概率为 0.3,学习的概率为 0.4,工作的概率为 0.3。这相当于我们为初始时刻的状态设定了一个状态的概率分布,在隐马尔可夫模型中被称为初始概率分布。
通常我们会用 π 来表示初始状态概率向量:
π = ( π i ) π i = P ( i 1 = q i ) , i = 1 , 2 , … , S \pi = (\pi_i) \quad \pi_i = P(i_1 = q_i), i =1, 2, \ldots, S π=(πi)πi=P(i1=qi),i=1,2,…,S
表示时刻 t = 1 处于状态 qi 的概率。在该例子中:
π 1 = P ( i 1 = q 1 = 娱乐 ) = 0.3 π 1 = P ( i 1 = q 2 = 学习 ) = 0.4 π 1 = P ( i 1 = q 3 = 工作 ) = 0.3 \pi_1 = P(i_1=q_1=\text{娱乐}) = 0.3 \\ \pi_1 = P(i_1=q_2=\text{学习}) = 0.4 \\ \pi_1 = P(i_1=q_3=\text{工作}) = 0.3 π1=P(i1=q1=娱乐)=0.3π1=P(i1=q2=学习)=0.4π1=P(i1=q3=工作)=0.3
接着,我们需要根据初始时刻(t1)的状态来生成下一个时刻(t2)的状态。假设,初始时刻 t1 的状态为学习,但因为人是有惰性的,前一天学习后,第二天就不会选择学习和工作。因此,t2 时刻的状态只能为娱乐。如果将娱乐、学习和工作当作数据结构中图的三个顶点,则状态间的跳转相当于顶点之间的有向边,例如学习->娱乐,表示从顶点“学习”指向顶点“娱乐”。
我们可以根据状态间的跳转来建立一个状态跳转概率矩阵:
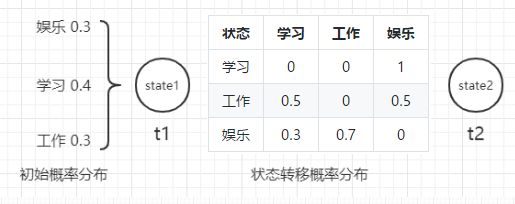
| 状态 | 学习 | 工作 | 娱乐 |
|---|---|---|---|
| 学习 | 0 | 0 | 1 |
| 工作 | 0.5 | 0 | 0.5 |
| 娱乐 | 0.3 | 0.7 | 0 |
状态跳转概率矩阵表示从当前状态跳转到下一个状态的概率。看第三行,从“娱乐”跳转到“学习”和“工作”的概率分别为 30% 和 70%,这表示前一时刻的状态为“娱乐”,则现在的状态更有可能是“工作”。
通过状态跳转概率矩阵,我们就可以通过前一时刻的状态来计算当前时刻最有可能的状态。在隐马尔可夫模型中,状态跳转概率矩阵被称为状态转移概率分布,通常用 A 来表示。
A = [ a i j ] S × S , a i j = P ( i t + 1 = q j ∣ i t = q i ) , i = 1 , 2 , … , S ; j = 1 , 2 , … , S A = [a_{ij}]_{S \times S}, \quad a_{ij} = P(i_{t+1}=q_j|i_t=q_i), i = 1, 2, \ldots, S; j = 1, 2, \ldots, S A=[aij]S×S,aij=P(it+1=qj∣it=qi),i=1,2,…,S;j=1,2,…,S
表示从时刻 t 状态 qi 转移到时刻 t + 1 状态 qj 的概率。在该例子中:
a 11 = P ( i t + 1 = 学 习 ∣ i t = 学 习 ) = 0.0 a 12 = P ( i t + 1 = 学 习 ∣ i t = 工 作 ) = 0.0 a 13 = P ( i t + 1 = 学 习 ∣ i t = 娱 乐 ) = 1.0 a 21 = P ( i t + 1 = 工 作 ∣ i t = 学 习 ) = 0.5 a 22 = P ( i t + 1 = 工 作 ∣ i t = 工 作 ) = 0.0 a 23 = P ( i t + 1 = 工 作 ∣ i t = 娱 乐 ) = 0.5 a 31 = P ( i t + 1 = 娱 乐 ∣ i t = 学 习 ) = 0.3 a 32 = P ( i t + 1 = 娱 乐 ∣ i t = 工 作 ) = 0.7 a 33 = P ( i t + 1 = 娱 乐 ∣ i t = 学 习 ) = 0.0 A = [ 0.0 0.0 1.0 0.5 0.0 0.5 0.3 0.7 0.0 ] a_{11} = P(i_{t+1}=学习|i_t=学习) = 0.0 \\ a_{12} = P(i_{t+1}=学习|i_t=工作) = 0.0 \\ a_{13} = P(i_{t+1}=学习|i_t=娱乐) = 1.0 \\ a_{21} = P(i_{t+1}=工作|i_t=学习) = 0.5 \\ a_{22} = P(i_{t+1}=工作|i_t=工作) = 0.0 \\ a_{23} = P(i_{t+1}=工作|i_t=娱乐) = 0.5 \\ a_{31} = P(i_{t+1}=娱乐|i_t=学习) = 0.3 \\ a_{32} = P(i_{t+1}=娱乐|i_t=工作) = 0.7 \\ a_{33} = P(i_{t+1}=娱乐|i_t=学习) = 0.0 \\ A = \begin{bmatrix} 0.0 & 0.0 & 1.0 \\ 0.5 & 0.0 & 0.5 \\ 0.3 & 0.7 & 0.0 \\ \end{bmatrix} a11=P(it+1=学习∣it=学习)=0.0a12=P(it+1=学习∣it=工作)=0.0a13=P(it+1=学习∣it=娱乐)=1.0a21=P(it+1=工作∣it=学习)=0.5a22=P(it+1=工作∣it=工作)=0.0a23=P(it+1=工作∣it=娱乐)=0.5a31=P(it+1=娱乐∣it=学习)=0.3a32=P(it+1=娱乐∣it=工作)=0.7a33=P(it+1=娱乐∣it=学习)=0.0A=⎣⎡0.00.50.30.00.00.71.00.50.0⎦⎤
最后,我们需要根据生成的状态序列去生成观测序列。假设,现在有两种观测结果:摸鱼和奋斗。此时观测集合 V = {摸鱼, 奋斗},M = 2,V1 = 摸鱼、V2 = 奋斗。
| 状态 | 摸鱼 | 奋斗 |
|---|---|---|
| 学习 | 0.5 | 0.5 |
| 工作 | 0.3 | 0.7 |
| 娱乐 | 0.1 | 0.9 |
在隐马尔可夫模型中,上表被称为观测概率分布,通常用 B 来表示:
B = [ b j ( k ) ] S × M b j ( k ) = P ( o t = v k ∣ i t = q j ) , k = 1 , 2 , … , M ; j = 1 , 2 , … , S B = [b_j(k)]_{S \times M} \quad b_j(k) = P(o_t=v_k|i_t=q_j), k = 1, 2, \ldots, M; j = 1, 2, \ldots, S B=[bj(k)]S×Mbj(k)=P(ot=vk∣it=qj),k=1,2,…,M;j=1,2,…,S
表示从时刻 t 状态 qj 的条件下生成观测 vk 的概率,在该例子中:
b 1 ( 1 ) = P ( o t = v 1 = 摸鱼 ∣ i t = q 1 = 学习 ) = 0.5 b 1 ( 2 ) = P ( o t = v 2 = 奋斗 ∣ i t = q 1 = 学习 ) = 0.5 b 2 ( 1 ) = P ( o t = v 1 = 摸鱼 ∣ i t = q 2 = 工作 ) = 0.3 b 2 ( 2 ) = P ( o t = v 2 = 奋斗 ∣ i t = q 2 = 工作 ) = 0.7 b 3 ( 1 ) = P ( o t = v 1 = 摸鱼 ∣ i t = q 3 = 娱乐 ) = 0.1 b 3 ( 2 ) = P ( o t = v 2 = 奋斗 ∣ i t = q 3 = 娱乐 ) = 0.9 B = [ 0.5 0.5 0.3 0.7 0.1 0.9 ] b_1(1) = P(o_t = v_1 = \text{摸鱼}|i_t = q_1 = \text{学习}) = 0.5 \\ b_1(2) = P(o_t = v_2 = \text{奋斗}|i_t = q_1 = \text{学习}) = 0.5 \\ b_2(1) = P(o_t = v_1 = \text{摸鱼}|i_t = q_2 = \text{工作}) = 0.3 \\ b_2(2) = P(o_t = v_2 = \text{奋斗}|i_t = q_2 = \text{工作}) = 0.7 \\ b_3(1) = P(o_t = v_1 = \text{摸鱼}|i_t = q_3 = \text{娱乐}) = 0.1 \\ b_3(2) = P(o_t = v_2 = \text{奋斗}|i_t = q_3 = \text{娱乐}) = 0.9 \\ B = \begin{bmatrix} 0.5 & 0.5 \\ 0.3 & 0.7 \\ 0.1 & 0.9 \\ \end{bmatrix} b1(1)=P(ot=v1=摸鱼∣it=q1=学习)=0.5b1(2)=P(ot=v2=奋斗∣it=q1=学习)=0.5b2(1)=P(ot=v1=摸鱼∣it=q2=工作)=0.3b2(2)=P(ot=v2=奋斗∣it=q2=工作)=0.7b3(1)=P(ot=v1=摸鱼∣it=q3=娱乐)=0.1b3(2)=P(ot=v2=奋斗∣it=q3=娱乐)=0.9B=⎣⎡0.50.30.10.50.70.9⎦⎤
通过初始概率分布、状态转移概率分布和观测概率分布,我们就可以生成状态序列和观测序列!
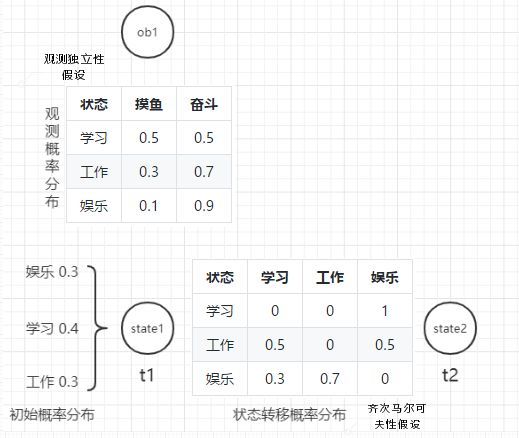
需要注意的是,隐马尔可夫模型满足两个基本假设:
- 齐次马尔可夫性假设:假设隐藏的马尔可夫链在任意时刻 t 的状态只依赖于其前一时刻的状态,与其他时刻的状态及观测无关,也与时刻 t 无关。
P ( i t ∣ i t − 1 , o t − 1 , ⋯ , i 1 , o 1 ) = P ( i t ∣ i t − 1 ) , t = 1 , 2 , ⋯ , N P(i_t|i_{t-1}, o_{t-1}, \cdots, i_1, o_1) = P(i_t|i_{t-1}), \qquad t = 1, 2, \cdots, N P(it∣it−1,ot−1,⋯,i1,o1)=P(it∣it−1),t=1,2,⋯,N - 观测独立性假设:假设任意时刻的观测只依赖于该时刻的马尔可夫链的状态,与其他观测及状态无关。
P ( o t ∣ i N , o N , i N − 1 , o N − 1 ⋯ , i t + 1 , o t + 1 , i t , i t − 1 , o t − 1 , ⋯ , i 1 , o 1 ) = P ( o t ∣ i t ) P(o_t|i_N, o_N, i_{N-1}, o_{N-1} \cdots, i_{t+1}, o_{t+1}, i_t, i_{t-1}, o_{t-1}, \cdots, i_1, o_1) = P(o_t|i_t) P(ot∣iN,oN,iN−1,oN−1⋯,it+1,ot+1,it,it−1,ot−1,⋯,i1,o1)=P(ot∣it)
上面是完整的模型结构图,从初始概率分布出发选择 t1 时刻的状态。然后:
- 根据观测概率分布以及当前时刻 t1 的状态来确定观测结果;
- 根据状态转移概率分布以及当前时刻 t1 的状态来确定下一时刻 t2 的状态。
由上所得,隐马尔可夫模型由初始状态概率向量 π、状态转移概率矩阵 A 和观测概率矩阵 B 决定。
- π 和 A 确定隐藏的马尔可夫链,生成不可预测的状态序列。
- B 确定如何从状态生成观测,与状态序列综合确定了如何产生观测序列。
【符号表示】:
λ = ( A , B , π ) \lambda = (A, B, \pi) λ=(A,B,π)
A、B、π 称为隐马尔可夫模型的三要素。
【PS】:因篇幅过长故而将其拆分为两部分,在本篇博客中介绍隐马尔可夫模型的基本概念,在下一篇博客中会具体介绍隐马尔可夫模型的计算和应用。