模型优化-RMSprop
RMSprop 全称 root mean square prop 算法,和动量方法一样都可以加快梯度下降速度。关于动量方法的内容可以参考这篇博文模型优化-动量方法。
动量方法借助前一时刻的动量,从而能够有效地缓解山谷震荡以及鞍部停滞问题。而 RMSprop 对比动量方法的思想有所不同,以 y = wx + b 为例,因为只有两个参数,因此可以通过可视化的方式进行说明。
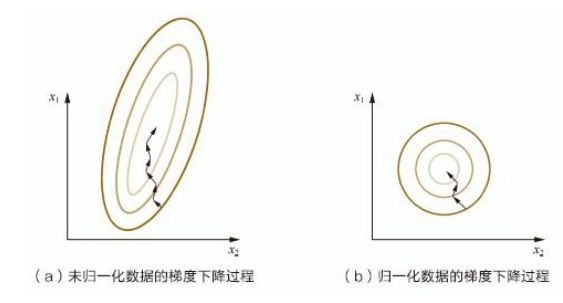
假设纵轴代表参数 b,横轴代表参数 w,由于 w 的取值大于 b,因此整个梯度的等高线呈椭圆形。可以看到越接近最低点(谷底),椭圆的横轴与纵轴的差值也越大,正好对应我们先前所说的山谷地形。
上图中可以看到每个点的位置,以及这些点的梯度方向,也就是说,每个位置的梯度方向垂直于等高线。那么在山谷附近,虽然横轴正在推进,但纵轴方向的摆动幅度也越来越大,这就是山谷震荡现象。如果使用的随机梯度下降,则很有可能不断地上下震荡而无法收敛到最优值附近。所以,我们向减缓参数 b 方向(纵轴)的速度,同时加快参数 w 方向(横轴)的速度。
【计算过程】:
-
单独计算每个参数在当前位置的梯度。
d w i = ∂ L ( w ) ∂ w i dw_{i} = \frac{\partial L(w)}{\partial w_i} dwi=∂wi∂L(w) -
计算更新量。
S d w i = β S d w i + ( 1 − β ) d w i 2 Sdw_{i} = \beta Sdw{i} + (1 - \beta)dw_{i}^2 Sdwi=βSdwi+(1−β)dwi2
需要注意的是 d w 2 dw^2 dw2 是指对 dw 做平方处理。 -
更新参数。
w i = w i − η d w i S d w i w_i = w_i - \eta \frac{dw_i}{\sqrt{Sdw_i}} wi=wi−ηSdwidwi
需要注意 S d w i Sdw_i Sdwi 有可能为 0,因此可以添加一个极小的常数来防止分母为零的情况出现。
w i = w i − η d w i σ + S d w i w_i = w_i - \eta \frac{dw_i}{\sigma + \sqrt{Sdw_i}} wi=wi−ησ+Sdwidwi
也可以把这个极小的值放到根号里面。
w i = w i − η d w i σ + S d w i w_i = w_i - \eta \frac{dw_i}{\sqrt{\sigma + Sdw_i}} wi=wi−ησ+Sdwidwi
根据参数更新公式, S d w i Sdw_i Sdwi 越大,则 w 更新得越慢。在先前所讲的山谷地形中,纵轴方向的梯度要大于横轴方向的梯度,也就是说 db 远大于 dw, d b / S d b db/\sqrt{Sdb} db/Sdb 值要小于 d w / S d w dw/\sqrt{Sdw} dw/Sdw,最终在纵轴方向上更新得较慢,而在横轴上更新得更快。
RMSprop 实际上是将椭圆形的等高线转换为圆形的等高线。怎么理解呢?当采用特征归一化将 w 和 b 都转化为 [0, 1] 区间后,此时的图等同于右图。
因为是圆形,无论是纵轴还是横轴的梯度大小都相等,那么计算得到的更新量 Sdw = Sdb。若等高线呈椭圆形,则椭圆形长轴方向更新量要大于椭圆形短轴方向,就好比长轴长度为 10,短轴长度为 5,长轴方向每次更新 1,短轴方向每次更新 0.5。虽然速度上不想等,但两者最终从一端抵达另一端所需的时间是一致的。这也是为什么我将 RMSprop 理解成将椭圆形等高线转换为圆形。
【代码实现】:
def RMSprop(x, y, step=0.01, iter_count=500, batch_size=4, beta=0.9):
length, features = x.shape
data = np.column_stack((x, np.ones((length, 1))))
w = np.zeros((features + 1, 1))
Sdw, eta = 0, 10e-7
start, end = 0, batch_size
for i in range(iter_count):
# 计算梯度
dw = np.sum((np.dot(data[start:end], w) - y[start:end]) * data[start:end], axis=0) / length
# 计算更新量
Sdw = beta * Sdw + (1 - beta) * np.dot(dw, dw)
# 更新参数
w = w - (step / np.sqrt(eta + Sdw)) * dw.reshape((features + 1, 1))
start = (start + batch_size) % length
if start > length:
start -= length
end = (end + batch_size) % length
if end > length:
end -= length
return w
对比 AdaGrad 的实现代码,我们可以发现 RMSprop 实际上在 AdaGrad 的梯度累积平方计算公式上新增了一个衰减系数 β 来控制历史信息的获取。
- AdaGrad:
r = r + d w 2 r = r + dw^2 r=r+dw2 - RMSprop:
S d w = β S d w + ( 1 − β ) d w 2 Sdw = \beta Sdw + (1 - \beta)dw^2 Sdw=βSdw+(1−β)dw2
从这个角度来说,RMSprop 改变了学习率。
RMSprop 算法可以结合牛顿动量,RMSprop 改变了学习率,而牛顿动量改变了梯度,从两方面改变更新方式。
【代码实现】:
def RMSprop(x, y, step=0.01, iter_count=500, batch_size=4, alpha=0.9, beta=0.9):
length, features = x.shape
data = np.column_stack((x, np.ones((length, 1))))
w = np.zeros((features + 1, 1))
Sdw, v, eta = 0, 0, 10e-7
start, end = 0, batch_size
# 开始迭代
for i in range(iter_count):
# 计算临时更新参数
w_temp = w - step * v
# 计算梯度
dw = np.sum((np.dot(data[start:end], w_temp) - y[start:end]) * data[start:end], axis=0).reshape((features + 1, 1)) / length
# 计算累积梯度平方
Sdw = beta * Sdw + (1 - beta) * np.dot(dw.T, dw)
# 计算速度更新量、
v = alpha * v + (1 - alpha) * dw
# 更新参数
w = w - (step / np.sqrt(eta + Sdw)) * v
start = (start + batch_size) % length
if start > length:
start -= length
end = (end + batch_size) % length
if end > length:
end -= length
return w
关于 RMSProp 相关的代码都可从 传送门 中获得。
参考
- 吴恩达老师的深度学习课程
- Deep Learning 最优化方法之 RMSProp:https://blog.csdn.net/bvl10101111/article/details/72616378