二分专项训练
写在前面——:
2016 9 28
二分也搞了快三天了,嘛,总结了一点东西,希望能对看官有用。
1、如果你是刚开始搞二分,首先要找个会打二分的人要个简单题的板子,自己学习学习,这很重要。
2、做题要看好是“最大值最小”还是“最小值最大”两者有着不同的判断方式。
3、判断函数里面 return的 if里的 等号的 加与不加 要想清楚,自己考虑考虑加或者不加等号是否会有更优的答案,(本博客里好几道题都很详细的写了 判断函数中等号的加与不加对答案的影响)。
4、对于 聪明的质检员 这种求绝对值之差最小的,使劲往给定值上凑就好了(不过这题需要前缀和优化,裸二分的话只能跑70)。
5、有些题,二分不是很难,难在其他地方上,(比如抄书系列,搞事!搞事!搞事!)
6、如果有的题是二分+SPFA,要尽可能的降低时间复杂度(SPFA时间复杂度玄学,有时候一个常数优化乘上SPFA就能大幅度降低时间复杂度,比如 收费站),比如读入优化,尽量还是根据题目的性质来降低时间复杂度。
7、NOIP要出二分的话,应该不会很难(毒奶),看看 聪明的质检员 和 跳石子就知道了。
—————————————————分割线————————————————
(2016 9 28 最近想把浮点数的题给补全…..)
2016 9 26
在openjudge水了一波…..
第一题:
在一个非降序列中,查找与给定值最接近的元素。
用lower_bound即可,太水没做….
第二题:
已知 f(1.5) > 0 , f(2.4) < 0 且方程 f(x) = 0 在区间 [1.5,2.4] 只有一个零点
该函数在区间[1.5,2.4]单调递减,完了;
第三题:
描述
平面上有一个大矩形,其左下角坐标(0,0),右上角坐标(R,R)。大矩形内部包含一些小矩形,小矩形都平行于坐标轴且互不重叠。所有矩形的顶点都是整点。要求画一根平行于y轴的直线x=k(k是整数) ,使得这些小矩形落在直线左边的面积必须大于等于落在右边的面积,且两边面积之差最小。并且,要使得大矩形在直线左边的的面积尽可能大。注意:若直线穿过一个小矩形,将会把它切成两个部分,分属左右两侧。
输入
第一行是整数R,表示大矩形的右上角坐标是(R,R) (1 <= R <= 1,000,000)。
接下来的一行是整数N,表示一共有N个小矩形(0 < N <= 10000)。
再接下来有N 行。每行有4个整数,L,T, W 和 H, 表示有一个小矩形的左上角坐标是(L,T),宽度是W,高度是H (0<=L,T <= R, 0 < W,H <= R). 小矩形不会有位于大矩形之外的部分。
输出
输出整数n,表示答案应该是直线 x=n。 如果必要的话,x=R也可以是答案。
我们需要记录一下每个矩形的横坐标,也就是lx和rx;
在判断的时候:
ll can(int x)
{
ll ansl=0;
ll ansr=0;
for(int i=1;i<=n;i++)
{
if(sz[i].rx<=x)
{
ansl+=(ll)(sz[i].rx-sz[i].lx)*sz[i].h;
}
else if(sz[i].lx>=x)
{
ansr+=(ll)(sz[i].rx-sz[i].lx)*sz[i].h;
}
else if(sz[i].lx<x&&x.rx)
{
ansl+=(ll)(x-sz[i].lx)*sz[i].h;
ansr+=(ll)(sz[i].rx-x)*sz[i].h;
}
}
return ansl-ansr;
} 最后二分完了还有一句….并且,要使得大矩形在直线左边的的面积尽可能大
于是:
if(abs(can(l))<=abs(can(r)))
printf("%d",l);
else
printf("%d",r);感觉问题不大了,但是还是死活WA了一个点….找Euk学长调了一会也没调出来。
厚颜无耻的9分代码:
#includex-sz[i].lx)*sz[i].h;
ansr+=(ll)(sz[i].rx-x)*sz[i].h;
}
}
return ansl-ansr;
}
void div()
{
int l=0,r=R;
int mid;
while(l<=r)
{
mid=(l+r)>>1;
ll hah=can(mid);
if(hah<=minans&&hah>0)
{
minans=min(minans,hah);
r=mid-1;
}
else
{
l=mid+1;
}
}
if(abs(can(l))<=abs(can(r)))
printf("%d",l);
else
printf("%d",r);
}
int main()
{
scanf("%d%d",&R,&n);
for(int i=1;i<=n;i++)
{
int w,h;
scanf("%d%d%d%d",&sz[i].lx,&sz[i].ly,&w,&h);
sz[i].h=h;
sz[i].rx=sz[i].lx+w;
minans+=(ll)w*h;
// printf("%d %d %d %d\n",sz[i].lx,sz[i].ly,h,sz[i].rx);
}
div();
return 0;
} 第四题:
没有思想难度,但要注意零的情况…..你要问为什么的话= =
第五题:
我的生日要到了!根据习俗,我需要将一些派分给大家。我有N个不同口味、不同大小的派。
有F个朋友会来参加我的派对,每个人会拿到一块派(必须一个派的一块,不能由几个派的小块拼成;
可以是一整个派)。我的朋友们都特别小气,如果有人拿到更大的一块,就会开始抱怨。
因此所有人拿到的派是同样大小的(但不需要是同样形状的),虽然这样有些派会被浪费,
但总比搞砸整个派对好。当然,我也要给自己留一块,而这一块也要和其他人的同样大小。
请问我们每个人拿到的派最大是多少?每个派都是一个高为1,半径不等的圆柱体。
输入
第一行包含两个正整数N和F,1 ≤ N, F ≤ 10 000,表示派的数量和朋友的数量。
第二行包含N个1到10000之间的整数,表示每个派的半径。
输出
输出每个人能得到的最大的派的体积,精确到小数点后三位。
样例输入
3 3
4 3 3
样例输出
25.133
这个题太水….没什么好说的,唯一注意的一点就是π的精度。
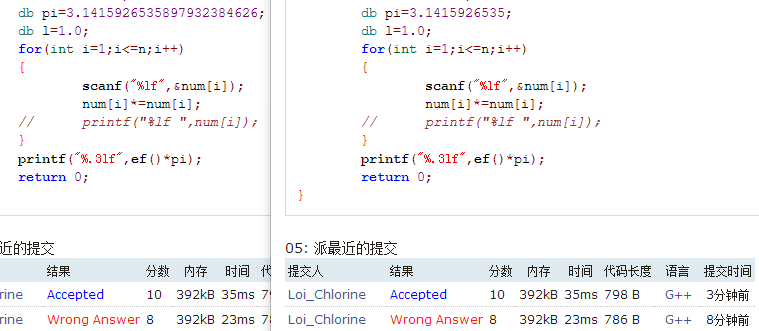
23333自己体会
第六题:
描述
农夫约翰是一个精明的会计师。他意识到自己可能没有足够的钱来维持农场的运转了。他计算出并记录下了接下来 N (1 ≤ N ≤ 100,000) 天里每天需要的开销。
约翰打算为连续的M (1 ≤ M ≤ N) 个财政周期创建预算案,他把一个财政周期命名为fajo月。每个fajo月包含一天或连续的多天,每天被恰好包含在一个fajo月里。
约翰的目标是合理安排每个fajo月包含的天数,使得开销最多的fajo月的开销尽可能少。
输入
第一行包含两个整数N,M,用单个空格隔开。
接下来N行,每行包含一个1到10000之间的整数,按顺序给出接下来N天里每天的开销。
输出
一个整数,即最大月度开销的最小值。
每次二分判断时记录每个fajo月的钱数为x,所得出的fajo月总数tot,如果tot<=m
说明当前的钱数如果减小的话可能会有更优的解(当tot==m时,说明当前的钱数完全可以组成m个fajo月,如果钱数加大的话,不会更优),用ans和当前的mid取个min
#include等等…这题我好像在哪见过
第七题:
描述
给出若干个整数,询问其中是否有一对数的和等于给定的数。
输入
共三行:
第一行是整数n(0 < n <= 100,000),表示有n个整数。
第二行是n个整数。整数的范围是在0到10^8之间。
第三行是一个整数m(0 <= m <= 2^30),表示需要得到的和。
输出
若存在和为m的数对,输出两个整数,小的在前,大的在后,中间用单个空格隔开。若有多个数对满足条件,选择数对中较小的数更小的。若找不到符合要求的数对,输出一行No。
小到大sort一边,从1–>n枚举,EF(i,i+1,n)表示当前的较小值为num[i],要找的另一个值所在的区间为[i+1,n],∵若有多个数对满足条件,选择数对中较小的数更小的。∴第一次找到的两个和为m的数,就是正解;
PS:puts(“No”); not puts(“NO”);
这题太水了= =;
#include1;
}
else if(num[hah]+num[mid]>m)
{
r=mid-1;
}
else if(num[hah]+num[mid]==m)
{
// printf("%d %d\n",num[hah],num[mid]);
minans=num[hah];
maxans=num[mid];
flag=1;
return true;
}
}
return false;
}
int main()
{
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
scanf("%d",&num[i]);
}
sort(num+1,num+n+1);
scanf("%d",&m);
for(int i=1;i<=n-1;i++)
{
if(num[i]+num[i+1]<=m)
{
if(div(i,i+1,n))
break;
}
else
break;
}
if(flag)
printf("%d %d",minans,maxans);
else
puts("No");
return 0;
}
/*07:和为给定数
总时间限制: 1000ms 内存限制: 65536kB
描述
给出若干个整数,询问其中是否有一对数的和等于给定的数。
输入
共三行:
第一行是整数n(0 < n <= 100,000),表示有n个整数。
第二行是n个整数。整数的范围是在0到10^8之间。
第三行是一个整数m(0 <= m <= 2^30),表示需要得到的和。
输出
若存在和为m的数对,输出两个整数,小的在前,大的在后,中间用单个空格隔开。
若有多个数对满足条件,选择数对中较小的数更小的。若找不到符合要求的数对,输出一行No。
样例输入
4
2 5 1 4
6
样例输出
1 5
查看*/ 第九题:
恶心到不行的一道浮点数…..如果是神犇的话就去随便A吧,反正NOIP不考浮点数…
第十题:
就是NOIP2015 D2T1原题
题目描述 Description
一年一度的“跳石头”比赛又要开始了!
这项比赛将在一条笔直的河道中进行,河道中分布着一些巨大岩石。组委会已经选择好了两块岩石作为比赛起点和终点。在起点和终点之间,有N块岩石(不含起点和终点的岩石)。在比赛过程中,选手们将从起点出发,每一步跳向相邻的岩石,直至到达终点。
为了提高比赛难度,组委会计划移走一些岩石,使得选手们在比赛过程中的最短跳跃距离尽可能长。由于预算限制,组委会至多从起点和终点之间移走M块岩石(不能移走起点和终点的岩石)。
输入描述 Input Description
输入文件名为 stone.in。
输入文件第一行包含三个整数L,N,M,分别表示起点到终点的距离,起点和终点之间的岩石数,以及组委会至多移走的岩石数。
接下来N行,每行一个整数,第i行的整数Di(0 < Di < L)表示第i块岩石与起点的距离。这些岩石按与起点距离从小到大的顺序给出,且不会有两个岩石出现在同一个位置。
输出描述 Output Description
输出文件名为stone.out。
输出文件只包含一个整数,即最短跳跃距离的最大值。
在判断函数里面记录一下当前最短跳跃距离为x时,需要移走的石头总数tot,
当tot<=m时说明当前的x过小,x需要增大(当tot==m时,x越大会让解更优);
让ans和当前的mid取个max
#include2016 9 29
除了第一题太水…..第三题9分没调出来,第九题太恶心以外…NOI OPENJUDGE 上的二分已经刷完了
接下来就是愉快的codevs二分时间了~
CODEVS 1138 聪明的质zhang检qvan员dan
CODEVS 4175 收费站
CODEVS 2072 分配房间
CODEVS 2744 养鱼喂妹纸
CODEVS 抄书问题系列
BOSS战 CODEVS 1183 泥泞的道路