【CodeForces 611C】一维+二维前缀和 | 容斥原理 | 动态规划 | E

                                611C. New Year and Domino

                                                                         time limit per test: 3 seconds

                                                                  memory limit per test: 256 megabytes

URL

https://codeforces.com/contest/611/problem/C

 

 

Introduction

给出一个矩形区域，上面有一些点或者#号，点代表空位，#号代表已被占用。

现在有一个 1×2 的条形物品需要放进去，所以只能放在相邻的两个空位里。

多次询问，每次给出一个子矩形的 左上角 和 右下角 的行列坐标，问在这个矩形范围内部一共有多少种放置可能。（是在内部！也就是说只放一半在这个矩形区域中的方案数不算！）

 

Input

一组输入。第一行输入行数 R 和列数 C（范围 [1, 500] ），

接下来 R 行，每行一个仅由 '.'  或 '#' 组成的字符串，

再输入一个数 q，代表有 q 次询问，

接下来 q 行，每行两对点的行列坐标 r1 c1 r2 c2 （1 ≤ r1 ≤ r2 ≤ R, 1 ≤ c1 ≤ c2 ≤ C)。

 

Output

对于每次询问，输出在此范围内的可能放置种数。

 

Sample Input

5 8
....#..#
.#......
##.#....
##..#.##
........
4
1 1 2 3
4 1 4 1
1 2 4 5
2 5 5 8
 

Sample Output

4
0
10
15

第一次询问  答案是4  图解：

 

 

Analysis

看到此题，二维dp 的思路应该马上就会涌出。那具体如何dp呢？这里需要借鉴 二维前缀和 的思想。

也就是在二重循环的时候，状态转移的进行就是像计算二维矩阵前缀和那样，由其上方的矩形和左边的矩形 转移到当前的大矩形（当然还会涉及到左上角的重叠小矩形）

 

1. 【dp定义】： dp[r][c] 表示 由第1行、第r行 、第1列、第c列 围成的矩形区域 内部 的摆放方案数（应题：注意是内部方案数，也就是不包括跨越此区域边界放置的情况！）

2. 【dp初始化】：dp[0][...] = 0, dp[...][0] = 0（我们让行列数从1开始数起，这是一个计算二维前缀和时常用的小技巧，这样就不用在做减法的时候担心越界以及担心减去的不是0了）

3. 【dp顺序】：外层循环行，内层循环列

4. 【状态转移方程】：

   1. dp[r][c] = dp[r-1][c] + dp[r][c-1] - dp[r-1][c-1] （利用 二维前缀和 的思想）

   2. if (a[r][c] == '.' && a[r][c-1] == '.')  ++dp[r][c] 

   3. if (a[r][c] == '.' && a[r-1][c] == '.')  ++dp[r][c] 

好，重点来了，状态转移方程为什么是这样的？是怎么来的？分析如下：

首先，朴素二维前缀和的状态转移方程相当于是 dp[r][c] = n[r][c] + dp[r-1][c] + dp[r][c-1] - dp[r-1][c-1]，但这道题并不是二维前缀和。

他们的主要差别在于：

1. 上式中的 n[r][c] 在二维前缀和中代表矩阵对应位置的元素值，那在本题是表示什么？
2. （ 关键 ）本题的 放置 会涉及到 两个相邻格子，那这样还能用二维前缀和的思想吗？上面写的那三步状态转移方程就能够不重不漏地得到当前方案数吗？

 

这两个差别带来的问题其实不难解决。我们需要的只是简单画一张图，然后一切都明了了：

 

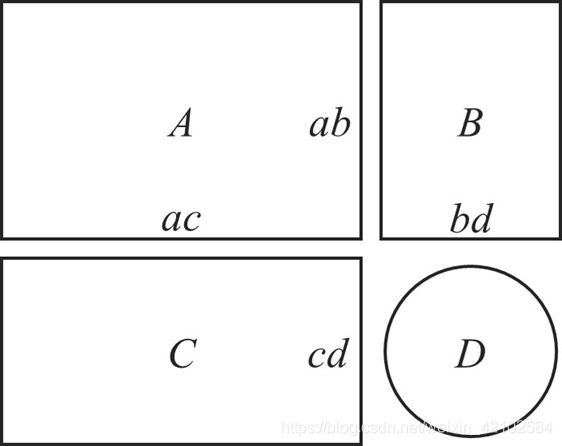
如上图，记 A、B、C 分别表示三个矩形区域 内部 的放置种数。【注意】是内部放置种数！也就是说不包括跨边界的放置情况！（再次强调应题）

记 D 代表我们当前遍历到的那一个格子，它在 r 行 c 列

记 ab、bd、cd、ac 分别表示四个交界处产生的 跨边界 放置种数。【注意】这里才是跨边界的放置情况

比如 ab 的值就是在 A、B区域 相邻的两列 放置物品的可能种类数（物品一半放在A中，一半放在B中）。其他的同理。

 

所以，根据我们的 dp定义（内部方案数），就可以很明确地得到，我们想求的 dp[r][c] == A + B + C + ab + bd + cd + ac

再根据dp定义看看 dp[r-1][c] 是什么：dp[r-1][c] == A + ab + B。同理，dp[r][c-1] == A + ac + C，dp[r-1][c-1] == A

将上一行的三个等式带入我们的状态转移方程第一步的右边，得到 右边（即dp[r-1][c] + dp[r][c-1] - dp[r-1][c-1]）== A + ab + B + A + ac + C - A == A + B + C + ab + ac

再看这个结果和 dp[r][c] 差什么？差的就是 bd 和 cd。

那 bd 和 cd 怎么求呢？因为 D 就是一个点，所以很简单：如果 D 这个点和它上面相邻的点都是空位的话，bd就是1，否则就是0.

同理，如果 D 和它左边相邻的点都是空位的话，cd就是1，否则就是0.

所以我们得到了完整的状态转移方程：

            dp[r][c] = dp[r-1][c] + dp[r][c-1] - dp[r-1][c-1];

            if (D和它上面的点都是空位)  dp[r][c] += 1;（加的就是bd）

            if (D和它左边的点都是空位)  dp[r][c] += 1;（加的就是cd）

这也就是我们上面那三步状态转移方程由来。整个 dp 过程显然在 Θ(R*C) 内完成。

 

 

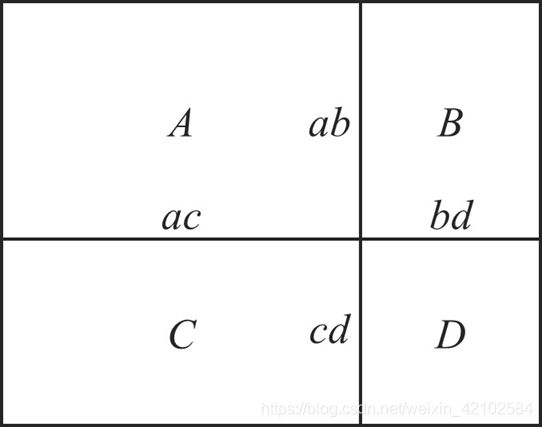
那么每次询问的答案是什么呢？这个也好办，我们把图稍微改改，把 D 改成我们查询的区域（D左上角是(r1, c1)，右下角是(r2, c2)）：

 

这样的话，显然有：

dp[r2][c2] == A + B + C + D + ab + bd + cd + ac （就是全部加起来嘛）

dp[r1-1][c2] == A + ab + B

dp[r2][c1-1] == A + ac + C

dp[r1-1][c1-1] == A

所以有：

借鉴 容斥原理（二维前缀和加加减减）：

  dp[r2][c2] + dp[r1-1][c1-1] - dp[r1-1][c2] - dp[r2][c1-1] == A + B + C + D + ab + bd + cd + ac + A - (A + ab + B) - (A + ac + C)

== D + cd + bd

所以我们拿 dp[r2][c2] + dp[r1-1][c1-1] - dp[r1-1][c2] - dp[r2][c1-1] 的结果再减去 cd 和 bd 就得到我们的查询结果 D 了。

那 cd 和 bd 怎么求呢？cd 的意义其实是C区和D区相邻两列之间可能的放置总数。这个就可以用 一维前缀和 求了。维护一个 left[r][c] 表示在第 c 列中、从第 1 行到第 r 行这个范围内有多少个格子它自己和它左边相邻格子都是空位。bd同理可求，维护一个up[r][c]即可。

 

 

综上，我们就可以得到查询结果应该是：

ans = (dp[r2][c2] + dp[r1-1][c1-1] - dp[r1-1][c2] - dp[r2][c1-1])(加加减减) - (left[r2][c1] - left[r1-1][c1])(cd) - (up[r1][c2] - up[r1][c1-1])(bd)

每次查询在 O(1) 内完成

 

矩阵长宽记为R、C，询问次数记为q，总时间复杂度 Θ(R*C + q)，最大操作数量级 1e5 可接受。空间复杂度 Θ(R*C)。

 

AC Code

#include 

#define _F0N(i,n) for(i=0;i57;_c=getchar())if(_c==45)_v=-1;for(;_c>=48&&_c<=57;x=(x<<1)+(x<<3)+_c-48,_c=getchar());x*=_v;}
#define PC putchar
templatevoid PRT(const T a){if(a<0){PC(45),PRT(-a);return;}if(a>=10)PRT(a/10);PC(a%10+48);}
templatevoid UPRT(const T a){if(a>=10)PRT(a/10);PC(a%10+48);}

#define CON constexpr
#define T_CASE int _CASE;sc(_CASE)for(int __=1;__<=_CASE;++__)
#define cincout cin.tie(0),ios::sync_with_stdio(false)
#define eps 1e-8
#define PI 3.141592653589793
#define MAX_INT 2147483647
#define MAX_LL 9223372036854775807
#define INF 0x3f3f3f3f
#define LINF 0x3f3f3f3f3f3f3f3fLL
#define endl '\n'
#define priority_queue priority_queue
#define PQ std::priority_queue
#define PR std::pair
#define vector vector
#define VI std::vector
#define MII std::map
#define MLI std::map
#define MSI std::map
#define PII std::pair
#define PLI std::pair
#define PSI std::pair
#define MPFD(k) auto it=mp.find(k)

#define MIN(a, b) ((a)<(b)?(a):(b))
#define MIN3(a, b, c) (MIN(a, MIN(b, c)))
#define MAX(a, b) ((a)>(b)?(a):(b))
#define MAX3(a, b, c) (MAX(a, MAX(b, c)))
#define get_max(a,l,r,_max) auto _max=a[l];for(int _i=l+1,_r=r;_i<_r;++_i)if(_maxa[_i])_min=a[_i]
#define ABS(a) (a>0?a:-a)
#define FABS(a) (a>0?a:-a)
#define log2n(x) (log(x)/0.69314718055995)

#define PB emplace_back
#define EB emplace_back
#define EK else break
#define ALL(X) (X).begin(),(X).end()
#define SORT(X) std::sort(ALL(X))
#define SORTD(X) std::sort(ALL(X),std::greater())
#define swap(a, b) do{auto _t=a; a=b; b=_t;}while(0)
#define mem0(a) memset(a,0,sizeof(a))
#define memf1(a) memset(a,-1,sizeof(a))
#define meminf(a) memset(a,0x3f,sizeof(a))

CON int MN(503);

char a[MN][MN];
int dp[MN][MN];
int lf[MN][MN], up[MN][MN];

void dpd(const int R, const int C)
{
	for (int r=1; r<=R; ++r)
	{
		for (int c=1; c<=C; ++c)
		{
			dp[r][c] = dp[r-1][c] + dp[r][c-1] - dp[r-1][c-1];
			lf[r][c] += lf[r-1][c];
			up[r][c] += up[r][c-1];

			if (a[r][c] == '.' && a[r][c-1] == '.')
				++lf[r][c], ++dp[r][c];
			if (a[r][c] == '.' && a[r-1][c] == '.')
				++up[r][c], ++dp[r][c];
		}
	}
}

int main()
{
	get(R, C)
	for (int r=1; r<=R; ++r)
		scanf("%s", a[r]+1);

	dpd(R, C);

	get(q)
	while (q--)
	{
		get(r1, c1)get(r2, c2)

		int ans = dp[r2][c2] + dp[r1-1][c1-1] - dp[r1-1][c2] - dp[r2][c1-1];
		ans -= lf[r2][c1] - lf[r1-1][c1];
		ans -= up[r1][c2] - up[r1][c1-1];

		UPRT(ans), PC(10);
	}

	return 0;
}

 

加油！