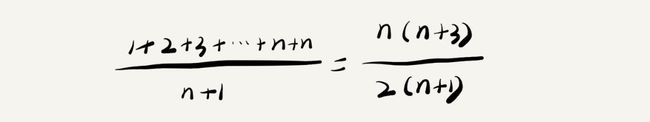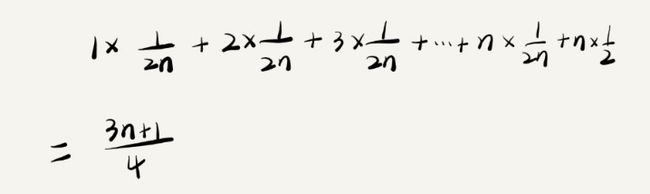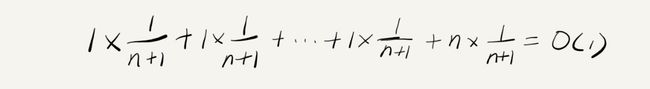重拾算法之复杂度分析(大O表示法)
在论坛里经常会看到一句话:学不会算法就去做网页开发。当然,从某种层面来看,前端对算法的要求确实不高,毕竟想写一个级联选择器会找到一大把的组件库。但是呢,算法又是一个优秀的工程师必须具备的的基础内功。程序员之间流传这么一句话:“一流程序员靠数学,二流靠算法,三流靠逻辑,四流靠SDK,五流靠Google和StackOverFlow,六流靠百度和CSDN。低端的看高端的就是黑魔法!”。对于面试一些大公司而言,尤其是国外的互联网企业,算法也是绕不过的一道坎。大学时买过一本很厚的算法书《算法导论》,翻开书当时就被里面的高等数学吓退了,后来也再也没看过。对于算法初学者来讲,看《算法导论》、《计算机程序设计艺术》这样的算法圣经不是很好的途径,所以我决定从一些简单的书籍像《算法图解》、《数学之美》以及王争(前google工程师)的付费专栏《数据结构与算法之美》开始算法学习,代码主要以javascript为主,可能会穿插C语言,如果有精力刷题,可能会加入一些我认为有趣的leetcode算法题。学习笔记也会在博客一直更新,希望能做一个相对完整的更新。
复杂度分析,会贯穿整个算法学习过程中。王争说,掌握了复杂度分析,就掌握了算法学习的一半。因此,今天我们来聊复杂度分析——大O复杂度表示法。
一个简单的公式
引用算法图解一个有趣的例子:Bob要写一个算法计算月球登陆前执行帮助计算着陆点的算法,他用两种算法:简单查找跟二分查找。假设查找一个元素要1ms,查找100的元素简单查找要100ms,二分查找只需要检查7个元素( log2(7)),大概7ms。而如果要查找10亿个元素,用二分查找就是30ms左右,简单查找却要10亿毫秒。为什么会这样呢?因为两种算法运行时间的增速不同。在高中数学中学概率问题都是基于大量数据统计,同样,估算算法的执行效率,也是基于对运行时间与数据的渐进式增长的粗略分析,我们的大O表示法该登场了!
假设每个语句执行时间为t,则以下代码:
function sum (){
let sum = 0; /*执行时间t*/
let i = 0; /*执行时间t*/
let j = 0; /*执行时间t*/
for(; i < n; i++){ /*执行时间n*t */
j = 1; /*执行时间n*t*/
for(; j < n; j++){ /*执行时间n的平方*t*/
sum = sum + i * j; /*执行时间n的平方*/
}
}
}
整段代码整的执行时间为: T(n) = (2n²+2n+3)*t ,所有代码的执行时间T(n)与每行代码的执行次数成正相关!大O表示法计算的并不是代码的正式运行时间,而是代码执行时间随数据规模增长的变化趋势,即 时间复杂度。
时间复杂度分析
1. 只关注循环执行次数最多的一段代码
在分析代码复杂度的时候,只关注循环执行次数最多的那一段代码就可以,如下代码:
function cal(n) {
let sum = 0;
for (let i = 0; i <= n; i++) {
sum = sum + i;
}
return sum;
}
上述代码我们只需要关注for循环代码执行次数n,所以中的时间复杂度为O(n)。
2. 加法法则:总复杂度等于量级最大的那段代码的复杂度
我们回到这篇文章的第一段代码,该代码中的执行时间为 T(n) = (2n²+2n+3)*t ,所以量级最大的那段代码运行时间为n的平方,则这段代码的时间复杂度为:O(n²).
3. 乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
function cal(n) {
let ret = 0;
for (let i + 0; i < n; i++) {
ret = ret + f(i);
}
}
function f(n) {
int sum = 0;
for (let i = 0; i < n; i++) {
sum = sum + i;
}
return sum;
}
以上代码在cal函数中嵌套f函数,cal函数不看f,时间复杂度为O(n),f函数的时间复杂度为O(n),整个cal函数的时间复杂度为O(n²)。
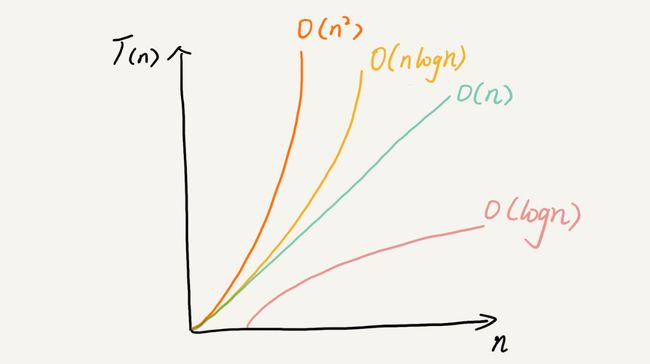
常见的时间复杂度量级
1. O(1)
let i = 8; /* 时间复杂度: O(1) */
let j = 6; /* 时间复杂度: O(1) */
let sum = i + j; /* 时间复杂度: O(1) */
2. O(logn)、O(nlogn)
let i = 1;
while (i < = n) {
i = i * 2;
}
上述代码,当i = 1时,进入while后,i 赋值为2,下一次赋值为4,依次指数增长,那么他在while中执行的次数为log2(n),忽略系数,则时间复杂度为O(logn)。在排序中如归并排序,快速排序的时间复杂度为O(nlogn)。
1. O(m+n)、O(m*n)
int cal(int m, int n) {
int sum_1 = 0;
int i = 1;
for (; i < m; ++i) {
sum_1 = sum_1 + i;
}
int sum_2 = 0;
int j = 1;
for (; j < n; ++j) {
sum_2 = sum_2 + j;
}
return sum_1 + sum_2;
}
上述代码的复杂度为 m + n。
4. O(n2)----选择排序
5. O(n!)
著名的旅行商问题,有一位旅行商,要去5个城市,要求找出路程总和最少的路线,我们只能把所有可能的路线可能5!= 120中方法算一遍来找出,这是计算机领域无最优解的问题。
空间复杂度
空间复杂度全称就是渐进空间复杂度,表示算法的存储空间与数据规模之间的增长关系。此处不做详细说明。
不同的大O运行时间
1. 最好情况时间复杂度与最坏时间复杂度
// n 表示数组 array 的长度
function find(array, n, x) {
let pos = -1;
for ( let i = 0; i < n; i++) {
if (array[i] == x) {
pos = i;
break;
}
}
return pos;
}
在一个长度为n的数组中找一个数,如果在遍历第一次就找到,则时间复杂度为O(1),如果整个数组遍历了一遍,那么时间复杂度为O(n)。
最好情况时间复杂度就是,在最理想的情况下,执行这段代码的时间。最坏情况时间复杂度就是,在最糟糕的情况下,执行这段代码的时间。
2. 平均情况时间复杂度
高中时,我们都学过数学期望,平均时间复杂度的实质就是数学期望。
以上代码中,查找X在数组中的位置有n+1中情况,即在0~n-1或者不在数组中,把查找的每种情况遍历的元素除以查找次数,就是遍历元素的平均值。
忽略系数,则时间复杂度为O(n)。但是,在概率统计中,查找元素时,要么可以查找到,要么差找不到,我们假设他们的概率各位一半,那么计算如下:
最终得到的时间复杂度为O(n)。
3. 均摊时间复杂度
/* array 表示一个长度为 n 的数组
代码中的 array.length 就等于 n */
let array = new Array[n];
function insert(val) {
if (count == array.length) {
let sum = 0;
for (let i = 1; i < array.length; i++) {
sum = sum + array[i];
}
array[0] = sum;
count = 1;
}
array[count] = val;
count++;
}
以上代码有两种情况:
-
当count不等于数组长度时,每次调用函数的时候,时间复杂度为O(1),这种情况出现的次数为n次;
-
当count等于数组长度时,调用函数时,走进for循环,此时时间复杂度为:O(n)
-
该例子较上面的例子的特殊之处在于,函数在大多数情况下的时间复杂度为O(1),而当最坏时间复杂度的时候出现的几率很小,这时候我们需要引入一种分析的方法叫:摊还分析法,通过该分析法得到的时间复杂度为均摊时间复杂度。
在上面的例子里,每一次O(n)的插入都会有n-1次时间复杂度为O(1)的插入,我们吧耗时多的这次的操作均摊到n-1次耗时少的上面,实际的均摊复杂度就为O(1)。
均摊复杂度的出现情况很少,可以把它认为是一种特殊的平均时间复杂度。它的应用场景都是在一系列连续操纵中,大部分情况复杂度低,个别复杂度高,这时候就可以平摊下来。而且,一般情况下,在能够应用均摊时间复杂度分析的场合,一般均摊时间复杂度就等于最好情况时间复杂度。
参考文档:
1: 王争(前google工程师)专栏 ----《数据结构与算法之美》
2: 《算法图解》------大O表示法部分