用 Python 绘制音乐图谱

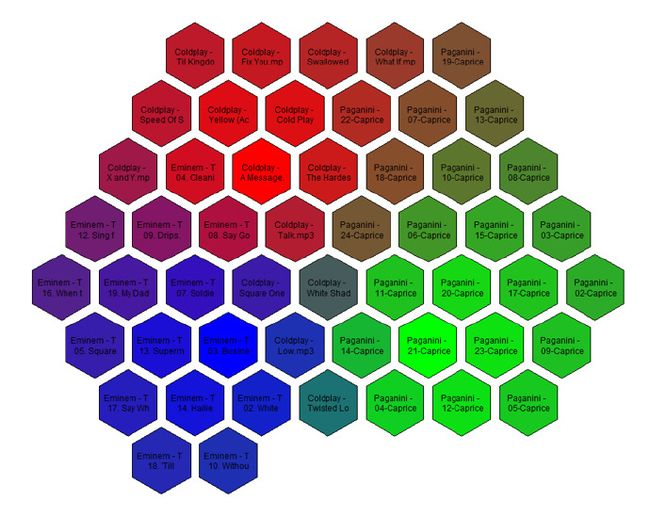
在本文中，我们将探讨一种简洁的方式，以此来可视化你的MP3音乐收藏。此方法最终的结果将是一个映射你所有歌曲的正六边形网格地图，其中相似的音轨将处于相邻的位置。不同区域的颜色对应不同的音乐流派（例如：古典、嘻哈、重摇滚）。举个例子来说，下面是我所收藏音乐中三张专辑的映射图：Paganini的《Violin Caprices》、Eminem的《The Eminem Show》和Coldplay的《X&Y》。

为了让它更加有趣（在某些情况下更简单），我强加了一些限制。首先，解决方案应该不依赖于MP3文件中任何已有的ID3标签（例如，Arist，Genre），应该仅仅使用声音的统计特性来计算歌曲的相似性。无论如何，很多我的MP3文件标记都很糟糕，但我想使得该解决方案适用于任何音乐收藏文件，不管它们的元数据是多么糟糕。第二，不应使用其他外部信息来创建可视化图像，需要输入的仅仅是用户的MP3文件集。其实，通过利用一个已经被标记为特定流派的大型歌曲数据库，就能提高解决方案的有效性，但是为了简单起见，我想保持这个解决方案完全的独立性。最后，虽然数字音乐有很多种格式（MP3、WMA、M4A、OGG等），但为了使其简单化，这里我仅仅关注MP3文件。其实，本文开发的算法针对其他格式的音频也能很好地工作，只要这种格式的音频可以转换为WAV格式文件。

创建音乐图谱是一个很有趣的练习，它包含了音频处理、机器学习和可视化技术。基本步骤如下所示：

1. 转换MP3文件为低比特率WAV文件。
2. 从WAV元数据中提取统计特征。
3. 找到这些特征的一个最佳子集，使得在这个特征空间中相邻的歌曲人耳听起来也相似。
4. 为了在一个XY二维平面上绘图，使用降维技术将特征向量映射到二维空间。
5. 生成一个由点组成的六角网格，然后使用最近邻技术将XY平面上的每一首歌曲映射六角网格上的一个点。
6. 回到原始的高维特征空间，将歌曲聚类到用户定义数量的群组中（k=10能够很好地实现可视化目的）。对于每个群组，找到最接近群组中心的歌曲。
7. 在六角网格上，使用不同的颜色对k个群组中心的那首歌曲着色。
8. 根据其他歌曲在XY屏幕上到每个群组中心的距离，对它们插入不同的颜色。

下面，让我们共同看看其中一些步骤的详细信息。

MP3文件转换成WAV格式

将我们的音乐文件转换成WAV格式的主要优势是我们可以使用Python标准库中的“wave”模块很容易地读入数据，便于后面使用NumPy对数据进行操作。此外，我们还会以单声道10kHz的采样率对声音文件下采样，以使得提取统计特征的计算复杂度有所降低。为了处理转换和下采样，我使用了众所周知的MPG123，这是一个免费的命令行MP3播放器，在Python中可以很容易调用它。下面的代码对一个音乐文件夹进行递归搜索以找到所有的MP3文件，然后调用MPG123将它们转换为临时的10kHz WAV文件。然后，对这些WAV文件进行特征计算（下节中讨论）。

Python

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53

import subprocess import wave import struct import numpy import csv import sys   def read_wav ( wav_file ) :      """Returns two chunks of sound data from wave file."""      w = wave . open ( wav_file )      n = 60 * 10000      if w . getnframes ( ) < n * 2 :          raise ValueError ( 'Wave file too short' )      frames = w . readframes ( n )      wav_data1 = struct . unpack ( '%dh' % n , frames )      frames = w . readframes ( n )      wav_data2 = struct . unpack ( '%dh' % n , frames )      return wav_data1 , wav_data2   def compute_chunk_features ( mp3_file ) :      """Return feature vectors for two chunks of an MP3 file."""      # Extract MP3 file to a mono, 10kHz WAV file      mpg123_command = '..mpg123-1.12.3-x86-64mpg123.exe -w "%s" -r 10000 -m "%s"'      out_file = 'temp.wav'      cmd = mpg123_command % ( out_file , mp3_file )      temp = subprocess . call ( cmd )      # Read in chunks of data from WAV file      wav_data1 , wav_data2 = read_wav ( out_file )      # We'll cover how the features are computed in the next section!      return features ( wav_data1 ) , features ( wav_data2 )   # Main script starts here # =======================   for path , dirs , files in os . walk ( 'C:/Users/Christian/Music/' ) :      for f in files :          if not f . endswith ( '.mp3' ) :              # Skip any non-MP3 files              continue          mp3_file = os.path . join ( path , f )          # Extract the track name (i.e. the file name) plus the names          # of the two preceding directories. This will be useful          # later for plotting.          tail , track = os.path . split ( mp3_file )          tail , dir1 = os.path . split ( tail )          tail , dir2 = os.path . split ( tail )          # Compute features. feature_vec1 and feature_vec2 are lists of floating          # point numbers representing the statistical features we have extracted          # from the raw sound data.          try :              feature_vec1 , feature_vec2 = compute_chunk_features ( mp3_file )          except :              continue

特征提取

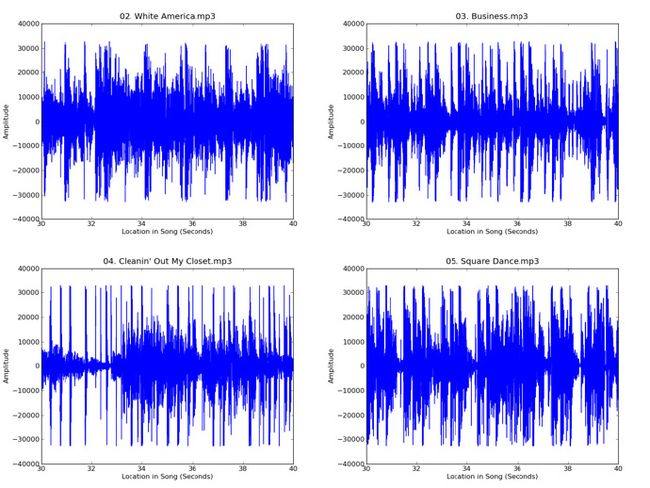
在Python中，一个单声道10kHz的波形文件表示为一个范围为-254到255的整数列表，每秒声音包含10000个整数。每个整数代表歌曲在对应时间点上的相对幅度。我们将分别从两首歌曲中分别提取一段时长60秒的片段，所以每个片段将由600000个整数表示。上面代码中的函数“read_wav”返回了这些整数列表。下面是从Eminem的《The Eminem Show》中一些歌曲中提取的10秒声音波形图：

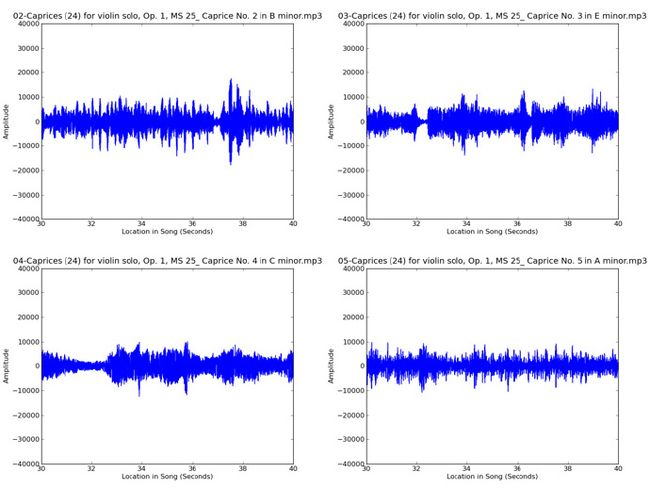
为了对比，下面是Paganini的《Violin Caprices》中的一些片段波形图：

从上面两个图中可以看出，这些片段的波形结构差别很明显，但一般来看Eminem的歌曲波形图看起来都有些相似，《Violin Caprices》的歌曲也是这样。接下来，我们将从这些波形图中提取一些统计特征，这些特征将捕捉到歌曲之间的差异，然后通过这些歌曲听起来的相似性，我们使用机器学习技术将它们分组。

我们将要提取的第一组特征集是波形的统计矩（均值、标准差、偏态和峰态）。除了对幅度进行这些计算，我们还将对递增平滑后的幅度进行计算来获取不同时间尺度的音乐特性。我使用了长度分别为1、10、100和1000个样点的平滑窗，当然可能其他的值也能取得很好的结果。

分别利用上面所有大小的平滑窗对幅度进行相应计算。为了获取信号的短时变化量，我还计算了一阶差分幅度（平滑过的）的统计特性。

上面的特征在时间域给出了一个相当全面的波形统计总结，但是计算一些频率域的特征也是有帮助的。像嘻哈这种重低音音乐在低频部分有更多的能量，而经典音乐在高频部分占有更多的比例。

将这些特征放在一起，我们就得到了每首歌曲的42种不同特征。下面的Python代码从一系列幅度值计算了这些特征：

选择一个最优的特征子集

我们已经计算了42种不同的特种，但是并不是所有特征都有助于判断两首歌曲听起来是否相同。下一步就是找到这些特征的一个最优子集，以便在这个减小的特征空间中两个特征向量之间的欧几里得距离能够很好地对应两首歌听起来的相似性。

变量选择的过程是一个有监督的机器学习问题，所以我们需要一些训练数据集合，这些训练集能够引导算法找到最好的变量子集。我并非通过手动处理音乐集并标记哪些歌曲听起来相似来创建算法的训练集，而是使用了一个更简单的方法：从每首歌曲中提取两段时长为1分钟的样本，然后试图找到一个最能匹配同一首歌曲中的两个片段的算法。

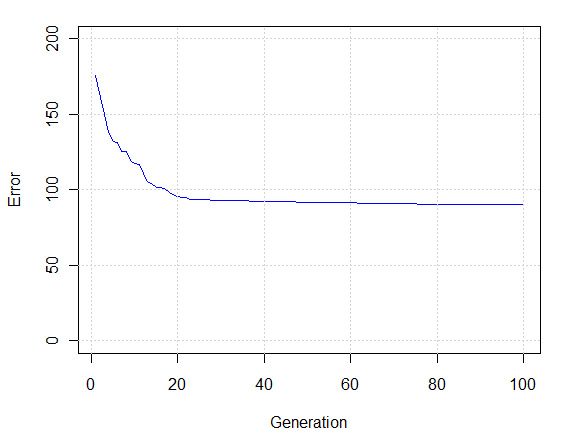
为了找到针对所有歌曲能够达到最好平均匹配度的特征集，我使用了一个遗传算法（在R语言的genalg包中）对42个变量中的每一个进行选取。下图显示了经过遗传算法的100次迭代，目标函数的改进情况（例如，一首歌的两个样本片段通过最近邻分类器来匹配到底有多么稳定）。

如果我们强制距离函数使用所有的42个特征，那么目标函数的值将变为275。而通过正确地使用遗传算法来选取特征变量，我们已经将目标函数（例如，错误率）减小到了90，这是一个非常重大的改进。最后选取的最优特征集包括：

• amp10mean
• amp10std
• amp10skew
• amp10dstd
• amp10dskew
• amp10dkurt
• amp100mean
• amp100std
• amp100dstd
• amp1000mean
• power2
• power3
• power4
• power5
• power6
• power7
• power8
• power9

在二维空间可视化数据

我们最优的特征集使用了18个特征变量来比较歌曲的相似性，但是我们想最终在2维平面上可视化音乐集合，所以我们需要将这个18维的空间降到2维，以便于我们绘画。为了实现这个目的，我简单地使用了前两个主成分来作为X和Y坐标。当然，这会引入一些错误到可视化图中，可能会造成一些在18维空间中相近的歌曲在2维平面中却不再相近。不过，这些错误无可避免，但幸好它们不会将这种关系扭曲得太厉害—听起来相似的歌曲在2维平面上仍然会大致集聚在一起。

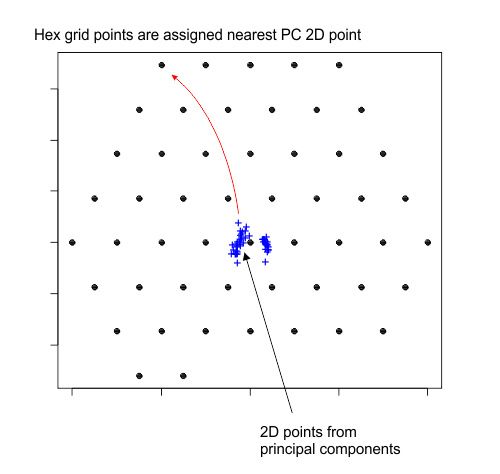
将点映射到一个六角网格

从主成分中生成的2D点在平面上不规则地分布。虽然这个不规则的分布描述了18维特征向量在2维平面上最“准确”的布置，但我还是想通过牺牲一些准确率来将它们映射到一个很酷的画面上，即一个有规律间隔的六角网格。通过以下操作实现：

1. 将xy平面的点嵌入到一个更大的六角网格点阵中。
2. 从六角形最外层的点开始，将最近的不规则间隔的主成分点分配给每个六角网格点。
3. 延伸2D平面的点，使它们完全填充六角网格，组成一个引人注目的图。

 

为图上色

这个练习的一个主要目的是不对音乐集的内容做任何假设。这意味着我不想将预定义的颜色分配给特定的音乐流派。相反，我在18维空间中聚合特征向量以找到聚集听起来相似的音乐的容器，并将颜色分配给这些群组中心。结果是一个自适应着色算法，它会找出你所要求的尽可能多的细节（因为用户可以定义群组的数量，也即是颜色数量）。正如前面提到的，我发现使用k=10的群组数量往往会给出好的结果。

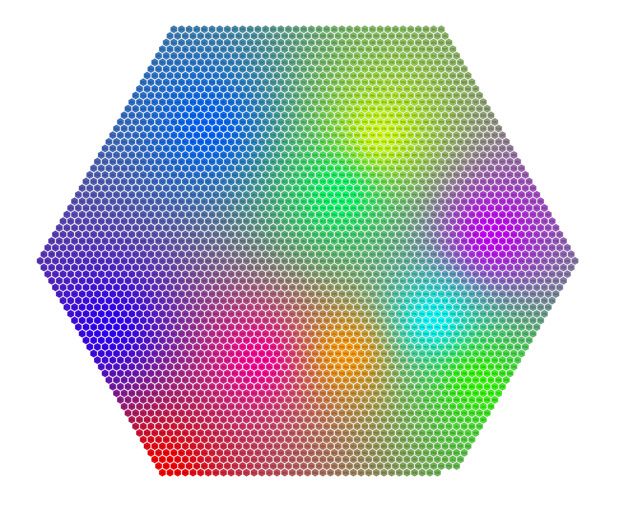
最终输出

为了娱乐，这里给出我音乐集中3668首歌曲的可视化图。全分辨率图片可以从这里获得。如果你放大图片，你将会看到算法工作的相当好：着色的区域对应着相同音乐流派的音轨，并且经常是相同的艺术家，正如我们希望的那样。