统计分析【一】—— 描述性统计实现

一、数据统计量描述

1、集中度描述

1.1 均值

1）描述
一组数据的算术平均，反应一组数据的集中分布趋势，缺点是容易受极端值影响。
2）公式

1.2 众数

一组数据中出现次数最多的数字，可能不止一个，可能没有。适用于当数据具有明显集中趋势的情况。

1.3 中位数

一组数据从小到大排列，位于中间的数据，其中偶数个数的数据为中间两个数据的算术平均，缺点是数据不敏感。

2、离散度描述

2.1 极差

最大值-最小值，反应一组数据的范围大小，极差越大越分散。

2.2 方差

1）描述
反应数据的离散程度，用来度量随机变量与期望的偏差程度。
2）总体方差

2.3 标准差

1）描述
反应数据的分散程度，为方差的算术平方根。
2）公式

2.4 变异系数

1）变异系数 = 标准偏差/平均数。
2）当需要比较两组数据的离散程度，但是两组数据量级大小不一致时，可以通过变异系数消除测量尺度带来的影响，但是不适用于平均值较小（接近0）的情况，会带来比较大的误差。
3）变异系数越大，数据越离散。
4）一般来讲，变异系数超过15%则考虑数据异常。

2.5 贝塞尔校正

在类似正态分布中，样本围绕在均值附近，抽取到边缘值的概率较小，样本值会偏向集中，因此计算出来的样本方差会较小，如果以此来估计整体方差时，需要进行适当放大，即除数修正为N-1。

二、数据处理工具

根据总体样本的大小进行处理的工具有多种，一般数据量级较少时采用EXCEL即可满足需求，数量级较大时（百万级别以上）一般采用SQL、R、python进行处理，须知方法只是作为满足需求的处理工具，一切以满足需要的便捷性出发，无需拘泥于工具本身。

1、EXCEL 函数

1.1、说明
采用 office Excel函数计算及数据分析功能。
1.2、实现

//平均值
=AVERAGE(数据区域)

//众数 数值型
=MODE(数据范围)

//众数文本型
=INDEX(数据范围,MAX(MATCH(数据范围,数据范围,数据范围,)))

//中位数
=MEDIAN(数据范围)

//极差 
=MAX(数据范围)-MIN（数据范围）

//方差
=VAR(数据范围)

//标准差
=STDEV(数据范围)

//变异系数
=STDEV(数据范围)/AVERAGE(数据区域)

2、EXCEL描述统计

1）功能开启

功能开启：文件 -》选项 -》加载项 -》转到 -》分析工具库

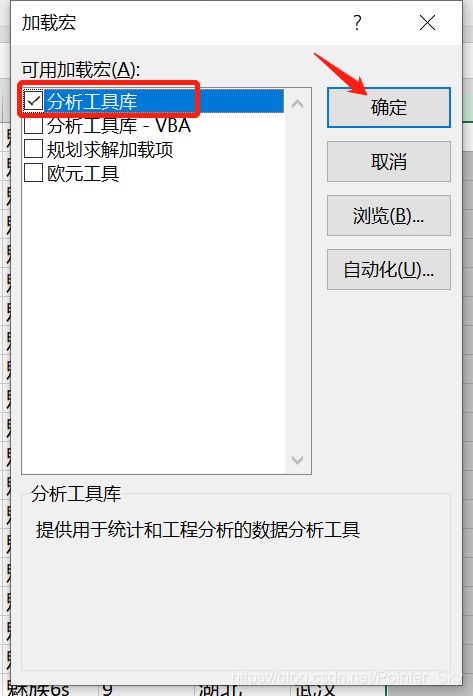
2）数据分析-描述统计
如果选择EXCEL的数据分析 -》描述统计功能，则可以一次性将以上所有指标一次性统计输出

3、SQL

3.1、说明
采用MYSQL及Navicat。
3.2、实现

//平均数
SELECT AVG(列名) FROM 表名

//众数
SELECT 列名,count(列名) as n
FROM 表名
GROUP BY 列名
HAVING n >=
(SELECT max(n)		
FROM (SELECT COUNT(列名) as n
			FROM 表名
			GROUP BY 列名)as tmp);
			
//中位数
SELECT AVG(DISTINCT 列名) 
FROM (SELECT T1.列名
from 表名 T1,表名 T2
GROUP BY T1.列名
HAVING 
sum(CASE WHEN T2.列名>= T1.列名 THEN 1 ELSE 0 END) >= count(*)/2
and
sum(case WHEN T2.列名<= T1.列名 then 1 else 0 end) >=count(*)/2) tmp

//极差
SELECT max(列名),min(列名),(max(列名)-min(列名)) from 表名
//方差
SELECT VARIANCE(列名) from 表名

//标准差
SELECT STDEV(列名) from 表名

//变异系数
SELECT STDEV(列名)/AVG(列名) from 表名

4、R语言

4.1、说明
1）采用Pycharm 编辑器（加载R模块）。
2）加载路径：File -》 Settings -》Plugins -》 搜索R -》安装 R Language IntelliJ

4.2、实现

array <- c(1,2,3,4，4,5)

#中位数
mean(array)

#众数
mode <- unique(array)//去重
index <- tabulate(match(array,mode))//获取因素频率
mode[index == max(index)]//匹配所有频率最大值

#中位数
median(array)

#极差
max(array)-min(array)

#方差
var(array)

#标准差
sd(array)

#变异系数
sd(array)/mean(array)

5、Python

5.1、说明
采用Pycharm 编辑器，需要import 包名（建议采用线下安装方式，即本地下载包后pip，节省因网络波动导致的pip失败）。

numpy库说明：
NumPy(Numerical Python) 是 Python 语言的一个扩展程序库，支持大量的维度数组与矩阵运算，此外也针对数组运算提供大量的数学函数库。
教程指引：https://www.runoob.com/numpy/numpy-tutorial.html

Scipy是世界上著名的Python开源科学计算库，建立在Numpy之上。它增加的功能包括数值积分、最优化、统计和一些专用函数。 SciPy函数库在NumPy库的基础上增加了众多的数学、科学以及工程计算中常用的库函数。例如线性代数、常微分方程数值求解、信号处理、图像处理、稀疏矩阵等等。
5.2、实现

import numpy as np
from scipy import stats 

array = [1,2,3,4,4,5]

#平均数
print("平均数"+np.mean(array))

#众数
print("众数"+stats.mode(array)[0][0])

#中位数
print("中位数"+np.median(array))

#极差
print("极差"+(np.max(array)-np.min(array)))

#方差
print("方差"+np.var(array))

#变异系数
print("变异系数"+np.std(array)/np.mean(array))

#标准差
print("标准差"+np.std(array))