深入理解移动最小二乘法曲面拟合代码（MLS2D.m）

目录

 

摘要

下载代码

MLS2D 代码讲解

代码分析

MLS2D.m

MLS2Dshape.m

rectangle.m

代码改进

原代码不足之处

总结

---

• 摘要

       移动最小二乘法（Moving least squares，MLS）在我另外一篇博客有介绍。这里还是主要来说说MLS怎么做曲面拟合吧。代码在mathwork中和github上都有，我所用的是mathwork上的代码做了部分改进。本博客在现有代码基础上做了提速和增加随机采样点拟合方式的两方面改进，使得移动最小二乘法曲面代码适用性更为广泛。

1、提速。在i5 3450机上一幅98*144的图像以10等步长采样曲面拟合只需3s；

2、增加随机点曲面拟合方式。代码适用一堆离散点曲面拟合。

• 下载代码

       链接代码中分别有三种拟合计算方式：MLS1D、MLS2D和MLS3D，区别在于自变量个数不同，如自变量有一个，数据为{1,f(1);2,f(2)...}，那么用MLS1D；如果自变量有两个，如{(1,1),f(1,1);(1,2),f(1,2)...}，那么用MLS2D；有三个自变量，就用MLS3D。

• MLS2D 代码讲解

• 代码分析

       由于我的研究方向是图像处理，因此用MLS2D来做图像的曲面拟合，即给定一组整数坐标对及其对应的RGB颜色值，然后做曲面拟合。MLS2Dshape.m是具体实行代码。

首先感谢作者辛苦编写了该代码，原代码就不贴了，对照原代码我说下我们需要修改的地方。代码主体：

MLS2D.m

% SET UP NODAL COORDINATES     设置采样点
[xI,yI] = meshgrid(-2: 0.5 : 2);
nnodes = length(xI)*length(yI);

% SET UP COORDINATES OF EVALUATION POINTS  
[x,y] =meshgrid (-2 : 0.1: 2);
npoints = length(x)*length(y);
scale = 3;
% DETERMINE RADIUS OF SUPPORT OF EVERY NODE  支持半径
dmI = scale *0.5* ones(1, nnodes);

% Evaluate MLS shape function at all evaluation points x  
[PHI, DPHIx, DPHIy] = MLS2DShape(6, nnodes, xI,yI, npoints, x,y, dmI, 'GAUSS', 3.0 ); 

MLS2Dshape.m

......
%%计算每个节点在设置的半径内支撑域节点权值
    DmI = dmI;
	% DETERMINE WEIGHT FUNCTIONS AND THEIR DERIVATIVES AT EVERY NODE
	for i = 1 : nnodes
		[wI(i), dwdxI(i), dwdyI(i)] =rectangleWeight(type, para, 
        x(j),y(j),xI(i),yI(i),DmI(i),DmI(i));
       xII(1,i)=xI(i);
       yII(1,i)=yI(i);
    end
......
%%计算基函数
elseif (m == 6)
      p = [ones(1, nnodes); xII;yII; xII.*xII;xII.*yII;yII.*yII]; 
      pxy   = [1; x(j); y(j);x(j)*x(j);x(j)*y(j);y(j)*y(j)];
      dpdx  = [0; 1; 0;2*x(j);y(j);0];
      dpdy = [0;0;1;0;x(j);2*y(j)];
      
      B    = p .* [wI; wI; wI; wI; wI; wI];
      DBdx   = p .* [dwdxI; dwdxI;dwdxI;dwdxI; dwdxI;dwdxI];
      DBdy  = p .* [dwdyI; dwdyI;dwdyI;dwdyI; dwdyI;dwdyI];
end
......
%%构造A矩阵并求其逆
A   = zeros (m, m);
	DAdx  = zeros (m, m);
	DAdy= zeros (m, m);
	for i = 1 : nnodes
      pp = p(:,i) * p(:,i)';
      A   = A   + wI(i) * pp;
      DAdx  = DAdx  + dwdxI(i) * pp;
      DAdy = DAdy + dwdyI(i) * pp;
    end
   ARcond = rcond(A);  

%% A 矩阵病态，扩大支撑域半径，并重新从前开始计算A-1
 while ARcond<=9.999999e-015  %判断条件数
       DmI=1.1*DmI;
......

rectangle.m

%%高斯核函数，很简单，忽略dwdr计算
function [w,dwdr] = Gauss(beta,r)
if (r>1.0)
   w     = 0.0;
   dwdr  = 0.0;
  else
   b2 = beta*beta;
   r2 = r*r;
   eb2 = exp(-b2);

   w     = (exp(-b2*r2) - eb2) / (1.0 - eb2);
   dwdr  = -2*b2*r*exp(-b2*r2) / (1.0 - eb2);
   
end

运行该代码后，可能有两个问题：

1、rectangle函数不存在；

2、运行后什么也没有。

       作者已经单独上传了rectangle.m文件，运行后确实什么也没有，代码中也没有给显示代码。代码没有问题，我们给它稍微修改下，用来做图像的曲面拟合。代码有点长，修改了部分：

clc
clear all
I=imread('22result.jpg');
[row,col,chn]=size(I);
% I=I(1:col,:,:);
% 设置节点坐标
step=10;%步长
xII=1: step : row;
yII=1: step : col;
[xI,yI] = meshgrid(yII,xII);
nnodes = size(xI,1)*size(yI,2);
% 设置评估点的坐标
[x,y] = meshgrid(1: 1 : col,1: 1: row);

npoints = size(x,1)*size(y,2);
scale = 30;
% 确定每个节点的支持半径
dmI = scale *0.5* ones(1, nnodes);
tic
% 评估所有评估点x的MLS形状函数
[PHI, DPHIx, DPHIy] = MLS2DShape(6, nnodes, xI,yI, npoints, x,y, dmI, 'GAUSS', 3.0 ); 
toc
 
% 曲线拟合. y = peaks(x,y)
ZII  =I(xII,yII,:);    % 节点函数值 
% z  =x.*exp(-x.^2- y.^2);% 确切的解决方案
Zpoints=zeros(1,npoints);
xh=zeros(1,npoints);
yh=zeros(1,npoints);
II=I-I;
for i=1:npoints
% Zpoints(1,i)=z(i);
xh(1,i)=x(i);
yh(1,i)=y(i);
end
Znodes=zeros(1,nnodes);
for j=1:1
    ZI=ZII(:,:,j);
    for i=1:nnodes
        Znodes(1,i)=ZI(i);
    end                        %将二维数据转换为一维数据
    zh = PHI *Znodes';  % 逼近函数
    II(:,:,j)=reshape(zh,row,col);
end
ZI=double(ZI);
plot3( xI, yI, ZI,'k.','LineWidth',2);
hold on
surf(x,y,II(:,:,j));
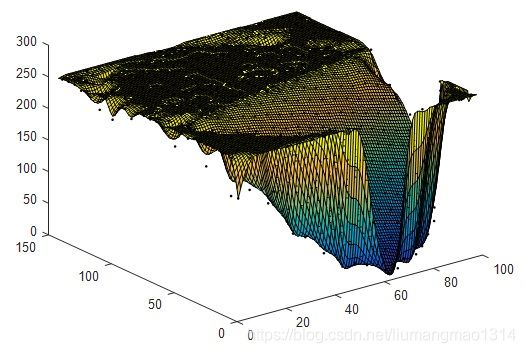
toc

MLS曲面拟合结果图，10等步长采样：

运行后发现一个小问题：运行时间很长。为此，我分析作者写的代码有些耗时之处：

1、MLS2Dshape.m中计算每个节点的支撑域权值w是用循环；

2、MLS2Dshape.m中当矩阵A是病态时，程序会重新计算基函数；

3、MLS2Dshape.m中用循环方法计算A。

我也就在此基础上进行了修改，可能还有其他优化的地方。

• 代码改进

1、计算支撑域权值w用矩阵计算；

2、基函数只计算一次；

3、矩阵A的计算替换循环。

4、当矩阵A病态时，增大它的扩大半径系数。

详细代码我上传到我的资源里了，大家可以去下载运行，在i5 3450机上一个98*144的图片以10个等步采样点拟合只需要3s。

• 原代码不足之处

       从原代码可以看到，代码作者只是做了等步长采样作为节点，但是有时候我们得到了一堆乱七八糟的散列点，或者图像曲面拟合时并不是方阵规则的区域，也想做曲面拟合，这时就需要对代码进行改进。限于篇幅，这里就不放了，在我资源里有，大家可以去下载，如果没有C币或积分，也可以发邮件直接问我要。不规则区域曲面拟合和随机采样点拟合类似，在不规则区域随机采样后即可拟合。代码下载链接：https://download.csdn.net/download/liumangmao1314/11132986

---

2019-05-21 更新

代码上传了百度网盘，有积分的还是给点积分吧。   仅供学习参考，禁止商业交易，请尊重作者~

提速代码 链接: https://pan.baidu.com/s/1GUmEK0AsZdnDcOT5ZaO50Q 提取码: b3d4 

随机采点 链接: https://pan.baidu.com/s/1G2c0keqs32RDMt72-CkcaA       提取码: k4ii 

---

运行结果图如下（200个随机采样点）：

• 总结

       本博客首先分析了移动最小二乘法曲面拟合的源代码MLS2D，并以源代码MLS2D的基础上进行了提速和拟合方式改进。改进后，速度上有较大的提升；同时，拟合方式增加一种随机采样点方式使得代码满足离散点拟合和不规则区域曲面拟合。

---------------------

热忱欢迎对图像矢量化有兴趣的同学一起沟通交流。