【面试题】全排列系列问题
题目一
解法一:回溯法(dfs实现)
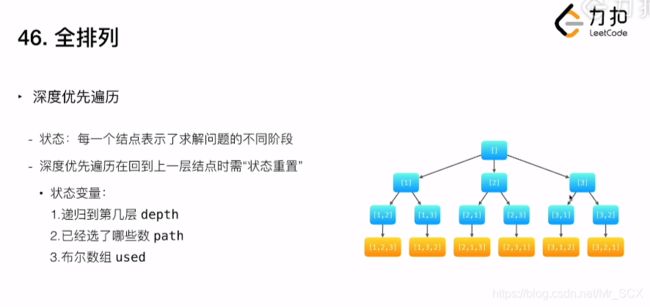
这个问题可以看作有 n 个排列成一行的空格,我们需要从左往右依此填入题目给定的 n 个数,每个数只能使用一次。那么很直接的可以想到一种穷举的算法,即从左往右每一个位置都依此尝试填入一个数,看能不能填完这 n 个空格,在程序中我们可以用「回溯法」来模拟这个过程。
定义递归函数 backtrack(index,path)表示当前从左往右填到第 index个位置上的排列结果为 path。整个递归函数分为两种情况:
- 若 index == n,说明我们已经填完了 n个位置(下标从 0开始,故 index = n时已经走到了数组末尾之外),即找到了一个可行解,将当前的排列结果 path 加入到 res中,递归结束。
- 如果 index < n,这时要考虑第 index个位置要填哪个数,根据题意我们肯定不能填已经填过的数字,所以很容易想到的一个解决思路是借助一个标记数组 visited[] 来标记已经填过的数字,这样一来,当我们在填第 index个位置时,遍历题目给定的 n个数,如果这个数字还没有被标记过,我们就尝试填入,并标记为已访问,然后继续尝试填下一个位置,即调用递归函数 backtrack(index+1,path)。当递归函数执行完回溯的时候,我们要撤销这个位置填的数及其标记,因为只有撤销了当前的选择,下一次搜索另一种排列结果时才有数可以选,这也正是回溯法的思想。
优化空间复杂度:标记数组需要申请额外的内存空间,那么有没有方法可以去掉这个标记数组?
我们可以借鉴排序算法中常常采用的原地置换方法,将含有 n个元素的数组 nums[]划分成两部分,左边是已经填过的数字,右边是待填的数字,我们在递归搜索的过程中只要动态维护这个数组即可。
具体来说,假设当前我们已经填到第 index个位置了,那么 nums[]中下标 0 ~ index-1 的位置上的元素均是已经填过的数,下标 index ~ n-1表示代填的数的集合,那么此时我们肯定是要从后半部分即 nums[index , n-1]中去寻找一个元素填入到当前 index的位置上,假设待填入的数字所在的下标为 i,那么填完之后我们将第 i个数和第 index个数交换,这样一来就能使得下一次在填第 index+1个位置时,nums[0 , index]均是已经填过的数字了,而nums[index+1 , n-1]为待填的数。然后,回溯的时候我们只要将这两个数交换回来即可撤销当前的选择。
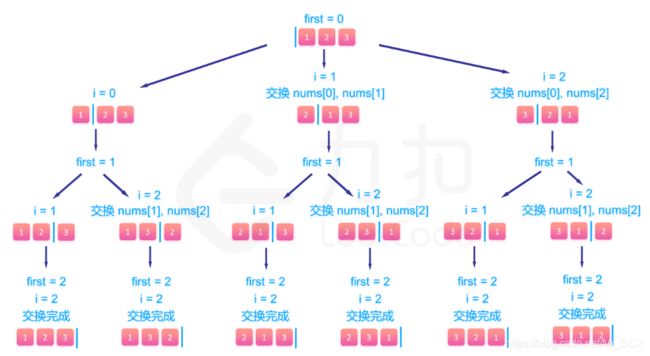
不过这个方法有个局限性,那就是这样生成的全排列并不是按字典序存储在答案数组中的,如果题目要求按字典序输出,那么请还是用标记数组或者其他方法。
Python
class Solution(object):
def permute(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
n = len(nums)
if n == 0: return []
self.res = []
self.backtrack(nums, index=0, path=[])
return self.res
def backtrack(self, nums, index, path):
# 满足结束条件,将当前搜索出的排列结果添加到 res中
# 由于 Python中list是可变对象,在递归中是全程只使用一份内存空间的,在dfs结束后,path就会退回到递归树的根结点,也即恢复一开始传入的空 []
# 因此,当满足条件时,应该添加的是当前 path的一份拷贝,直接 res.append(path)添加的只是 path的引用,会受到后续 path中元素变换的影响
if index == len(nums):
self.res.append(path[:]) # 使用切片[:]操作相当于浅拷贝,也可以显示调用copy.copy()函数
return
for i in range(index, len(nums)):
# 做选择
path.append(nums[i])
nums[index], nums[i] = nums[i], nums[index]
# 递归搜索
self.backtrack(nums, index+1, path)
# 撤销选择
path.pop()
nums[index], nums[i] = nums[i], nums[index]
另一种写法
class Solution(object):
def permute(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
n = len(nums)
res = []
if n == 0: return res
def backtrack(index):
if index == n:
res.append(nums[:])
return
for i in range(index, n):
nums[index], nums[i] = nums[i], nums[index]
backtrack(index+1)
nums[index], nums[i] = nums[i], nums[index]
backtrack(index=0)
return res
为了保持按字典序输出,采用标记数组的写法如下:
class Solution(object):
def permute(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
n = len(nums)
res = []
if n == 0: return res
visited = set() # 标记数组
def backtrack(depth, path): # depth:递归到了第几层 path:已经选择了哪些数字
if depth == n:
res.append(path[:])
return
for i in range(n):
if nums[i] in visited: continue # 判重
# 做选择
path.append(nums[i])
visited.add(nums[i]) # 访问过的标记为已使用
# 递归
backtrack(depth+1, path)
# 回溯,撤销操作
path.remove(nums[i])
visited.remove(nums[i])
backtrack(depth=0, path=[])
return res
Java
class Solution {
public List<List<Integer>> res = new LinkedList<>();
// 主函数:输入一组不重复的数字,返回它们的全排列
public List<List<Integer>> permute(int[] nums) {
LinkedList<Integer> track = new LinkedList<>();
backtrack(nums, track);
return res;
}
/**
* track: 记录路径
* 选择列表:nums中还未加入到 track中的那些元素
* 结束条件:nums中的元素全部出现添加到了 track中
*/
public void backtrack(int[] nums, LinkedList<Integer> track){
if(track.size() == nums.length){
// 结束条件
res.add(new LinkedList(track));
return;
}
for(int i=0; i<nums.length; i++){
if(track.contains(nums[i])) continue; // 排除不合法的选择
track.add(nums[i]); // 做选择
backtrack(nums, track); // 递归进入下一层决策
track.removeLast(); // 撤销选择
}
}
}
参考
https://leetcode-cn.com/problems/permutations/solution/hui-su-suan-fa-python-dai-ma-java-dai-ma-by-liweiw/
题目二

这道题在上一题的基础上增加了“序列中的元素可重复”这一条件,但要求返回的结果又不能有重复元素。
一个比较容易想到的办法是在结果集中去重。但是问题又来了,这些结果集的元素是一个又一个列表,对列表去重不像用哈希表对基本元素去重那样容易。如果硬要比较两个列表是否一样,一个很显然的办法是分别排序后,然后从头遍历列表逐个比对。(当然,在 Python中就可以很简洁地判定两个 list是否一样= =,但其实底层应该也是先排序再逐个元素对比吧)
利用 Python实现的代码如下(非常简单,只是在原来的基础上加多一个结果的判重):
class Solution(object):
def permuteUnique(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
if len(nums) == 0: return []
res = []
def backtrack(index):
if index == len(nums) and nums[:] not in res:
res.append(nums[:])
for i in range(index, len(nums)):
nums[index], nums[i] = nums[i], nums[index]
backtrack(index+1)
nums[index], nums[i] = nums[i], nums[index]
backtrack(index=0)
return res
解决思路:既然要排序,我们可以在搜索之前就对候选数组进行排序,一旦发现在递归树的搜索过程中,这一分支搜索下去可能搜索到重复的元素就停止搜索,也就是在一定会产生重复结果集的地方进行剪枝,这样结果集中不会包含重复元素。
class Solution(object):
def permuteUnique(self, nums):
"""
:type nums: List[int]
:rtype: List[List[int]]
"""
if len(nums) == 0: return []
used = [False]*len(nums) # 标记数组
nums.sort() # 搜索前先排序,方便后续剪枝
res = []
def backtrack(depth, path):
if depth == len(nums):
res.append(path[:])
return
for i in range(len(nums)):
if used[i] == True: # 判重
continue
if i > 0 and nums[i] == nums[i-1] and used[i-1] == False: # 当前的数和上次一样,若used[i-1] == False说明上一个相同的数刚刚被撤销选择,那么下面的搜索中就还会使用到,这就会产生重复了,故应该剪枝。
continue
# 做选择
used[i] = True
path.append(nums[i])
# 递归
backtrack(depth+1, path)
# 撤销选择
path.pop()
used[i] = False
backtrack(depth=0, path=[])
return res
其实,if 条件语句中 used[i-1] == False 改为判断 used[i-1] == True 也是可以的,区别在于结果保留的是相同元素的顺序索引还是倒序索引,很明显,顺序索引(即使用 used[i-1] == False 作为剪枝判定条件)得到的递归树剪枝更加彻底,思路也相对较自然。具体分析可参考这篇文章。
