【软件分析学习笔记】3：静态程序分析(Static Program Analysis)介绍

最近的南大软件分析课，讲的就完全是静态分析的内容，目前先跟着这个课学习软件分析的内容，北大熊老师的课光看课件太难懂了。

1 PL和静态分析的背景

之前吴老师也提到，做形式化也是在做PL(Programing Language)。这里李老师将PL分成三部分：

1. 理论部分：语言设计、类型系统、形式语义和程序逻辑等。即在理论上构建出一个语言。
2. 环境部分：编译、运行时系统等。即相应的支撑语言运行的一套系统。
3. 应用部分：程序分析、程序验证、程序合成等。在语言层面谈到程序分析，实际上指的就是静态程序分析。

从软工的角度来看很多人做的程序分析是动态分析，但在PL领域的程序分析是静态分析。

语言千变万化，但是语言的核心部分没有太大变化，可以分为三类：

1. 命令式语言：如Java/C/C++，将程序逻辑拆解成一条条命令按序运行。
2. 函数式语言：如Haskell，JavaScript和Python也支持函数式编程，将逻辑用函数包装起来。
3. 逻辑式语言：也即声明式语言，通过逻辑与或非声明得到结果。（这里没懂）

语言的核心没有什么变化，但是语用环境变了，因为需求变得越来越多，用程序语言写的程序越来越大。如何在更大规模、更复杂的程序里保证其可靠性(reliability)和安全性(security)变成了一个重要的问题，所以PL的应用部分变得越来越重要。

2 为什么需要静态分析

静态分析也就是在程序运行之前，在编译时期完成所有的分析过程，"静态"即不用去运行程序就能进行分析。

2.1 检测reliability相关的问题

例如，要避免空指针引用(null pointer dereference)，如Java运行时的NullPointerException。又如，要避免内存泄漏(memory leak)，如C中malloc的空间一直没有free掉。

2.2 检测security相关的问题

例如，要避免私有信息泄漏(private information leak)，如在安卓某个应用中输入的账号密码不应被其它应用劫持。又如，要避免注入攻击(injection attack)，如SQL注入可以恶意操作服务器数据库。

2.3 编译优化(compiler optimization)

编译优化是编译器后端的部分，大部分的编译优化（除了JIT那种在线的）用的都是静态分析的技术。例如，死代码消除(dead code elimination)，即将永远不可能执行到的代码删除。又如，代码移动(code motion)，如将循环内部和循环无关的重复计算提到循环的外面。

2.4 程序理解(program understanding)

如很多IDE中能追踪函数调用的层级关系(IDE call hierarchy)。又如类型提示(type indication)，对动态类型的语言这个尤为重要。

3 莱斯定理

3.1 简述

静态分析，就是在运行程序之前就要了解程序的所有行为，并能够知道一些性质在这个程序中能否得到满足。除了要能回答2中的那些问题，还有比如：

• 程序运行时的类型转换(cast)是安全的吗？
• 变量$v_1$和$v_2$在运行时可能指向同一块内存吗？
• 程序中的断言(assert)在运行时会不会fail？

根据莱斯定理，没法给出准确的Yes/No的回答。这里李老师对莱斯定理的解释是，对于r.e. language，它的non-trivial的性质都是不可判断的。

这里r.e. language是递归可枚举(recursively enumerable)的语言，也就是图灵机可识别的语言。

关于非平凡属性的具体解释还是见笔记1中熊老师课件上的解释。

3.2 perfect = sound & complete

总之，莱斯定理指出不存在perfect static analysis。这里perfect指的是既sound又complete的。

sound就是包含了事实的命题，如对于【程序中有10个空指针引用】而言，【程序中有空指针引用】就是它之上的一个sound的命题。

complete是被事实所包含的命题，如但对于【程序中有10个空指针引用】而言，【在程序中找到了5个空指针引用】甚至【程序中没有找到空指针引用】都是其下的complete的命题。

不存在perfect的静态分析，也就是不存在既sound又complete从而能将truth准确的圈在这个范围里的方法。

3.3 useful = 妥协sound | 妥协complete

但是，存在useful static analysis，这里的useful是在perfect的两个组成——sound和complete中妥协一方得到的。即如下两种情况中的一个：

1. compromise soundness(false negatives)，即会产生漏报，如10个空引用只找出其中5个。
2. compromise completeness(false positives)，即会产生误报，如除了10个空引用之外，还找出了不是空引用的部分误认为是。

在几乎所有的静态分析中都是去妥协complete，即便有误报也不希望产生漏报，不去妥协sound。因为sound对于编译优化或程序验证这类领域是非常重要的，如果妥协了sound可能会给出错误的结论。

例如，下图中要检测强制转换是不是安全的：

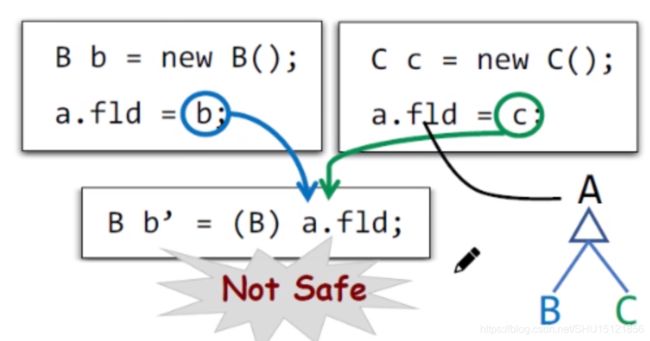
如果妥协了sound，会导致分析不全面，如果只分析了左边的路径，那么会发现这个类型转换是安全的，但实际运行时可能还有右边的路径，却没有被分析到，这样妥协sound就得出了错误的论断。

4 静态分析的精度和代价

例如对程序：

if(input)
	x = 1
else
	x = 0

分析变量x在运行后的值，如有两种静态分析，分别给出了如下的结果：

1. 当input为真x=1，否则x=0
2. x=1或者x=0

这两种静态分析结果都是正确的，因为都保证了soundness。第一种更加精确，花费的代价也更大，因为需要保存和分析input的状态。第二种不那么精确，但是代价却比较低。静态分析就是在保证soundness的同时，在精度和代价之间折衷，这样才能得到一个真正有用的静态分析。这里的代价越高，分析程序所需要的时间也会越长，试想一个编译优化程序如果要运行5个小时，很大程度上是无法接受的。

5 抽象和过近似

这是构筑静态分析最基本的思路。

5.1 抽象(abstraction)

这里老师举的也是符号分析的例子，要判定的是每个变量运算后的符号，这里的"抽象"就是将变量的具体值抽象到了$+$、$-$、$0$、$\top$（未知）、$\perp$（未定义）：

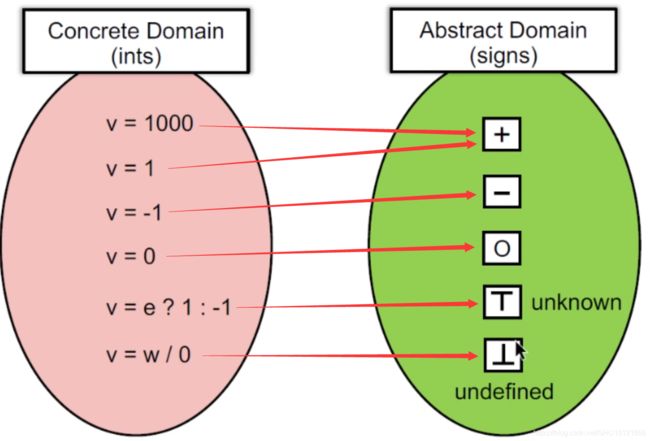
5.2 过近似——转换函数

要进行过近似(over-approximation)，就要去定义一套规则，最基本的是转换函数(transfer functions)，即针对程序中的每一条语句，对抽象域上的结果提供转换规则。

转换规则是根据所分析的问题，以及程序中每条语句的语义，来综合设计的。例如，符号分析的转换规则：

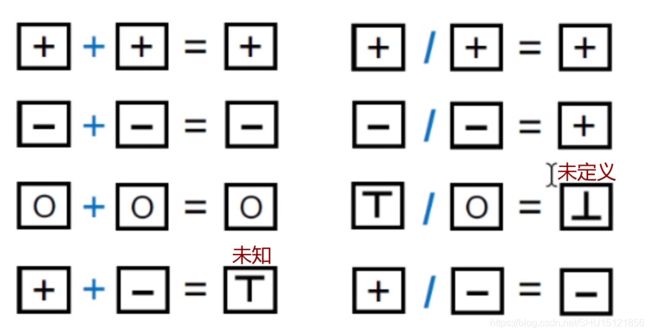
注意这里标出来的两条规则，即是为了保证静态分析是soundness的，必须要给出一个囊括truth的结果。

5.3 计算过程

利用5.2和5.1，就可以对程序进行静态的符号分析：

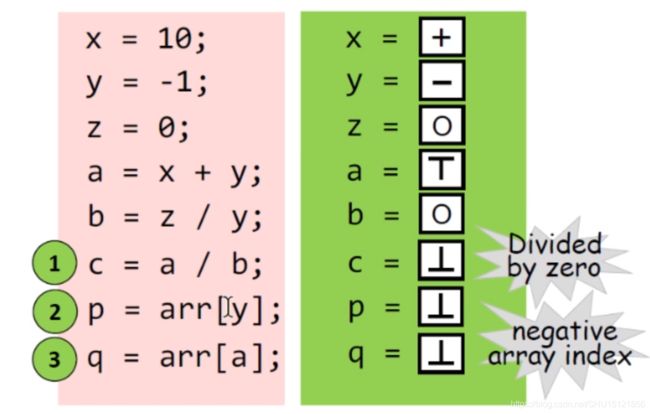
注意倒数两行，只要数组下标有取[$-$]的可能性（这里$y$是[$-$]而$a$是[$\top$]），那么结果就应该是[$\perp$]表示未定义，遵循即使误报也不应漏报的原则（实际运行下来可知，最后一行是误报）。

5.4 过近似——控制流

上面的例子是只有顺序语句的例子，当存在条件控制的语句时，就会在控制流(control flows) 上出现分支和汇聚的点，控制流图汇聚的地方要计算抽象域上的汇聚规则。例如，一个简单的条件判断会产生分支，并在条件判断语句结束后汇合：

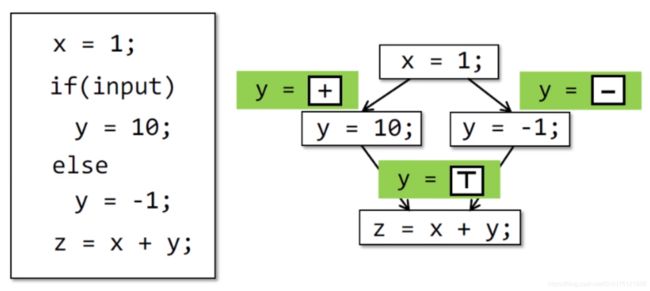
转换函数和控制流共同为整个程序完成over-approximation。