【Study Notes】Mathematics for Machine Learning: Linear Algebra (Week 2)
Introduction
This is a study note of the course Mathematics for Machine Learning: Linear Algebra on the coursera. In week 2 section, we will look at vector’s modulus, and look at a way to combine vectors together to get the dot product, which can take us on to find the scalar and vector projections. In addition, basis vector and vector space will be defined in this section, and we will learn how to prove linear independence and linear combination.
Modulus
Modulus is length of a vector, so if a vector is given r = a i ^ + b j ^ = [ a b ] r=a\hat i+b\hat j = \begin{bmatrix} a\\b\\ \end{bmatrix} r=ai^+bj^=[ab], the modulus of vector r r r is equal to ∣ r ∣ = a 2 + b 2 |r| = \sqrt{a^2+b^2} ∣r∣=a2+b2 . In addition, we also use dot product to get the modulus of a vector, i.e. we can get the modulus of a vector by the vector dotted by itself, ∣ r ∣ 2 = r ⋅ r = [ a b ] ⋅ [ a b ] = a 2 + b 2 |r|^2=r\cdot r= \begin{bmatrix} a\\b\\ \end{bmatrix}\cdot \begin{bmatrix} a\\b\\ \end{bmatrix}=a^2+b^2 ∣r∣2=r⋅r=[ab]⋅[ab]=a2+b2 .
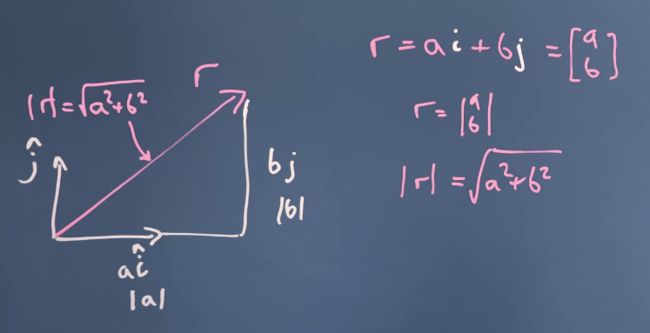
Dot Product
The dot product is a scalar number given by multiplying the components of the vector in turn, and adding those up. e.g. given two vector r = [ r 1 r 2 ⋮ r n ] r = \begin{bmatrix}r_1\\r_2\\ \vdots \\r_n\\ \end{bmatrix} r=⎣⎢⎢⎢⎡r1r2⋮rn⎦⎥⎥⎥⎤ and s = [ s 1 s 2 ⋮ s n ] s = \begin{bmatrix}s_1\\s_2\\\vdots\\s_n\\ \end{bmatrix} s=⎣⎢⎢⎢⎡s1s2⋮sn⎦⎥⎥⎥⎤, we can find the dot product is r ⋅ s = r 1 s 1 + r 2 s 2 + ⋯ + r n s n r\cdot s =r_1s_1+r_2s_2+\cdots+r_ns_n r⋅s=r1s1+r2s2+⋯+rnsn .
- commutative: r ⋅ s r\cdot s r⋅s is equal to s ⋅ r s\cdot r s⋅r .
- distributive: r ⋅ ( s + t ) r\cdot (s+t) r⋅(s+t) is equal to r ⋅ s + r ⋅ t r\cdot s+r\cdot t r⋅s+r⋅t .
- associative: r ⋅ ( a s ) r\cdot(as) r⋅(as) is equal to a ( r ⋅ s ) a(r\cdot s) a(r⋅s), where a a a is a scalar.
Interestingly, if we take the dot product of a vector with itself, we can get the square of its size of its modulus. i.e. ∣ r ∣ 2 = r ⋅ r = [ a b ] ⋅ [ a b ] = a 2 + b 2 |r|^2=r\cdot r= \begin{bmatrix} a\\b\\ \end{bmatrix}\cdot \begin{bmatrix} a\\b\\ \end{bmatrix}=a^2+b^2 ∣r∣2=r⋅r=[ab]⋅[ab]=a2+b2.
Cosine & Dot Product
Let’s start from a right triangle. For a right triangle, it have 3 egdes, respectively called legs if the side adjacent to the right angle, and called hypotenuse if the side oppsite the right angle.
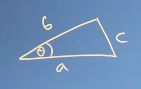
According consine rule, we get a equation.
c 2 = a 2 + b 2 − 2 a b cos θ c^2=a^2+b^2-2ab\cos\theta c2=a2+b2−2abcosθ
Then we define a vector s s s and a vector r r r as the following figure.

∣ r − s ∣ 2 = ∣ r ∣ 2 + ∣ s ∣ 2 − 2 ∣ r ∣ ∣ s ∣ cos θ (1) |r-s|^2=|r|^2+|s|^2-2|r||s|\cos\theta \tag{1} ∣r−s∣2=∣r∣2+∣s∣2−2∣r∣∣s∣cosθ(1)
Let’s make dot product of r − s r-s r−s with itself.
( r − s ) ⋅ ( r − s ) = r ⋅ r − s ⋅ r − s ⋅ r + s ⋅ s = ∣ r ∣ 2 − 2 s ⋅ r + ∣ s ∣ 2 (2) \begin{aligned} (r-s)\cdot(r-s)&=r\cdot r-s\cdot r-s\cdot r+s\cdot s\\ &=|r|^2-2s\cdot r + |s|^2\tag{2}\\ \end{aligned} (r−s)⋅(r−s)=r⋅r−s⋅r−s⋅r+s⋅s=∣r∣2−2s⋅r+∣s∣2(2)
Then, we do that comparison between ( 1 ) (1) (1) and ( 2 ) (2) (2).
r ⋅ s = ∣ r ∣ ∣ s ∣ cos θ r\cdot s=|r||s|\cos\theta r⋅s=∣r∣∣s∣cosθ
- r ⋅ s = ∣ r ∣ ∣ s ∣ cos θ r\cdot s=|r||s|\cos\theta r⋅s=∣r∣∣s∣cosθ
- θ = 9 0 ∘ \theta=90^\circ θ=90∘, r ⋅ s = ∣ r ∣ ∣ s ∣ cos θ = 0 r\cdot s=|r||s|\cos\theta=0 r⋅s=∣r∣∣s∣cosθ=0.
- θ = 0 ∘ \theta=0^\circ θ=0∘, r ⋅ s = ∣ r ∣ ∣ s ∣ cos θ = ∣ r ∣ ∣ s ∣ r\cdot s=|r||s|\cos\theta=|r||s| r⋅s=∣r∣∣s∣cosθ=∣r∣∣s∣
- θ = 18 0 ∘ \theta=180^\circ θ=180∘, r ⋅ s = ∣ r ∣ ∣ s ∣ cos θ = − ∣ r ∣ ∣ s ∣ r\cdot s=|r||s|\cos\theta=-|r||s| r⋅s=∣r∣∣s∣cosθ=−∣r∣∣s∣
Vector Projection
Given two vector as following figure, we can make the projection of the vector s s s onto the vector r r r.

Obviously, we can get cos θ = adj hyp = adj ∣ s ∣ \cos\theta={\text{adj}\over{\text{hyp}}}={ {\text{adj}}\over{|s|}} cosθ=hypadj=∣s∣adj in the right triangle.
In addition, we use dot product to get a equation r ⋅ s = ∣ r ∣ ∣ s ∣ cos θ r\cdot s = |r||s|\cos\theta r⋅s=∣r∣∣s∣cosθ.
So, ∣ s ∣ cos θ = r ⋅ s ∣ r ∣ |s|\cos\theta={ {r\cdot s}\over{|r|}} ∣s∣cosθ=∣r∣r⋅s is used to take the scalar projection of vetor s s s onto the vector r r r.
We also can get the vector projection by using r ⋅ s ∣ r ∣ ∣ r ∣ × r = r ⋅ s r ⋅ r × r { {r\cdot s} \over {|r||r|}}\times r={ {r\cdot s} \over {r\cdot r}}\times r ∣r∣∣r∣r⋅s×r=r⋅rr⋅s×r.
- scalar projection: ∣ s ∣ cos θ = r ⋅ s ∣ r ∣ |s|\cos\theta={ {r\cdot s}\over{|r|}} ∣s∣cosθ=∣r∣r⋅s
- vector projection: r ⋅ s ∣ r ∣ ∣ r ∣ × r = r ⋅ s r ⋅ r × r { {r\cdot s} \over {|r||r|}}\times r={ {r\cdot s} \over {r\cdot r}}\times r ∣r∣∣r∣r⋅s×r=r⋅rr⋅s×r
Linear Dependence & Independence
Linear Dependence
Vectors are linearly dependent if it is possible to write one vector as a linear combination of the others. For example, the vectors a a a, b b b and c c c are linearly dependent if a = q 1 b + q 2 c a=q_1b+q_2c a=q1b+q2c where q 1 q_1 q1 and q 2 q_2 q2 are scalars.
Linear Independence
We say that two vectors are linearly independent if they are not linearly dependent, that is, we cannot write one of the vectors as a linear combination of the others.