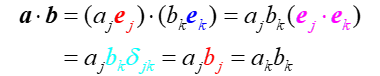张量基础学习（一 概念，求和指标，符号）
欢迎大家来到我的这一个新专栏，本专栏我们将一起学习并探讨一些张量方面的知识，同样，需要一定的线性代数的基础知识铺垫，但肯定是没有量子计算那么深入和复杂，有需要的小伙伴可以点点关注，您的鼓励是我前进的最大动力！
Tensor
- 一. 张量基本概念
- 二. 爱因斯坦求和约定
- 三. 符号 δ i j \delta_{ij} δij 与 e r s t e_{rst} erst
-
- (1) δ i j \delta_{ij} δij 符号
- (2) e r s t e_{rst} erst 符号
一. 张量基本概念
张量（tensor）理论是数学的一个分支学科，在力学中有重要应用。张量这一术语起源于力学，它最初是用来表示弹性介质中各点应力状态的，后来张量理论发展成为力学和物理学的一个有力的数学工具。张量之所以重要，在于它可以满足一切物理定律必须与坐标系的选择无关的特性。张量概念是矢量概念的推广，矢量是一阶张量。张量是一个可用来表示在一些矢量、标量和其他张量之间的线性关系的多线性函数!
我们在后面的机器学习 ，深度学习，还有最重要的量子计算与量子机器学习中，张量分解与张量分析都发挥着举足轻重的作用，所以，我们希望能尽量将它学好！
从定义开始，“张量” 在不同的场景下有不同的定义：
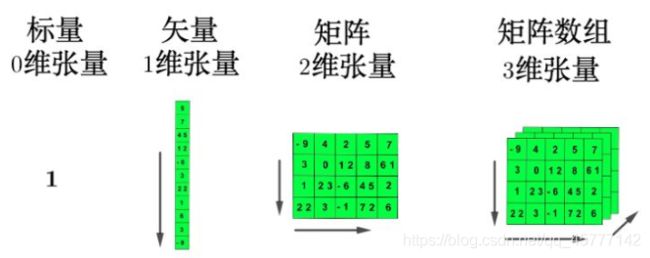
- 张量是某种多维数组，这个非常好理解。
- 张量是某种几何对象，不会因坐标系的改变而发生改变
- 张量是向量和余向量 通过张量积组合而成的！
- 张量是多重线性映射，即：
我们在量子计算二这一篇博客中就为大家简单的介绍过张量的其中一种定义，同时也介绍了张量积的运算法则和一些性质，具体的大家可以去我的量子计算专栏中寻找，在这里，我们还是从头开始继续了解一下！
张量是向量和矩阵的自然推广，向量可称为一阶张量，矩阵可称为二阶张量，将矩阵堆叠形成“立方体”，这种数据结构则称为三阶张量。一张灰度图像在计算机中由矩阵表示，是二阶张量。一张RGB三通道的彩色图像在计算机中则保存为三阶张量。当然，三阶张量也可以堆叠形成更高阶的张量。
还有一个视频可以帮助你更加深入理解！
张量理解
我们用多维数组来进一步理解：
其中，阶（order/ways/modes/rank）：就是张成所属张量空间的向量空间的个数，秩 就可以理解成[ 的个数（深度），例如
二. 爱因斯坦求和约定
这个名字我们有的同学可能第一次听，但都是我们经常用的，也是非常的简单！
For example:
S = a 1 x + a 1 x + ⋯ + a n x n S =a_{1}x_{}+a_{1}x_{}+\cdots+a_{n}x_{n} S=a1x+a1x+⋯+anxn
用求和符号来表示就是：
S = ∑ i = 1 n a i x i = ∑ j = 1 n a j x j S=\sum_{i=1}^{n} a_{i} x_{i}=\sum_{j=1}^{n} a_{j} x_{j} S=i=1∑naixi=j=1∑najxj
我们约定 ： S = a i x i = a j x j S = a_{i}x_{i} = a_{j}x_{j} S=aixi=ajxj，求和指标与所用字母无关，且指标只能重复一次！
多个变量同时出现的话，可以进行双重求和：
∑ i = 1 3 ∑ j = 1 3 A i j x i y j = A 11 x 1 y 1 + A 12 x 1 y 2 + A 13 x 1 y 3 + A 21 x 2 y 1 + A 22 x 2 y 2 + A 23 x 2 y 3 + A 31 x 3 y 1 + A 32 x 3 y 2 + A 33 x 3 y 3 \begin{aligned} \sum_{i=1}^{3} \sum_{j=1}^{3} A_{i j} x_{i} y_{j}=& A_{11} x_{1} y_{1}+A_{12} x_{1} y_{2}+A_{13} x_{1} y_{3}+\\ & A_{21} x_{2} y_{1}+A_{22} x_{2} y_{2}+A_{23} x_{2} y_{3}+\\ & A_{31} x_{3} y_{1}+A_{32} x_{3} y_{2}+A_{33} x_{3} y_{3} \end{aligned} i=1∑3j=1∑3Aijxiyj=A11x1y1+A12x1y2+A13x1y3+A21x2y1+A22x2y2+A23x2y3+A31x3y1+A32x3y2+A33x3y3
这里不能看出有就像，再填上一个Z，就会有27项了： A i j k x i y j z k A_{i j k} x_{i} y_{j} z_{k} Aijkxiyjzk
指标（下标）这么多，我们来给它们分个类，先看个例子：
A 11 x 1 + A 12 x 2 + A 13 x 3 = b 1 A 21 x 1 + A 22 x 2 + A 23 x 3 = b 2 A 31 x 1 + A 32 x 2 + A 33 x 3 = b 3 \begin{array}{l} A_{11} x_{1}+A_{12} x_{2}+A_{13} x_{3}=b_{1} \\ A_{21} x_{1}+A_{22} x_{2}+A_{23} x_{3}=b_{2} \\ A_{31} x_{1}+A_{32} x_{2}+A_{33} x_{3}=b_{3} \end{array} A11x1+A12x2+A13x3=b1A21x1+A22x2+A23x3=b2A31x1+A32x2+A33x3=b3
注意事项：
- 在表达式或方程中自由指标可以出现多次，但不得在同项内出现两次，若在同项 内出现两次则是哑指标！
- 由于哑标 i i i 仅要求遍历求和，故可以成对地任意交换，只要其在同项内仅出现2次，且取值范围和 i i i 相同即可(这里是矢量点积)！
a ⋅ b = a j b j = a m b m \boldsymbol{a\cdot b} = a_{j}b_{j}= a_{m}b_{m} a⋅b=ajbj=ambm - 我们通长约定：如果在表明取值范围，则拉丁指标 i , j , k i,j,k i,j,k 等 表示三维指标，取值1，2 ，3；而希腊字母指标 α ， β ， γ \alpha ，\beta， \gamma α，β，γ等均为 二维指标，取值1，2！
- 在后面使用张量的时候，注意 同时取值的自由指标必须同名，独立取值的自由指标应防止重名。
- 自由指标必须整体换名，即把方程或表达式中出现的同名自由指标全部改成同一个新名字
总结一下：
通过哑指标可把许多项缩写成一项，通过自由指标又把许多方程缩写成一个方程。
一般说，在一个用指标符号写出的方程中，若有 k 个独立的自由指标，其取值范围是1～n，则这个方程代表了 n k n^{k} nk个分量方程。在方程的某项中若同时出现 m 对取值范围为1～n 的哑指标，则此项含相互迭加的 n m n^{m} nm 个项!
还需要知道一点的就是，指标符号也适用于微分和导数表达式！
这大概就是我们目前需要掌握的爱因斯坦求和约定的相关部分 ！
三. 符号 δ i j \delta_{ij} δij 与 e r s t e_{rst} erst
(1) δ i j \delta_{ij} δij 符号
在笛卡尔坐标系中，下图中三个相互正交的单位基矢量 构成一个正交标准化基
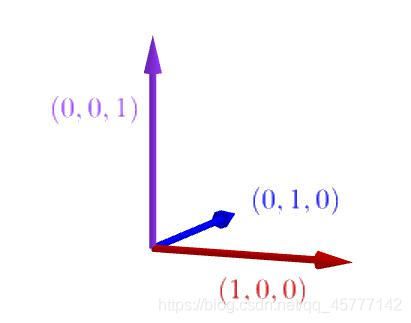我们先定义 δ i j \delta_{ij} δij：
δ i j = e i ⋅ e j = { e i ⋅ e j = 1 ( i = j ) e i ⋅ e j = 0 ( i ≠ j ) \delta_{ij} = e_{i}\cdot e_{j}=\left\{\begin{array}{l} e_{i} \cdot e_{j}=1(i=j) \\ e_{i} \cdot e_{j}=0(i \neq j) \end{array}\right. δij=ei⋅ej={ ei⋅ej=1(i=j)ei⋅ej=0(i=j)
这个定义是非常好理解的，在线代学习中内积的那一部分和这个相类似，只是但是似乎并没有介绍这个符号！下面介绍一下它的几个性质特点：
- 对称性，有定义可知 δ i j = δ j i \delta_{ij}=\delta_{ji} δij=δji .
- δ i j \delta_{ij} δij 的分量集合对应的矩阵恰好是单位矩阵：
[ δ 11 δ 12 δ 13 δ 21 δ 22 δ 23 δ 31 δ 32 δ 33 ] = [ 1 0 0 0 1 0 0 0 1 ] \left[\begin{array}{lll} \delta_{11} & \delta_{12} & \delta_{13} \\ \delta_{21} & \delta_{22} & \delta_{23} \\ \delta_{31} & \delta_{32} & \delta_{33} \end{array}\right]=\left[\begin{array}{lll} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] ⎣⎡δ11δ21δ31δ12δ22δ32δ13δ23δ33⎦⎤=⎣⎡100010001⎦⎤ - 换标作用：如果符号 δ i j \delta_{ij} δij 的两个指标中，有一个和同项中其它因子的指标相重，则可以把该因子的那个重指标换成 δ i j \delta_{ij} δij 的另一个指标，而 δ \delta δ 自动消失。
δ i j a j k = a i k ； δ i j a i k = a j k δ i j a k j = a k i ； δ i j a k i = a k j δ i j δ j k = δ i k ； δ i j δ j k δ k l = δ i l \begin{array}{l} \delta_{i j} a_{j k}=a_{i k} ；\delta_{i j} a_{i k}=a_{j k} \\ \delta_{i j} a_{k j}=a_{k i} ；\delta_{i j} a_{k i}=a_{k j} \\ \delta_{i j} \delta_{j k}=\delta_{i k} ； \delta_{i j} \delta_{j k} \delta_{k l}=\delta_{i l} \end{array} δijajk=aik；δijaik=ajkδijakj=aki；δijaki=akjδijδjk=δik；δijδjkδkl=δil
(2) e r s t e_{rst} erst 符号
e r s t e_{rst} erst 符号为：排列符号或者是置换符号，Eddington。
在笛卡尔坐标系中，我们定义如下：
e r s t = { 1 当r, s , 为正序排列时 − 1 当 r , s , t 为逆序排列时 0 当r , s , t 中两个指标值相同时 e_{r s t}=\left\{\begin{array}{ll}1 & \text { 当r, } s, \text { 为正序排列时 } \\ -1 & 当 r, s, t \text { 为逆序排列时 } \\ 0 & \text { 当r }, s, t \text { 中两个指标值相同时 }\end{array}\right. erst=⎩⎨⎧1−10 当r, s, 为正序排列时 当r,s,t 为逆序排列时 当r ,s,t 中两个指标值相同时
由于 r , s , t r, s, t r,s,t 只能在1，2，3中选取，所以上述公式还可写成
e r s t = 1 2 ( r − s ) ( s − t ) ( t − r ) e_{rst} = \frac{1}{2}(r-s)(s-t)(t-r) erst=21(r−s)(s−t)(t−r)
第三种取0的情况比较好理解，那么我们什么时候取-1，什么时候取1呢？
(1,2,3)及其轮流换位得到的(2,3,1)和(3,1,2)称为正序排列。
(3,2,1)及其轮流换位得到的(2,1,3)和(1,3,2)称为逆序排列
这里依然有一个视频，帮助大家理解：
排列符号或置换符号简单演示
来接着看看这个 e r s t e_{rst} erst 符号的一些基本性质:
- 根据排列组合原理，每个位置有三种可能，所以共有27个元素，其中有三种元素为1，三种元素为-1，其余元素都是0！
- 反对称性：对于其中任何两个指标，有
e r s t = − e s t r = − e t r s = − e t s r e_{rst}= -e_{str} = -e_{trs} = -e_{tsr} erst=−estr=−etrs=−etsr - 当三个指标轮流换位时（相当于指标连续兑换两次）， e r s t e_{rst} erst 的值不变 ： e r s t = e s t r = e t r s e_{rst} =e_{str} = e_{trs} erst=estr=etrs
综上，矢量的点积可以写成为：
好，张量学习的第一部分就到这里了，下期再见~~