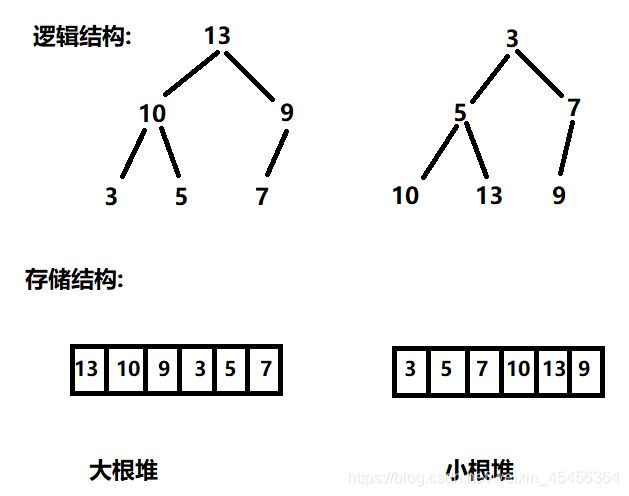
优先级队列(堆),以及TopK问题

• 逻辑意义上是一棵完全二叉树
• 物理意义上存储在数组中
  

向下调整

大根堆为例

public static void adjustDown(int[] elem,int root, int len) {
     
        int parent = root;
        int child = 2 * parent + 1;
        while (child < len) {
     
//判断是否有右孩子,且谁最大
            if (child + 1 < len && elem[child] < elem[child + 1]) {
     
                child = child + 1;
            }
            if (elem[child] > elem[parent]) {
     //child肯定是左右孩子最大值的下标
                int t = elem[child];
                elem[child] = elem[parent];
                elem[parent] = t;
                parent = child;
                child = 2 * parent + 1;
            }else{
     
                break;
            }
        }
    }

建堆

public static void createHeap(int[] array){
     
        for (int i = (array.length-1-1)/2; i >= 0 ; i--) {
     
            adjustDown(array,i,array.length);
        }
}

优先级队列PriorityQueue

  //向上调整
    public void adjustUp(int child) {
     
        int parent = (child - 1) / 2;
        while (child > 0) {
     
            if (this.elem[child] > this.elem[parent]) {
     
                int tmp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = tmp;
                child = parent;
                parent = (child - 1) / 2;
            } else {
     
                break;
            }
        }
    }

    //判断是否满了
    public boolean isFull() {
     
        return this.usedSize == this.elem.length;
    }

    //入堆
    public void pushHeap(int val) {
     
        if (isFull()) {
     //扩容
            this.elem = Arrays.copyOf(this.elem, this.elem.length * 2);
        }
        this.elem[this.usedSize] = val;
        this.usedSize++;
        adjustUp(usedSize - 1);
    }

    //判断是否为空
    public boolean isEmpty() {
     
        return usedSize == 0;
    }

    //出堆
    public void popHeap() {
     
        if (isEmpty()) {
     
            return;
        }
        int tmp = this.elem[0];
        this.elem[0] = this.elem[this.usedSize - 1];
        this.elem[this.usedSize - 1] = tmp;
        this.usedSize--;
        adjustDown(0, this.usedSize);
    }

    //获取元素
    public int getPop() {
     
        if (isEmpty()) {
     
            return -1;
        }
        return this.elem[0];
    }

    //打印
    public void display() {
     
        for (int i = 0; i < this.usedSize; i++) {
     
            System.out.println(this.elem[i] + "");
        }
        System.out.println();
    }

TopK问题

用堆来解决
如果是求当前最大的K个元素;就应该用小根堆,反之用大根堆
具体思路如下:

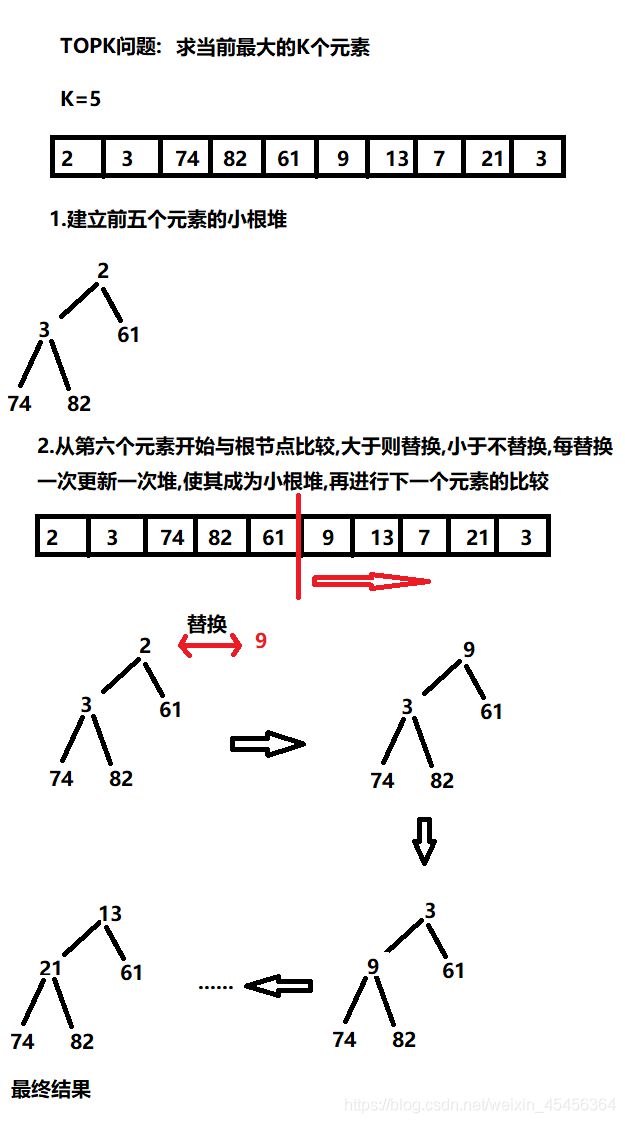
代码实现

public class TopKWithMinHeap {
     
    public static void main(String[] args) {
     
        int k = 5;
        int[] num = {
     2,3,74,82,61,9,13,7,21,3};
        BuildMinHeap(num, 0,k-1);
        for(int i = k; i<num.length; i++){
     
            if(num[i] > num[0]){
     
                swap(num, 0, i);//K下元素与根节点比较交换
            }
            BuildMinHeap(num,0, k-1);//更新小根堆
        }
        System.out.println(Arrays.toString(num));
        System.out.println(num[0]);
    }

    public static void swap(int[] num, int i, int j){
     
        int temp = num[i];
        num[i] = num[j];
        num[j] = temp;
    }

    public static void BuildMinHeap(int[] elem, int root,int len) {
     
        int parent = root;
        int child = 2 * parent + 1;
        while (child < len) {
     

            if (child + 1 < len && elem[child] > elem[child + 1]) {
     
                child = child + 1;
            }
            if (elem[child] < elem[parent]) {
     
                int t = elem[child];
                elem[child] = elem[parent];
                elem[parent] = t;
                parent = child;
                child = 2 * parent + 1;
            }
            if (elem[child] > elem[parent]) {
     
                break;
            }
        }
    }
}