二维路径规划问题--蚁群算法 超详细

路径规划算法

路径规划算法是指在有障碍物的工作环境中寻找一条从起点到终点的、无碰撞地绕过所
有障碍物的运动路径。路径规划算法较多,大体上可分为全局路径规划算法和局部路径规划
算法两类。其中，全局路径规划方法包括位形空间法、广义锥方法、顶点图像法.栅格划归法﹔
局部路径规划算法主要有人工势场法等。

MAKLINK图论

MAKLINK图论可以建立二维路径规划的空间模型,MAKLINK图论通过生成大量的
MAKLINK线构造二维路径规划可行空间,MAKLINK线定义为两个障碍物之间不与障碍物
相交的顶点之间的连线，以及障碍物顶点与边界相交的连线。典型MAKLINE图形如图
所示。

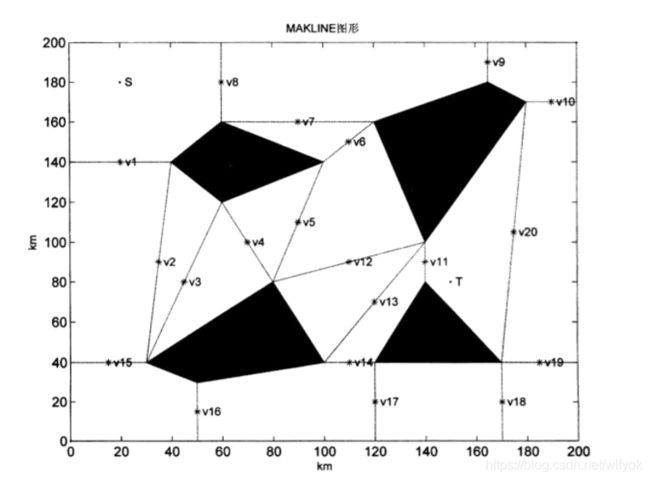
在MAKLINK图上存在↓条自由连接线，连接线的中点依次为v，，…,u,连接所有
MAKLINK线的中点加上始点S和终点T构成用于初始路径规划的无向网络图。

dijkstra算法

dijkstra算法是典型的单源最短路径算法,用于计算非负权值图中一个节点到其他所有节
点的最短路径,其基本思想是把带权图中所有节点分为两组，第1组包括已确定最短路径的节
点,第⒉组为未确定最短路径的节点。按最短路径长度递增的顺序逐个把第⒉组的节点加人
第1组中,直到从源点出发可到达的所有节点都包含在第1组中。
dijkstra算法流程如下:
(1）初始化存放未确定最短路径的节点集合V和已确定最短路径的节点集合S,利用带
权图的邻接矩阵arcs初始化原点到其他节点最短路径长度D,如果源点到其他节点有连接
弧，对应的值为连接弧的权值﹐否则对应的值取为极大值。
(2）选择D中的最小值D[i,D[门是源点到点i的最短路径长度,把点i从集合V中取
出并放人集合S中。
(3）根据节点à修改更新数组D中源点到集合V中的节点k对应的路径长度值。
(4）重复步骤(2)与步骤(3)的操作﹐直至找出源点到所有节点的最短路径为止。

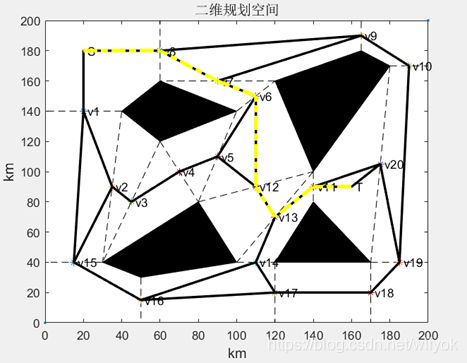
代码与结果

详细代码私聊笔者或评论区留言哦，亲
话不多说，看matlab代码：

% 计算路径距离
cost = ones(size(sign))*10000;
[n,m] = size(sign);
for i = 1:n
    for j = 1:m
        if sign(i,j) == 1
            cost(i,j) = sqrt(sum(position(i,:)-position(j,:)).^2);
        end
    end
end
% 路径开始点
dist = cost(1,:);               % 节点间路径长度
s = zeros(size(dist));          % 节点经过的标志
s(1) = 1;                       
dist(1) = 0;
path = zeros(size(dist));       % 依次经过的节点
path(1,:) = 1;
% 循环寻找路径点
for num = 2:n
    % 选择路径长度最小点
    mindist = 10000;
    for i = 1:length(dist)
        if s(i) == 0
            if dist(i) < mindist
                mindist = dist(i);
                u = i;
            end
        end
    end
    % 更新点点间路径
    s(u) = 1;
    for w = 1:length(dist)
        if s(i) == 0
            if dist(u) + cost(u,w) < dist(w)
                dist(w) = dist(u) + cost(u,w);
                path(w) = u;
            end
        end
    end
end

% 蚁群算法搜索
pathcount = length(path) - 2;   % 经过线段数量
phecacupara = 2;                % 信息素计算参数
phethres = 0.8;                 % 信息素选择阈值
pheuppare = [0.1 0.0003];       % 信息素更新参数
qfz = zeros(pathcount,10);      % 其启发值
phepara = ones(pathcount,10)*pheuppare(2);  % 信息素参数
qfzparal = ones(10,1)*0.5;                  % 启发信息参数
qfzpara2 = 1.1;                             % 启发信息参数
m = 10;                                     % 种群数量
nc = 500;                                   % 循环次数
pathk = zeros(pathcount,m);                 % 搜索结果记录
shortestpath = zeros(1,nc);                 % 进化过程记录
% 初始化
dijpathlen = 0;
vv = zeros(22,2);
vv(1,:) = S;
vv(22,:) = T;
for i = 1:pathcount-1
    dijpathlen = dijpathlen + sqrt((vv(path(i),1)-vv(path(i+1),1))^2-(vv(path(i),2)-vv(path(i+1),2))^2);
end
ll = dijpathlen;
% 经过的链接线
lines = zeros(pathcount,4);
for i = 1:pathcount
    lines(i,1:2) = B(l(path(i+1)-1,1),:);
    lines(i,3:4) = B(l(path(i+1)-1,2),:);
end
% 循环搜索 
for num = 1:nc
    % 蚂蚁迭代寻优依次
    for i = 1:pathcount
        for k = 1:m
            q = rand();
            qfz(i,:) = (qfzpara2-abs((1:10)'/10-qfzpara1))/qfzpara2;
            if q <= phethres
                arg = phepara(i,:).*(qfz(i,:).^phecacupara);
                j = find(arg == max(arg));
                pathk(i,k) = j(1);
            else
                arg = phepara(i,:).*(qfz(i,:).^phecacupara);
                sumarg = sum(arg);
                qq = (q-qo)/(1-qo);
                qtemp = 0;
                j = 1;
                while qtemp < qq
                    qtemp = qtemp + (phepara(i,j)*(qfz(i,j)^phecacupara))/sumarg;
                    j = j + 1;
                end
                j = j - 1;
                pathk(i,j) = j(1);
            end
            % 信息素更新
            phepara(i,j) = (1-pheuppara(1)*phepara(i,j)+pheuppara*pheuppara(2));
        end
    end
    % 计算路径长度
    len = zeros(1,k);
    for k = 1:m
        pstart = S;
        pend = lines(1,1:2) + (lines(1,3:4)-lines(1,1:2))*pathk(1,k)/10;
        for l = 1:pathcount
            len(l,k) = len(l,k) + sqrt(sum((pend-pstart)).^2);
            pstart = pend;
            if l < pathcount
                pend = lines(l+1,1:2) + (lines(l+1,3:4)-lines(l+1,1:2))*pathk(l+1,k)/10;
            end
        end
        pend = T;
        len(l,k) = len(l.k) + sqrt(sum((pend-pstart).^2));
    end
    % 更新信息素
    % 寻找最短路径
    minlen = min(len);
    minlen = minlen(1);
    minant = find(len == minlen);
    minant = minant(1);
    % 更新全局最短路径
    if minlen < ll
        ll = minlen;
    end
    % 更新信息素
    for i = 1:pathcount
        phepara(i,pathk(i,minant)) = (1-pheuppara(1))*phepara(i,pathk(i,minant)) + pheuppara(1)*(1/minlen);
    end
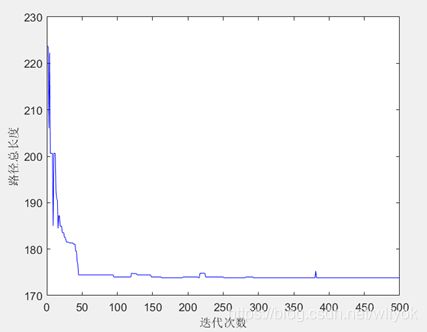
    shortestpath(num) = minlen;
end

详细代码私聊笔者或评论区留言哦，亲