算法问题——动态规划算法理解
动态规划的就是的将原问题拆解成若干子问题,同时保存子问题的答案,使得每个子问题只求解一次 ,最终获得原问题的答案。
动态规划是一种自下而上的一种的思考:就是这个问题是由于前一个问题+加上当前的问题的而得到的结果。F(i)=x+F(i-x)这样的一种的表达。这样的是一种递归的调用,这样的会占用系统的栈空间的,所以在很多时候是最好不采用这样的一种方式。而记忆化搜索是一种的自上而下的一种的方法来实现的。F(i)+x=F(i+x)的这样的一种表现形式。用小数据问题解决大数据问题。采用的是的数组来记录好当前的转态的一种的。
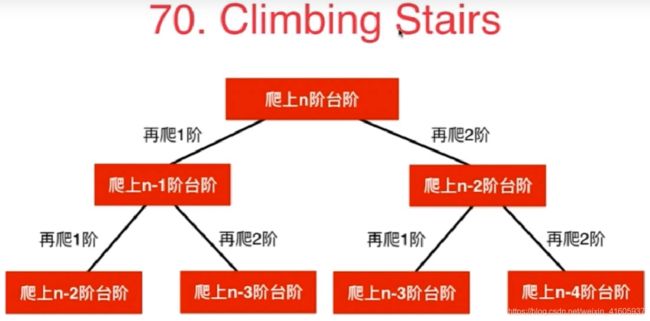
70. 爬楼梯
/**
* 递归函数
*
* @param n
* @return
*/
public int test(int n) {
return calway(n);
}
private int calway(int n) {
if (n == 1 || n == 2) {
return n;
}
return calway(n - 1) + calway(n - 2);
} /**
* 记忆化递归的思想
*
* @param n
* @return
*/
public int solution(int n) {
//这个是记忆的数组 记录是的每一个台阶的方法
int[] memeo = new int[n + 1];
return climbstairs1(n, memeo);
}
private int climbstairs1(int n, int[] memeo) {
if (memeo[n] > 0) {
return memeo[n];
}
if (n == 1 || n == 2) {
memeo[n] = n;
} else {
memeo[n] = climbstairs1(n - 1, memeo) + climbstairs1(n - 2, memeo);
}
return memeo[n];
}
120. 三角形最小路径和
状态的转移方程:dp[i][j]=Math.min(dp[i-1][j-1],dp[i-1][j])+tragle[i][j]
边界的dp[i][0]=dp[i-1][0]+trangle[i][0]
边界的dp[i][j]=dp[i-1][i-1]=trangle[i][i]
/**
* Copyright (C), 2018-2020
* FileName: 最小路径和64
* Author: xjl
* Date: 2020/9/7 12:27
* Description:
*/
package 动态规划问题集合;
import org.junit.Test;
/**
* 写出这个转态的转移方程式
* dp[i][j]=Math.min(dp[i-1][j],dp[i][j-1])+dp[i][j]
*/
public class 最小路径和64 {
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
if (grid == null || m == 0 || n == 0) {
return 0;
}
//1 设置一个数组
int[][] dp = new int[m][n];
//3 确定的边界的时候
dp[0][0] = grid[0][0];
//当列为0的时候的边界
for (int i = 1; i < m; i++) {
dp[i][0] = dp[i - 1][0] + grid[i][0];
}
//当行为0的时候的边界
for (int i = 1; i < n; i++) {
dp[0][i] = dp[0][i - 1] + grid[0][i];
}
//2 状态转移方程
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
}
}
//结果是最后的
return dp[m - 1][n - 1];
}
@Test
public void test() {
int[][] array = {
{1, 3, 1}, {1, 5, 1}, {4, 2, 1}};
int i = minPathSum(array);
System.out.println(i);
}
}120. 三角形最大路径和||
64. 最小路径和
/**
* Copyright (C), 2018-2020
* FileName: 最小路径和64
* Author: xjl
* Date: 2020/9/7 12:27
* Description:
*/
package 动态规划问题集合;
/**
* 写出这个转态的转移方程式 dp[i][j]=Math.min(dp[i-1][j],dp[i][j-1])+dp[i][j]
*/
public class 最小路径和64 {
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
if (grid == null || m == 0 || n == 0) {
return 0;
}
//1 设置一个数组
int[][] dp = new int[m][n];
//3 确定的边界的时候
dp[0][0] = grid[0][0];
//当列为0的时候的边界
for (int i = 1; i < m; i++) {
dp[i][0] = dp[i - 1][0] + grid[i][0];
}
//当行为0的时候的边界
for (int i = 1; i < n; i++) {
dp[0][i] = dp[0][i - 1] + grid[0][i];
}
//2 状态转移方程
for (int i = 1; i < m; i++) {
for (int j = 1; j < n; j++) {
dp[i][j] = Math.min(dp[i - 1][j], dp[i][j - 1]) + grid[i][j];
}
}
//结果是最后的
return dp[m - 1][n - 1];
}
}343. 整数拆分
/**
* Copyright (C), 2018-2020
* FileName: 整数拆分343
* Author: xjl
* Date: 2020/9/7 14:04
* Description:
*/
package 动态规划问题集合;
public class 整数拆分343 {
/**
* 分割两个部分 这是一个递归问题 时间hi超过限制 可能需要采用的记忆化递归的算法
*
* @param n
* @return
*/
static int[] array;
public static int integerBreak(int n) {
array = new int[n + 1];
return test(n);
}
/**
* 这个超过时间限制 也是使用了记忆化搜索的
*
* @param n
* @return
*/
public static int test(int n) {
if (n == 1) {
return 1;
}
if (array[n] != 0) {
return array[n];
}
int res = -1;
//能分割多少的中的方法嗯?
for (int i = 1; i <= n - 1; i++) {
res = Math.max(res, Math.max(i * (n - i), i * test(n - i)));
}
return res;
}
/**
* 记忆化搜索
*
* @param n
* @return
*/
public static int integerBreak1(int n) {
array = new int[n + 1];
array[1] = 1;
for (int i = 2; i <= n; i++) {
//求解array[i] 将 i 进行分割 j i-j这的两个
for (int j = 1; j <= i - 1; j++) {
// j+(i-j)
//计算 i的分割的最大的值保留 array[i - j]前面已经计算出来了所以是
array[i] = Math.max(Math.max(j * (i - j), j * array[i - j]), array[i]);
}
}
return array[n];
}
public static void main(String[] args) {
int i = integerBreak1(30);
System.out.println(i);
}
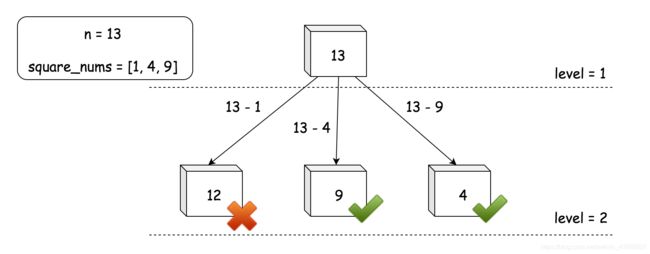
}279. 完全平方数
正如上述贪心算法的复杂性分析种提到的,调用堆栈的轨迹形成一颗 N 元树,其中每个结点代表 is_divided_by(n, count) 函数的调用。基于上述想法,我们可以把原来的问题重新表述如下:
给定一个 N 元树,其中每个节点表示数字 n 的余数减去一个完全平方数的组合,我们的任务是在树中找到一个节点,该节点满足两个条件:
(1) 节点的值(即余数)也是一个完全平方数。
(2) 在满足条件(1)的所有节点中,节点和根之间的距离应该最小。
在前面的方法3中,由于我们执行调用的贪心策略,我们实际上是从上到下逐层构造 N 元树。我们以 BFS(广度优先搜索)的方式遍历它。在 N 元树的每一级,我们都在枚举相同大小的组合。
遍历的顺序是 BFS,而不是 DFS(深度优先搜索),这是因为在用尽固定数量的完全平方数分解数字 n 的所有可能性之前,我们不会探索任何需要更多元素的潜在组合。
//这样的问题还有一个特点就是都是1--n的一个效果。
public int numSquares1(int n) {
int[] dp = new int[n + 1]; // 默认初始化值都为0
for (int i = 1; i <= n; i++) {
dp[i] = i; // 最坏的情况就是每次+1 就是采用的是的全部是1的这样的方式
for (int j = 1; i - j * j >= 0; j++) {
//每次去看这个j表示的是的平方数 一定是小于这i的
dp[i] = Math.min(dp[i], dp[i - j * j] + 1); // 动态转移方程
}
}
return dp[n];
}class Solution {
public int numSquares(int n) {
ArrayList square_nums = new ArrayList();
for (int i = 1; i * i <= n; ++i) {
square_nums.add(i * i);
}
Set queue = new HashSet();
queue.add(n);
int level = 0;
while (queue.size() > 0) {
level += 1;
Set next_queue = new HashSet();
for (Integer remainder : queue) {
for (Integer square : square_nums) {
if (remainder.equals(square)) {
return level;
} else if (remainder < square) {
break;
} else {
next_queue.add(remainder - square);
}
}
}
queue = next_queue;
}
return level;
}
} 91. 解码方法
"12321"的解码数 = "1232"的解码数 + "123"的解码数,当然也要考虑后1、2位能否构成合法的字母。
/**
* Copyright (C), 2018-2020
* FileName: 解码方法91
* Author: xjl
* Date: 2020/9/8 14:04
* Description:
*/
package 动态规划问题集合;
import java.util.HashMap;
public class 解码方法91 {
public int numDecodings(String s) {
return getAns(s, 0);
}
private int getAns(String s, int start) {
//划分到了最后返回 1
if (start == s.length()) {
return 1;
}
//开头是 0,0 不对应任何字母,直接返回 0
if (s.charAt(start) == '0') {
return 0;
}
//得到第一种的划分的解码方式
int ans1 = getAns(s, start + 1);
int ans2 = 0;
//判断前两个数字是不是小于等于 26 的
if (start < s.length() - 1) {
int ten = (s.charAt(start) - '0') * 10;
int one = s.charAt(start + 1) - '0';
if (ten + one <= 26) {
ans2 = getAns(s, start + 2);
}
}
return ans1 + ans2;
}
public int numDecodings2(String s) {
int len = s.length();
int[] dp = new int[len + 1];
//将递归法的结束条件初始化为 1
dp[len] = 1;
//最后一个数字不等于 0 就初始化为 1
if (s.charAt(len - 1) != '0') {
dp[len - 1] = 1;
}
for (int i = len - 2; i >= 0; i--) {
//当前数字时 0 ,直接跳过,0 不代表任何字母
if (s.charAt(i) == '0') {
continue;
}
int ans1 = dp[i + 1];
//判断两个字母组成的数字是否小于等于 26
int ans2 = 0;
int ten = (s.charAt(i) - '0') * 10;
int one = s.charAt(i + 1) - '0';
if (ten + one <= 26) {
ans2 = dp[i + 2];
}
dp[i] = ans1 + ans2;
}
return dp[0];
}
public int numDecodings3(String s) {
HashMap memoization = new HashMap<>();
return getAns(s, 0, memoization);
}
private int getAns(String s, int start, HashMap memoization) {
//表示的是的s的长度 到了最后的一个分割位置
if (start == s.length()) {
return 1;
}
//如果还第一个位置为0 表示的是的0
if (s.charAt(start) == '0') {
return 0;
}
//判断之前是否计算过
int m = memoization.getOrDefault(start, -1);
if (m != -1) {
return m;
}
int ans1 = getAns(s, start + 1, memoization);
int ans2 = 0;
if (start < s.length() - 1) {
int ten = (s.charAt(start) - '0') * 10;
int one = s.charAt(start + 1) - '0';
if (ten + one <= 26) {
ans2 = getAns(s, start + 2, memoization);
}
}
//将结果保存
memoization.put(start, ans1 + ans2);
return ans1 + ans2;
}
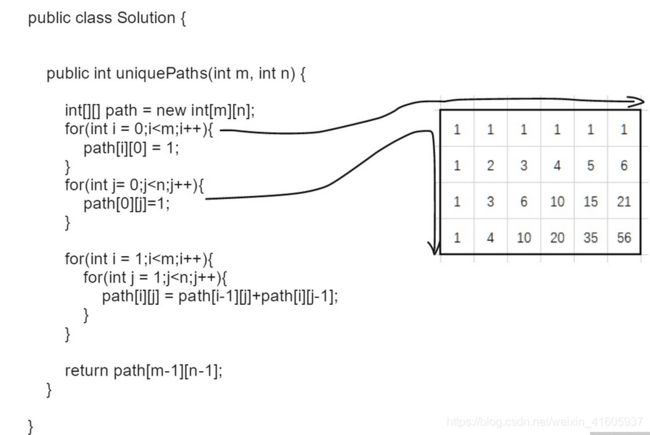
} 62. 不同路径
public int uniquePaths(int m, int n) {
//d[i][j]: start->(i,j) 一共有多少个uniqueunique paths
//d[i][j]=dp[i-1][j]+d[i][j-1]
//d[0][0]=1
int[][] dp=new int[m][n];
dp[0][0]=1;
for(int i=0;i0){
dp[i][j]+=dp[i-1][j];
}
if(j>0){
dp[i][j]+=dp[i][j-1];
}
}
}
return dp[m-1][n-1];
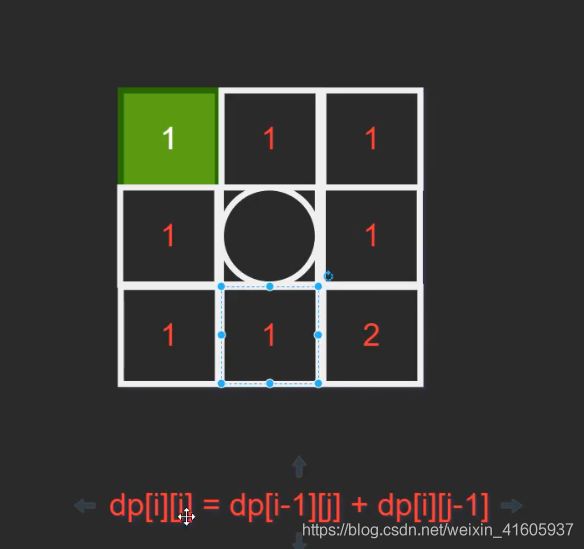
} 63. 不同路径 II
/**
* 一种的直接从(0,0)开始的计算 然后按照这个每一行的计算
* @param obstacleGrid
* @return
*/
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
int m = obstacleGrid.length;
int n = obstacleGrid[0].length;
int[][] dp = new int[m][n];
dp[0][0] = 1;
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (obstacleGrid[i][j] == 1) {
dp[i][j] = 0;
} else {
if (j > 0) {
dp[i][j] += dp[i][j - 1];
}
if (i > 0) {
dp[i][j] += dp[i - 1][j];
}
}
}
}
return dp[m - 1][n - 1];
}/**
*一种的方法是:开始的把两边的开始 * 开始的从(1,1) 开始的的时候计算
*/
class Solution {
public int uniquePathsWithObstacles(int[][] ob) {
int m = ob.length;
int n = ob[0].length;
if(m == 0 || n == 0) return 0;
// `ob[i][j] == 1`表示无障碍物,`dp[i][j] = dp[i - 1][j] + d[i][j - 1]`
int[][] dp = new int[m][n];
// 初始化
// 第0行和第0列分别遍历,赋值为1;
// 如果碰到障碍物,从这个点之后全为0,因为碰到障碍物,之后都不可达了。
for(int i = 0; i < m; i++) {
if(ob[i][0] == 1) break;
else dp[i][0] = 1;
}
for(int i = 0; i < n; i++) {
if(ob[0][i] == 1) break;
else dp[0][i] = 1;
}
for(int i = 1; i < m; i++){
for(int j = 1; j < n; j++){
// `ob[i][j] == 1`表示有障碍物,直接令`dp[i][j] = 0`;
if(ob[i][j] == 1) dp[i][j] = 0;
// `ob[i][j] == 0`表示无障碍物,`dp[i][j] = dp[i - 1][j] + d[i][j - 1]`
else dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
}
}
return dp[m - 1][n - 1];
}
}198. 打家劫舍
首先考虑最简单的情况。如果只有一间房屋,则偷窃该房屋,可以偷窃到最高总金额。如果只有两间房屋,则由于两间房屋相邻,不能同时偷窃,只能偷窃其中的一间房屋,因此选择其中金额较高的房屋进行偷窃,可以偷窃到最高总金额。
如果房屋数量大于两间,应该如何计算能够偷窃到的最高总金额呢?对于第 k (k>2)k~(k>2)k (k>2) 间房屋,有两个选项:
偷窃第 kkk 间房屋,那么就不能偷窃第 k−1k-1k−1 间房屋,偷窃总金额为前 k−2k-2k−2 间房屋的最高总金额与第 kkk 间房屋的金额之和。
不偷窃第 kkk 间房屋,偷窃总金额为前 k−1k-1k−1 间房屋的最高总金额。
在两个选项中选择偷窃总金额较大的选项,该选项对应的偷窃总金额即为前 kkk 间房屋能偷窃到的最高总金额。
用 dp[i]dp[i]dp[i] 表示前 iii 间房屋能偷窃到的最高总金额,那么就有如下的状态转移方程:
class Solution {
public int rob(int[] nums) {
if (nums == null || nums.length == 0) {
return 0;
}
int length = nums.length;
if (length == 1) {
return nums[0];
}
int[] dp = new int[length];
dp[0] = nums[0];
dp[1] = Math.max(nums[0], nums[1]);
for (int i = 2; i < length; i++) {
dp[i] = Math.max(dp[i - 2] + nums[i], dp[i - 1]);
}
return dp[length - 1];
}
}/**
* Copyright (C), 2018-2020
* FileName: 打劫1
* Author: xjl
* Date: 2020/9/8 15:58
* Description:
*/
package 动态规划问题集合;
import java.util.Arrays;
public class 打劫1 {
public static int rob(int[] nums) {
return testrob(nums, 0);
}
/**
* 考虑的是的nums[index…… nums.size()]这个范围的所有的房子
*
* @param nums
* @param index
* @return
*/
public static int testrob(int[] nums, int index) {
if (index >= nums.length) {
return 0;
}
//开始抢劫这个房子以后的所有房子
int res = 0;
for (int i = index; i < nums.length; i++) {
res = Math.max(res, nums[i] + testrob(nums, index + 2));
}
return res;
}
/**
* 采用的是记忆化搜索的方法来实现
* @param nums
* @param index
* @return
*/
static int[] memo;
public static int rob1(int[] nums) {
memo = new int[nums.length];
Arrays.fill(memo, -1);
return testrob2(nums, 0);
}
public static int testrob2(int[] nums, int index) {
if (index >= nums.length) {
return 0;
}
//判断时候有值 如果有值就不需要计算了 如果是没有就需要的是的计算
if (memo[index] != -1) {
return memo[index];
}
//开始抢劫这个房子以后的所有房子
int res = 0;
for (int i = index; i < nums.length; i++) {
res = Math.max(res, nums[i] + testrob2(nums, i + 2));
}
//每一次将这个保留这个转态
memo[index] = res;
return res;
}
}
public int rob4(int[] nums) {
if (nums.length == 0) {
return 0;
}
// 子问题:
// f(k) = 偷 [0..k) 房间中的最大金额
// f(0) = 0
// f(1) = nums[0]
// f(k) = max{ rob(k-1), nums[k-1] + rob(k-2) }
int N = nums.length;
//表示的是的最大的数字
int[] dp = new int[N + 1];
dp[0] = 0;
dp[1] = nums[0];
for (int k = 2; k <= N; k++) {
dp[k] = Math.max(dp[k - 1], nums[k - 1] + dp[k - 2]);
}
return dp[N];
}213. 打家劫舍 II
环状排列意味着第一个房子和最后一个房子中只能选择一个偷窃,因此可以把此环状排列房间问题约化为两个单排排列房间子问题:
在不偷窃第一个房子的情况下(即 nums[1:]nums[1:]nums[1:]),最大金额是 p1,p1 ;
在不偷窃最后一个房子的情况下(即 nums[:n−1]nums[:n-1]nums[:n−1]),最大金额是 p2,p2 。
综合偷窃最大金额: 为以上两种情况的较大值,即 max(p1,p2) 。
import java.util.Arrays;
public class 打劫2 {
public int rob(int[] nums) {
if (nums.length == 0) return 0;
if (nums.length == 1) return nums[0];
return Math.max(rob4(Arrays.copyOfRange(nums, 0, nums.length - 1)),rob4(Arrays.copyOfRange(nums, 1, nums.length)));
}
public int rob4(int[] nums) {
if (nums.length == 0) {
return 0;
}
// 子问题:
// f(k) = 偷 [0..k) 房间中的最大金额
// f(0) = 0
// f(1) = nums[0]
// f(k) = max{ rob(k-1), nums[k-1] + rob(k-2) }
int N = nums.length;
//表示的是的最大的数字
int[] dp = new int[N + 1];
dp[0] = 0;
dp[1] = nums[0];
for (int k = 2; k <= N; k++) {
dp[k] = Math.max(dp[k - 1], nums[k - 1] + dp[k - 2]);
}
return dp[N];
}
}
337. 打家劫舍 III
/**
* Copyright (C), 2018-2020
* FileName: 打劫3
* Author: xjl
* Date: 2020/9/13 13:41
* Description:
*/
package 动态规划问题集合;
public class 打劫3 {
public class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode(int x) {
val = x;
}
}
// 树的后序遍历
public int rob(TreeNode root) {
int[] res = dfs(root);
return Math.max(res[0], res[1]);
}
private int[] dfs(TreeNode node) {
if (node == null) {
return new int[]{0, 0};
}
// 分类讨论的标准是:当前结点偷或者不偷
// 由于需要后序遍历,所以先计算左右子结点,然后计算当前结点的状态值
int[] left = dfs(node.left);
int[] right = dfs(node.right);
// dp[0]:以当前 node 为根结点的子树能够偷取的最大价值,规定 node 结点不偷
// dp[1]:以当前 node 为根结点的子树能够偷取的最大价值,规定 node 结点偷
int[] dp = new int[2];
dp[0] = Math.max(left[0], left[1]) + Math.max(right[0], right[1]);
dp[1] = node.val + left[0] + right[0];
return dp;
}
}
309. 最佳买卖股票时机含冷冻期
剑指 Offer 63. 股票的最大利润
901. 股票价格跨度
121. 买卖股票的最佳时机
122. 买卖股票的最佳时机 II
123. 买卖股票的最佳时机 III
188. 买卖股票的最佳时机 IV