python编程——007背包问题leetcode132分割回文字串2
一、动态规划与0/1背包问题
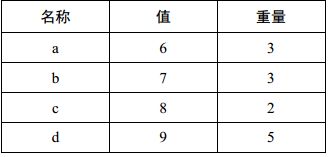
在python编程导论这本书中是这样引入背包问题的一个小偷入室盗窃发现的物品有几种,他们价值不同但是重量也不同,而且背包空间有,那么该带走什么才能利益最大化。这就涉及到最优解问题。
用贪婪算法的话,时间复杂度为贪婪算法的时间复杂度是O(nlog(n))无法确保解是最优解。
那么如何来规范定义0/1背包问题:
个物品都可以用一个值对<价值, 重量>表示;
1) 背包能够容纳的物品总重量不能超过w;
2)长度为n的向量I表示一个可用的物品集合,向量中的每个元素都代表一个物品;
3)长度为n的向量V表示物品是否被窃贼带走。如果V[i] = 1,则物品I[i]被带走;如果V[i] = 0,则物品I[i]没有被带走;
4)目标是找到一个V,使得: ∑ i = 0 n − 1 V [ i ] ∗ I [ i ] . v a l u e \sum_{i=0}^{n-1}V[i]*I[i].value ∑i=0n−1V[i]∗I[i].value的值最大,并满足以下约束条件: ∑ i = 0 n − 1 V [ i ] ∗ I [ i ] . w e i g h t ≤ w \sum_{i=0}^{n-1}V[i]*I[i].weight \leq w ∑i=0n−1V[i]∗I[i].weight≤w
暴力法,枚举所有可能的组合,去除掉超过重量的组合,在剩余组合里面找价值最大的,时间复杂度为 O ( n ∗ 2 n ) O(n*2^n) O(n∗2n)
我们从待定物品中选择出一个,如果背
包放得下这个物品,就建立一个节点,反映出选择带走这个物品的后果。按照惯例,我们将这个
节点作为左子节点,而用右子节点表示不带走这个物品的后果。以递归方式不断执行这个过程,
直到背包被装满或者没有待定物品。因为每条边都表示一个决策(带走或不带走某个物品),所
以这种树称为决策树。在背包能够容纳的最大重量为5的假设之下,可以确定应该带走哪
些物品。树的根节点(节点0)有一个标签<{}, [a, b, c, d], 0, 5>,表示没有选择物品,所
有物品都处于待定状态,带走的物品总值为0,背包剩余空间还能容纳的重量为5。节点1表示物
品a被带走,物品[b, c, d]处于待定状态,带走的物品总值为6,背包还能容纳2的重量。节点1
没有左子节点,因为物品b的重量为3,不能放在背包中。

class Item(object):
def __init__(self, n, v, w):
self.name = n
self.value = v
self.weight = w
def getName(self):
return self.name
def getValue(self):
return self.value
def getWeight(self):
return self.weight
def __str__(self):
result = '<' + self.name + ', ' + str(self.value)+ ', ' + str(self.weight) + '>'
return result
def value(item):
return item.getValue()
def weightInverse(item):
return 1.0/item.getWeight()
def density(item):
return item.getValue()/item.getWeight()
def maxVal(toConsider, avail):
"""假设toConsider是一个物品列表, avail表示重量
#返回一个元组表示0/1背包问题的解,包括物品总价值和物品列表"""
if toConsider == [] or avail == 0:
result = (0, ())
elif toConsider[0].getWeight() > avail:
#探索右侧分支
result = maxVal(toConsider[1:], avail)
else:
nextItem = toConsider[0]
#探索左侧分支
withVal, withToTake = maxVal(toConsider[1:],avail - nextItem.getWeight())
withVal += nextItem.getValue()
#探索右侧分支
withoutVal, withoutToTake = maxVal(toConsider[1:], avail)
#选择更好的分支
if withVal > withoutVal:
result = (withVal, withToTake + (nextItem,))
else:
result = (withoutVal, withoutToTake)
return result
做法
class Solution(object):
def minCut(self, s):
"""
:type s: str
:rtype: int
"""
#p[j][i] 判断j-i是否是回文序列 dp[i]0~i的最少分割
ls=len(s)
dp=[0]*(ls+1)
dp[0]=-1
p=[[False]*ls for i in range(ls)]
for i in range(ls):
dp[i+1]=i
for i in range(ls):
for j in range(i+1):
if s[j]==s[i] and ((i-j<2) or p[j+1][i-1]):
p[j][i]=True
dp[i+1]=min(1+dp[j],dp[i+1])
return dp[ls]
思路
如果s[left:right]是回文,而且s[:left]也是回文的话,那么s[:right]即是一个分割。同理如果dp[left:right]是最小回文分割,并且dp[:left]也是最小回文分割,那么我们有dp[:right]=dp[left:right]+dp[:left]。为了方便遍历进行,把dp[left:right]设置为1,即s[left:right]是回文。,再增加一个判断s[left:right]是否是回文序列的二维数组。
