算法系列:并查集和前缀树
前言
本篇归纳并查集和前缀树
1、并查集
并查集(union-find)主要功能
- Find:确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。
- Union:将两个子集合并成同一个集合。
本想自己总结下
然后发现了一篇
我愿称之为绝活
并查集详解
下面就看些实例吧
朋友圈
leet上547题
班上有 N 名学生。其中有些人是朋友,有些则不是。他们的友谊具有是传递性。
如果已知 A 是 B 的朋友,B 是 C 的朋友,那么我们可以认为 A 也是 C 的朋友。
所谓的朋友圈,是指所有朋友的集合。
给定一个 N * N 的矩阵 M,表示班级中学生之间的朋友关系。
如果M[i][j] = 1,表示已知第 i 个和 j 个学生互为朋友关系,否则为不知道。
你必须输出所有学生中的已知的朋友圈总数。
class Solution:
def findCircleNum(self, M) -> int:
father = [i for i in range(len(M))]
def find(a):
if father[a] != a: father[a] = find(father[a])
return father[a]
def union(a, b):
father[find(b)] = find(a)
return find(b)
for a in range(len(M)):
for b in range(a):
if M[a][b]: union(a, b)
for i in range(len(M)): find(i)
return len(set(father))
冗余连接
leet上684题
在本问题中, 树指的是一个连通且无环的无向图。
输入一个图,该图由一个有着N个节点 (节点值不重复1, 2, ..., N) 的树及一条附加的边构成。
附加的边的两个顶点包含在1到N中间,这条附加的边不属于树中已存在的边。
结果图是一个以边组成的二维数组。每一个边的元素是一对[u, v] ,满足 u < v,表示连接顶点u 和v的无向图的边。
返回一条可以删去的边,使得结果图是一个有着N个节点的树。
如果有多个答案,则返回二维数组中最后出现的边。
答案边 [u, v] 应满足相同的格式 u < v。
class Solution:
def findRedundantConnection(self, edges: List[List[int]]) -> List[int]:
p = [*range(len(edges) + 1)] #并查集元素初始化
def f(x):
if p[x] != x: #递归修改所属集合
p[x] = f(p[x])
return p[x]
for x, y in edges: #遍历边
px, py = f(x), f(y)
if px != py: #检查集合,如果集合不同就合并
p[py] = px
else:
return [x, y] #集合相同就返回答案
账户合并
leet上721题
给定一个列表 accounts,每个元素 accounts[i] 是一个字符串列表,其中第一个元素 accounts[i][0] 是 名称 (name),其余元素是 emails 表示该帐户的邮箱地址。
现在,我们想合并这些帐户。如果两个帐户都有一些共同的邮件地址,则两个帐户必定属于同一个人。
请注意,即使两个帐户具有相同的名称,它们也可能属于不同的人,因为人们可能具有相同的名称。
一个人最初可以拥有任意数量的帐户,但其所有帐户都具有相同的名称。
合并帐户后,按以下格式返回帐户:每个帐户的第一个元素是名称,其余元素是按顺序排列的邮箱地址。accounts 本身可以以任意顺序返回。
class Solution:
def accountsMerge(self, accounts: List[List[str]]) -> List[List[str]]:
dic = {
}
def find(x):
dic.setdefault(x, x)
if x != dic[x]:
dic[x] = find(dic[x])
return dic[x]
def union(a, b):
dic[find(a)] = find(b)
res = collections.defaultdict(list)
email_to_name = {
}
for account in accounts:
for i in range(1, len(account)):
email_to_name[account[i]] = account[0]
if i < len(account) - 1: union(account[i], account[i + 1])
for email in email_to_name:
res[find(email)].append(email)
return [[email_to_name[value[0]]] + sorted(value) for value in res.values()]
由斜杠划分区域
leet上959题
在由 1 x 1 方格组成的 N x N 网格 grid 中,每个 1 x 1 方块由 /、\ 或空格构成。这些字符会将方块划分为一些共边的区域。
(请注意,反斜杠字符是转义的,因此 \ 用 "\\" 表示。)。
返回区域的数目。
class Solution:
def regionsBySlashes(self, grid: List[str]) -> int:
N = len(grid)
parent = [i for i in range(4 * N * N)] # 开始的时候每个节点的帮主都是自己
def find(parent, x): # 寻找每个节点的帮主
if parent[x] == x:
return parent[x]
return find(parent, parent[x])
def union(parent, x, y): # 两个人相遇, 那么各自去找教主,教主对决
x_root = find(parent, x)
y_root = find(parent, y)
if x_root != y_root: # 教主不同
parent[x_root] = y_root # 对决赢的成为新教主
def union_find(grid):
for r, row in enumerate(grid):
for c, val in enumerate(row):
top = 4 * (r * N + c)
if val in ['/', ' ']:
union(parent, top + 0, top + 1)
union(parent, top + 2, top + 3)
if val in ['\\', ' ']:
union(parent, top + 0, top + 2)
union(parent, top + 1, top + 3)
if r + 1 < N:
union(parent, top + 3, top + (4 * N) + 0)
if r - 1 >= 0: # 这部分其实是多于的
union(parent, top + 0, top - (4 * N) + 3)
if c + 1 < N:
union(parent, top + 2, top + 4 + 1)
if c - 1 >= 0: # 这部分其实也是多于的
union(parent, top + 1, top - 4 + 2)
return sum(parent[x] == x for x in range(4 * N * N))
return union_find(grid)
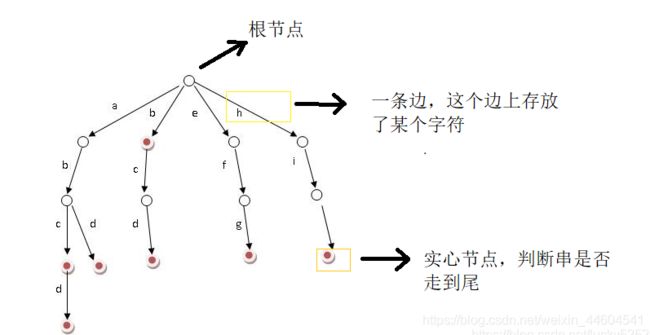
2、前缀树
- 树节点:树的节点中存放的是状态,判断字符串是否走到结尾了
- 边:每个边上有一个字符,从根开始的路径上的字符组成了串
一个前缀树的实现如下
包含 insert, search 和 startsWith 三个操作
from collections import defaultdict
class TrieNode: #节点构造
def __init__(self):
self.children = defaultdict(TrieNode)
self.word = False
class Trie:
def __init__(self):
"""
Initialize your data structure here.
"""
self.root = TrieNode()
def insert(self, word: str) -> None:
"""
Inserts a word into the trie.
"""
tmp = self.root
for a in word:
tmp = tmp.children[a]
tmp.word = True
def search(self, word: str) -> bool:
"""
Returns if the word is in the trie.
"""
tmp = self.root
for a in word:
if a not in tmp.children:
return False
tmp = tmp.children[a]
if tmp.word:
return True
return False
def startsWith(self, prefix: str) -> bool:
"""
Returns if there is any word in the trie that starts with the given prefix.
"""
tmp = self.root
for a in prefix:
if a not in tmp.children:
return False
tmp = tmp.children[a]
return True
# Your Trie object will be instantiated and called as such:
# obj = Trie()
# obj.insert(word)
# param_2 = obj.search(word)
# param_3 = obj.startsWith(prefix)
下面看些实例
添加与搜索单词
leet上211题
如果数据结构中有任何与word匹配的字符串,则bool search(word)返回true,否则返回false。
单词可能包含点“。” 点可以与任何字母匹配的地方。
请你设计一个数据结构,支持 添加新单词 和 查找字符串是否与任何先前添加的字符串匹配 。
实现词典类 WordDictionary :
WordDictionary() 初始化词典对象
void addWord(word) 将 word 添加到数据结构中,之后可以对它进行匹配
bool search(word) 如果数据结构中存在字符串与 word 匹配,则返回 true ;否则,返回 false 。word 中可能包含一些 '.' ,每个 . 都可以表示任何一个字母。
class WordDictionary:
def __init__(self):
"""
Initialize your data structure here.
"""
from collections import defaultdict
self.lookup = {
}
def addWord(self, word: str) -> None:
"""
Adds a word into the data structure.
"""
tree = self.lookup
for a in word:
tree = tree.setdefault(a, {
})
tree["#"] = {
}
def search(self, word: str) -> bool:
"""
Returns if the word is in the data structure. A word could contain the dot character '.' to represent any one letter.
"""
def helper(word, tree):
if not word:
if "#" in tree:
return True
return False
if word[0] == ".":
for t in tree:
if helper(word[1:], tree[t]):
return True
elif word[0] in tree:
if helper(word[1:], tree[word[0]]):
return True
return False
return helper(word, self.lookup)
键值映射
leet上677题
实现一个 MapSum 类里的两个方法,insert 和 sum。
对于方法 insert,你将得到一对(字符串,整数)的键值对。字符串表示键,整数表示值。如果键已经存在,那么原来的键值对将被替代成新的键值对。
对于方法 sum,你将得到一个表示前缀的字符串,你需要返回所有以该前缀开头的键的值的总和。
from collections import defaultdict
class TrieNode:
def __init__(self):
self.children = defaultdict(TrieNode)
self.val = 0
class MapSum:
def __init__(self):
"""
Initialize your data structure here.
"""
self.root = TrieNode()
def insert(self, key: str, val: int) -> None:
node = self.root
path = [node]
for char in key:
node = node.children[char]
path.append(node)
diff = node.val - sum([child.val for child in node.children.values()])
for node in path:
node.val += val - diff
def sum(self, prefix: str) -> int:
node = self.root
for char in prefix:
node = node.children[char]
return node.val
结语
并查集和前缀树都是很有用很秀的算法