数据结构之图

图

图的定义：是一种较线性结构和树更为复杂的数据结构，图中任意两个结点之间都可以直接相关。顶点之

间的关系是多对多的。

图是一个二元组：G=(V,E)，v定点集合，E边集合

图分为无向图和有向图。

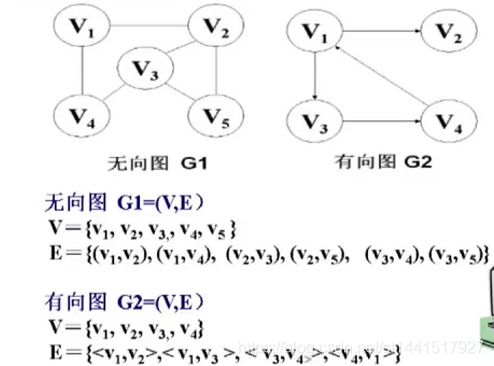
注意有向图边的集合元素之间是用<>包起来的。

顶点：图中的数据元素。

边：两个顶点之间的关系。

无向图中的顶点偶对（例如：（）v1，v2）边）（边）是无序的。

有向图的图中顶点偶对（弧）是有序的。

完全图和有向完全图：

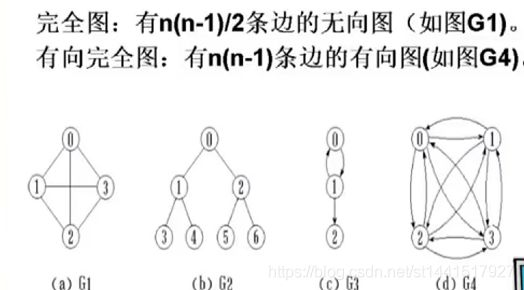
完全图：如G：4个顶点，4*（4-1）/2=6，正好6条边。

有向完全图：如G4:4个顶点。4*（4-1）=12，正好12条边。任意两个顶点之间都有两条不同向的边。

稀疏图：有很少的边或者弧的图。

稠密图：有很多的边或者弧（有向图里面边也叫作弧）的图。

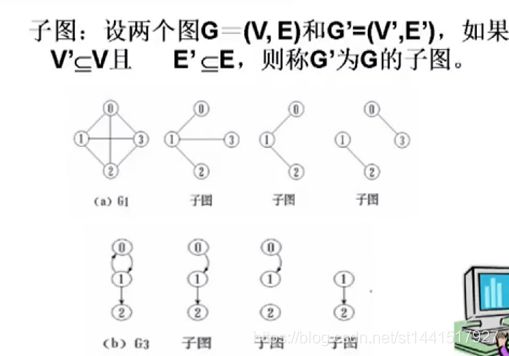
子图：第二个图的所有顶点都包含在第一个图中的顶点集之中，同时第二个图的所有边都在第一个图中的边

集合中。

权和网：

权（Weight）：与图的边相关的数值。

网（Network）：带权的图。

邻接点：

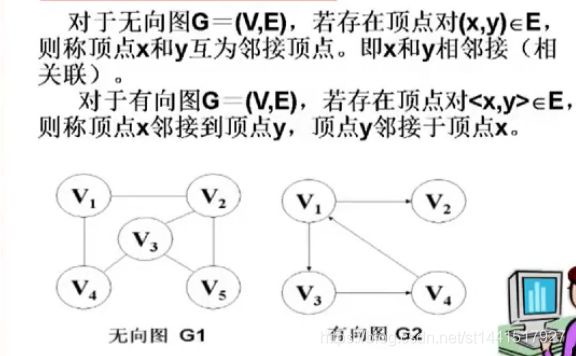
无向图：两个存在于主图顶点集合当中的顶点之间相互关联，这种称为v1和v2相邻接。

有向图：起点邻接于终点。

两种图的邻接关系不同。

顶点的度：在无向图中，和该顶点相关联的边的数目称为顶点的度。

TD：表示指定顶点的度。

有向图中：以x顶点为尾的弧的数目称为顶点x的出度，以x为头的弧的数目称为顶点x的入度。

有向图中：顶点的度等于该顶点的入度和出度之和。

路径与路径长度。

路径：在图中，若从顶点x除法，经过一些顶点v1、v2、…、vm到达顶点y。则称为顶点序列为（x、v1、

v2、…、vm、y）为顶点x到顶点y的路径。

路径长度：

①非带权图的路径长度是指此路径上砭的条数，

②带权图的路径长度是指路径上各边的权之和。

简单路径：序列中的顶点不重复出现的路径。

回路（环）：第一个顶点和最后一个顶点相同的路径。

简单回路（环）：除第一个和最后一个顶点，其余顶点不重复出现的路径。

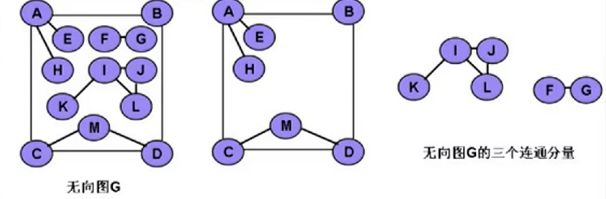
连通图与连通分量：

连通：在无向图中，如果从x到y存在路径，则称为x和y是连通的。

连通图：无向图G中如果任意两个顶点x、y之间都是连通的，则称为G是连通图。

例如：这个图是连通图，但不是完全图，每个顶点之间都存在路径。

连通分量：无向图中的 极大连通子图。

第一个图是主图：后面三个都是第一个图的连通子图。

极大连通子图：将主图中的任意一个不在子图中的任意顶点放在子图当中，将导致子图不再是连通图。

例如：D、E两个顶点，将其他的任意顶点放在这两个顶点的子图当中，都会导致子图不是连通图，所以这个

虽然是两个顶点，但是依然是个连通子图。

有向图中的强连通图和连通分量：

强连通图：有向图G中任意两个顶点x、y之间都是相互科大的。称为G是强连通图。两个顶点之间都有互相指

向的弧。

连通分量：有向图中的极大连通子图。

例如第二个，就不是强连通图。

有向图的极大连通子图：

最后一个图的两部分都是第二个图的连通分量。也就是极大连通子图。

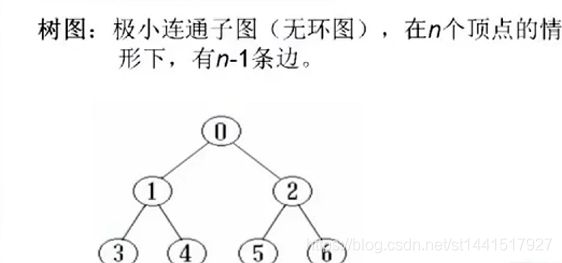
图的存储结构：

图需要存储的信息：顶点和边；

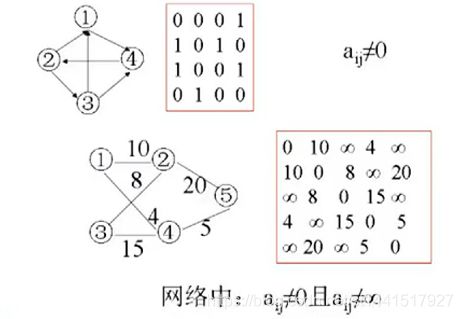
1、邻接矩阵：表示顶点之间相邻关系的矩阵。里面的值不是1就是0

两个顶点可达为1，不可达为0----<>表示边元素。

有向图中，图中有n条边，那么对应的矩阵图中有n个1.

无向图中，图中有n条边，那么对应的矩阵图中有2n个1，而且无向图中的 矩阵图是对称的。

网的邻接矩阵：


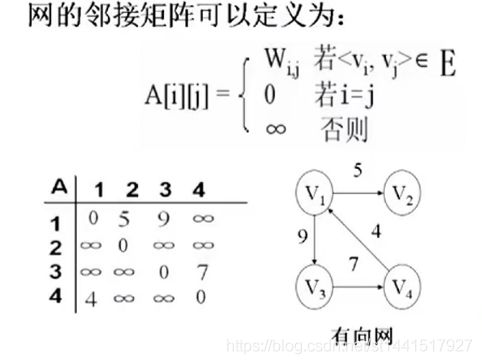
性质2中，非零元素的个数也就是边的个数。自然而然也就是这个顶点的度。
性质3：行元素起始。所以每一行的非零元素的个数就是这一行顶点的出度。列元素为终，所以每一列的非零元素的个数就是这一列顶点的入度。
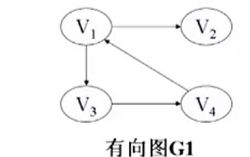
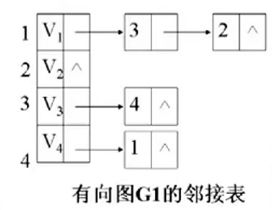
建立邻接表：

有向图和无向图的区别：

无向图的话，因为矩阵是对称的，所以需要在赋值语句中添加一条：a[j][i]=1

判断通过矩阵两个顶点之间有没有边：

2、邻接链表

后面的结点中的数值是对应结点的数组下标

①拿一个数组存放图中所有的顶点。

无向图：

数组中的每一个元素为一个结构体指针的链表，链表中指针的指向表示边。

有向图：

也是拿数组存储图中的结点。


有向网络：

也就是在结点中添加了一个权的变量。

数组中存放的是头结点：

被指向的结点是边结点。

如果是邻接表，那么头结点可以添加一个成员变量空间为记录当前结点的入度。如果是逆邻接表，那么可以

存储对应结点的出度。

算法：

①：权值

vertex：数组下标

②：存储头结点的结构体类型

③：头结点的其他信息。

④：指向边结点的指针，所有是边结点的结构体类型。

输入边的时候将权值一起输入

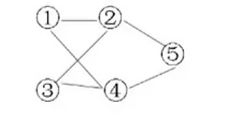
图的遍历：

1、深度优先搜索：

示例：

v1开始，可以先访问v2、或者v3，此处选择v2.

沿着v2访问带v5之后，发现v5没有未被访问的邻结点。所以沿着原路返回，接着查看v8是否存在未被访问的

邻结点。依次下去。

此处序列可能不唯一。

算法描述：

假设g是连通图或者非连通图的一个联通分量，将v0的第一个邻接顶点放在w中。

每一层循环结束之后，都是向上一层返回的过程，上一层会继续判断是否还存在为被访问的邻接顶点。

深度优先搜索是针对于连通图的。

访问非连通图的时候，需要多次重复深度优先搜索。因为有些顶点之间是不可达的。无论从哪个顶点为起始

顶点，都只会发生下面的三种情况中的一种。

如果从当前顶点开始遍历，结束后发现没有遍历到全部的顶点，那么此时需要重新选择一个起始顶点。

重复3次上面遍历，就能将所有的顶点遍历完毕。

因为可能涉及到多个起始顶点，所以不需要知道起始顶点。

这个dfstraverse函数只是确定起始顶点，下面依然调用了上面的dfs函数，传入被需要遍历的图和起始顶点。

此处只会将未被访问过的顶点为起始顶点。

以邻接表为存储结构的图的遍历。

mark数组存放所有顶点状态的数组。

g：存储起始顶点的数组

v：起始顶点的数组下标

依然借用的是dfs函数，只是在寻找起始顶点的时候会有不同。

非递归实现算法：

数组中应该存储结点的值和指针。

需要注意的是：虽然2结点中的指针指向4，并不是2和4之间有边，而是起始顶点1和4之间有边。


算法：

①标志数组和栈初始化。

数组全部设为0（未被访问状态）

②访问起始顶点，将这个顶点进栈，改变其访问标志。

③当栈不为空时循环，查找栈顶元素未被访问过的一个邻接顶点

如果栈顶元素找不到未被访问的邻接顶点，那么将栈顶元素出栈。

如果找到栈顶元素未被访问过的邻接顶点，那么访问该顶点，并将该顶点进栈，改变访问标志（改为1，表示

被访问过）。

以下mark的初始状态为0；

s是栈。起始为只有一个顶点（也就是1）

能找到未被访问过大 邻接结点是，一直进栈

找不到未被访问过的邻接顶点。一个一个栈顶元素出栈，直至为空。

算法：
x为起始顶点下标

以上都是基于连通图或者非连通图的连通分量来遍历实现的。

广度优先搜索：类似于树的层次遍历。

2、广度优先搜索的遍历序列：

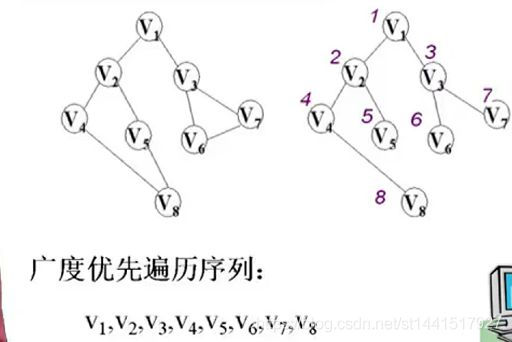
该序列也不是唯一的。

算法思想：

g是要遍历的图，v0是起始顶点。

此处需要创建一个队列Q；

访问起始顶点并且将起始顶点的标志设为1；

初始化一个队列，

将起始顶点入队，

只要队列不为空；

队列的首结点出队，然后寻找该顶点的邻接点，如果发现存在未被访问的邻接点的时候，访问该邻接点，然

后改变访问标志，接着将该顶点入队，

非递归算法：（邻接表存储结构）

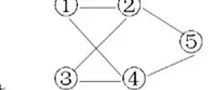
①标志数组和队列初始化

②访问起始顶点，入队。置已访问标志。

③当队列不为空时循环：查找队首元素未被访问过的所有邻接顶点。

若为找到，将当前队首元素出队；

若找到，访问该顶点，将该顶点入队，置已访问标志。

注意：此时的队首元素还没有被出队。所以可以继续访问该队首元素的其他邻接点，直至找不到出队为止；

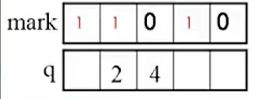
例如：1顶点为队首元素，访问完1顶点的2、4邻接顶点之后，将2、4顶点入队，接着，发现1顶点没有未被访

问过 的邻接顶点，所以1结点出队。

算法实现：

第一个for循环时初始起始顶点。

do{}while循环的条件是，队列不为空；f！=r

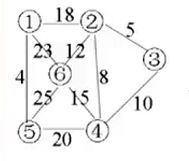
图应用算法之最小生成树：

假设从顶点1开始：

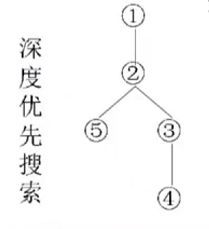
连通图或有根的有向图可以生成树；


意思是：之前的遍历算法输出的是顶点，现在改为输出的是两个顶点的操作（也就是边，因为两个顶点确定一条边）

特殊情况：

此时生成的是一个树林；
例如：


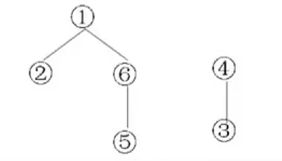
非连通图或者非强连通图生成树林的算法：

if中判断当前顶点是否被访问过。

此处调用的dfs函数中，应该将之前的输出顶点改为输出边。

此处注意：起始顶点不同，最后生成的树的个数可能是不同的；

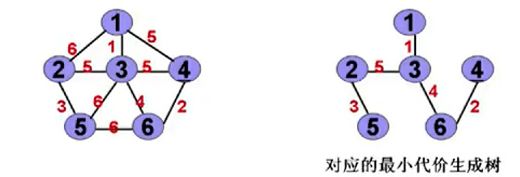
最小生成树

定义：生成树中边的权值（代价）之和最小的树。

此处：不要用肉眼描绘最小生成树，而是在之前生成的树林中边的权值之和最小的树。例如此处：

最小生成树的寻找方法：

找n-1条不构成回路的最小边。

两种常见算法：

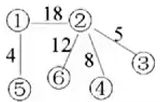
①Kruscal算法

先找权值最小的边，找到之和放在树中。

构建过程：


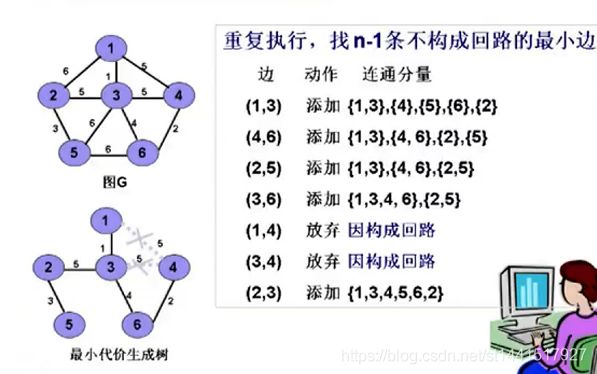
为什么U的初值等于V？是因为最小生成树的应该包含图所有的顶点。

i：顶点、j：顶点、w：权
对图中所有边进行排序（权值由小到大）

构建树：找最小边，且不会构成回路。

最后生成的结果：

②prim算法

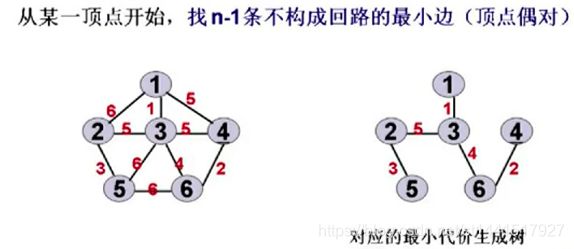
与之前的算法生成过程不同：

选取应该顶点放在树中：然后找以该顶点为起始点的边，找一个最小的边，对应就有一个新的结点加入到了

树中，此时也找出这个顶点为起始顶点的边。再寻找最小的边。

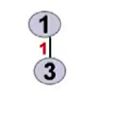
找出两个顶点的最小边：

因为此时（1,3）边已经进入树中，所以消除掉该边记录，接着找出以3为起始顶点的所有边，此时继续寻找发

现（1,2）边的权值比（3,2）边权值大，而且将（3，2）边放入树中不会发生回路，所以此时就可以将

（1,2）边删除掉，然后接着引入（3,6）边，这样子做的目的是为了减少查询次数。可以选择提前删除。

拓扑排序：
可以解决的问题：
AOV网络：用顶点边表示活动的网络。

顶点：一个工程中的活动。

边：活动的顶点间的优先关系。起点优于终点。

注意：AOV网中是不容许出现环的。

示例：

通俗说就是：干一件事之前，应该先把其他事干了，才能满足干这件事的条件。

先修关系：
AOV网

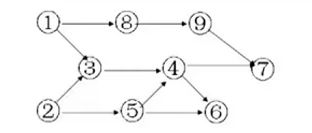
拓扑序列为：1, 8，9 ,2，5，3, 4，6, 7 序列不唯一

是前驱的一定在前面，但是在前面的不一定是前驱，例如9不是3的前驱一样。

进行拓扑排序的方法：

算法实现（邻接表的存储结构）

在存储结构中，需要多一个成员，记录该结点的入度，入度为0表示当前结点没有前驱。

使用一个存放入度为0的顶点的栈或者队列。只要出现入度为0的结点，就将其存入栈中。在选择起始点的时

候，可以直接在栈中寻找。

算法思想：

算法实现例子：


此时再栈中随意找一个顶点输出，因为此时都是入度为0的顶点，例如输出2，那么2出栈，此时将2后面的单

链表中的每个顶点的入度-1，如果出现为0的顶点，例如5此时的入度为0，那么5入栈，依次下去。直至栈为

空，终止此过程，现在的输出序列就是拓扑序列。

最短路径算法：

从图中某一个顶点（称为源点）到达另一顶点（称为终点）的路径可能不止一条，如何找到一条路径是的沿

此路径上各边的权值总和达到最小。

①（Dijkstra–单源最短路径问题）迪杰斯特拉

②（Floyd–所有顶点之间的最短路径）弗洛伊德

单源最短路径：

给定一个带权有向图和源点，从源点到图中其他顶点的最短路径（条件是各边上的权值大于或等于0）。

思想：按路径长度的递增次序，逐步产生最短路径。

步骤：首先求出长度最短的一条最短路径，在参照它求出长度次短的一条最短路径，以此类推，直到从顶点v

到其他各顶点的最短路径全部求出为止。

mark数组是标识该结点是否被访问过。没有为0，到达过为1；

源点是1，终点是dist终点元素。里面的每个元素下面对应的值都是从1结点开始无论是间接还是直接到达的路

径长度，并不是前驱到达的路径长度。

Path中存放的是顶点序列，也就是起点到达终点所要经过的顶点序列。起始顶点的初始状态为0，其他每个顶

点的初始状态都为1，也就是前驱暂且都认为是1。

注意：直接相连的顶点之间的这条路径不一定是最短的。

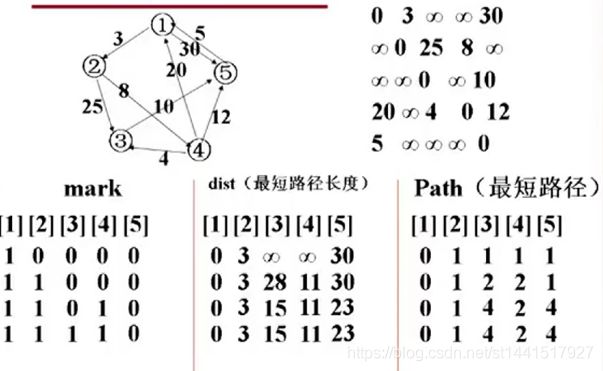
最短路径在dist中最下面一行存放，此处也就是：1到2长度为3，1到3长度是15,…。

到达的路径是在Path中最后一行存放。最短路径如下：

所有顶点之间的最短路径：

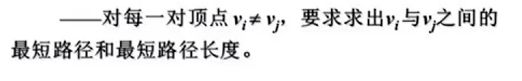
解决方法：

①将每一个顶点都作为源点，都使用一次迪杰斯特拉算法。

②Floyd算法。

借助邻接矩阵的初始状态。

M0初始状态就是这个图的邻接矩阵。

基本思想：递推地产生一个矩阵序列。


递推公式：

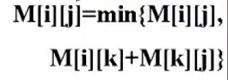
多少个顶点就递推出多少个矩阵，（不包含M0邻接矩阵）

i表行，j表列。i=k,j=k，i=j时的值不变，所以矩阵中的第一列和第一行还有对称轴都没有发生变化。

i和j的取值由当前矩阵中缺少元素的坐标决定的，k是当前矩阵的的序号。

红色标记是递推出的值，起初建立矩阵的时候这个位置没有值，是递推出的。

递推出的最后一个矩阵的元素坐标就是行号为起点，列号为终点的路径，路径长度是对应元素的值。

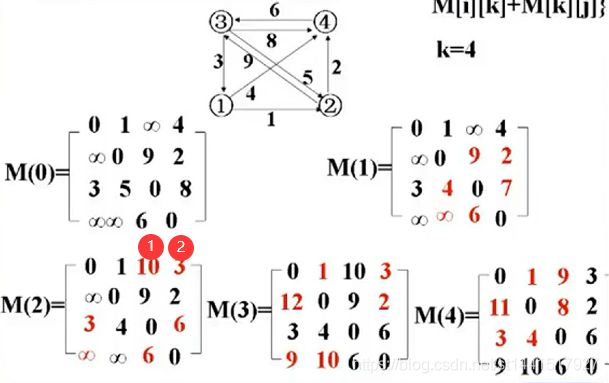
计算①时：i为1，j为3，k为2.

递推过程就是：M（1）矩阵中（1,3）位置的值（无穷大）和（1,2）位置的值（1）+（2,3）位置的值（9）

之和（10）中的最小取值（10）。

计算②时：i为1，j为4，k为2.

过程：M（1）矩阵中（1,4）位置的值（4）和（1,2）位置的值（1）+（2,4）位置的值（2）之和（3）中取

最小值，也就是（3）。

图的关键路径：

AOV网：用边表示活动的网络，有向无环图。

要解决的问题是：

（1）完成整个工程至少需要多少时间（假设网络中没有环）

（2）为缩短完成工程所需的时间，应当加快哪些活动？

顶点表示事件，边表示完成该事件需要的时间。

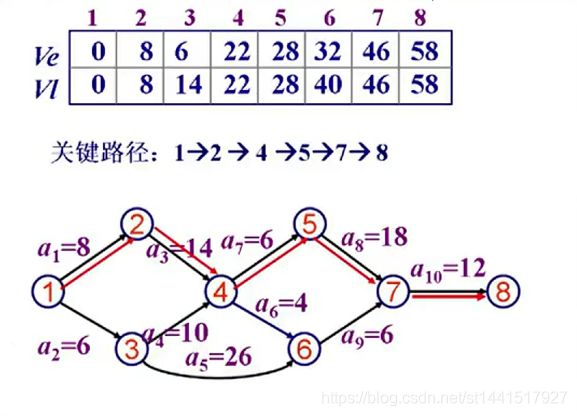
例如4：

最短开始时间：8+14=22,6+10=16，取值大的，因为需要满足两个条件才可以完成4，所以得取多的时间来保

证能够完成前提条件，所以4的最短开始时间是22.

最迟开始时间：倒着往回看，8的最长开始时间是58,7的是58-12=46,6的是46-6=40,5的是46-18=28,4的是28-4=24。

6=28,40-4=36,28小于36，所以是28.此处选取较短的时间为最迟开始时间。

最早开始时间和最晚开始时间相等的顶点是关键路径。

此处也就是：1-2-4-5-7-8；

求关键路径的方法：

定义一个队列：来存储入度为0的顶点，当没有结点的前驱是队首元素的时候，也就是当前队首元素的后继结

点全部已经在队列当中了，直接将队首元素出队。

定义一个数组longest：来存储到达该结点的最早开始时间，

定义一个数组pre：来存储当前结点的前驱结点。